微分可能物理学とは何か？

はじめに

昨今、微分可能物理学という用語を目にする機会が多くなってきました。

しかし、これが何を意味するのか、どのうような意義があるのかがはっきりと分かりません。 （実際、高校数学で習うような微分可能性の定義とは違うようです）

そこで、今回は、微分可能物理学が一体何なのかを調査してみました。

微分可能プログラミングと微分可能物理学

まず、微分可能プログラミングというものがあります。

この用語は、2017年か2018年頃に誕生した言葉とのことです。

深層学習のニューラルネットワークは、自動微分を行うライブラリ（Theano、TensorFlow、PyTorchなど）で記述することが多いです。 そうすると、ニューラルネットワークの学習過程は、自動微分を用いて計算した勾配で、ニューラルネットワークの重みを最適化していくことになります。 この自動微分で勾配を計算し最適化する対象を、ニューラルネットワーク以外に拡張したものが 微分可能プログラミングと呼ばれています。

そして、微分可能プログラミングの対象がレンダリングであれば、微分可能レンダリングとよばれ、 物理学であれば、微分可能物理学と呼ばれています。

また、物理シミュレーションにおいては、自動微分でなく、Adjoint法で勾配を計算して、最適化していく場合もありますが、 これらは微分可能物理学と同等なものと言えるでしょう。

しかし、まだ微分可能物理学が何なのかが分からないので、例を見てみましょう。

微分可能物理学の例

具体的には、微分可能物理学のプログラムはどのうようなものになるのでしょうか？

ここでは、DiffTaichiにある 「３つのばねと３つの質点からなる質量ばね」の例題(mass_spring_simple.py)を見てみましょう。

📌 DiffTaichiは、高性能な微分可能物理シミュレーターを構築するために開発された 微分可能プログラミング言語です。
順方向のシミュレーターに対して、最小限のコード変更で、自動微分シミューレーターを自動生成します。
また、並列化という観点では、Cudaで手作りしたときと同等の計算速度を得ることができます。

この例題は、微分可能物理シミュレーターを用いて最適化問題

3つのばねからなる三角形の面積が0.2になるような、３つのばねの自然長を求める

を解きます。

微分可能な質量ばねシミュレーターの構築

まず、DiffTaichiで、微分可能な質量ばねシミュレーターを構築します。

DiffTaichは、命令型のプログラミング言語なので、 FortranやC++で記述するようにシミュレーターのコードを記述できます。

• グローバル変数のメモリ割り当て

最初に、シミュレーションの状態を保存するためのグローバルテンソルにメモリを割り当てます。

scalar = lambda: ti.field(dtype=real)
vec = lambda: ti.Vector.field(2, dtype=real)

loss = scalar()
x = vec()
v = vec()
force = vec()

spring_anchor_a = ti.field(ti.i32)
spring_anchor_b = ti.field(ti.i32)
spring_length = scalar()

• カーネルの定義

次に、質量-ばね系をフックの法則でモデル化します。フックの法則は次式で表されます。

$$ \bf{F} = k(||\bf{x}_a - \bf{x}_b||_2 - \ell_0)\frac{\bf{x}_a - \bf{x}_b}{||\bf{x}_a - \bf{x}_b||_2} $$

ここで、$\bf{F}$はばね力、$\bf{x}_a, \bf{x}_b$は2質点の位置座標、$\ell_0$はばねの自然長です。

以下のカーネルは、すべてのばねをループし、力を質点に分散させています。

@ti.kernel
def apply_spring_force(t: ti.i32):
    # Kernels can have parameters. there t is a parameter with type int32.
    for i in range(n_springs):  # A parallel for, preferably on GPUs
        a, b = spring_anchor_a[i], spring_anchor_b[i]
        x_a, x_b = x[t - 1, a], x[t - 1, b]
        dist = x_a - x_b
        length = dist.norm() + 1e-4
        F = (length - spring_length[i]) * spring_stiffness * dist / length
        # apply spring impulses to mass points. Use atomic_add for parallel safety.
        ti.atomic_add(force[t, a], -F)
        ti.atomic_add(force[t, b], F)

続けて、各時間ステップ$t$における、各質点$i$の速度$v_{t,i}$と位置座標$x_{t,i}$を減衰つきの半陰解法オイラー時間積分で求めます。

$$ \bf{v}_{t,i} = e^{-\Delta t\alpha}\bf{v}_{t-1,i} + \frac{\Delta t}{m_i}\bf{F}_{t,i} $$

$$ \bf{x}_{t,i} = \bf{x}_{t-1,i} + \Delta t \bf{v}_{t,i} $$

ここで、$\alpha$は減衰定数です。カーネルは次のようになります。

@ti.kernel
def time_integrate(t: ti.i32):
    for i in range(n_objects):
        s = math.exp(-dt * damping)
        new_v = s * v[t - 1, i] + dt * force[t, i] / mass
        new_x = x[t - 1, i] + dt * new_v
        if new_x[0] > 0.4 and new_v[0] > 0:
            # friction projection
            if new_v[1] > 0:
                new_v[1] -= ti.min(new_v[1], friction * new_v[0])
            if new_v[1] < 0:
                new_v[1] += ti.min(-new_v[1], friction * new_v[0])
            new_v[0] = 0
        v[t, i] = new_v
        x[t, i] = new_x

• 順解析の関数

上で定義した、apply_spring_force、time_integrate関数をまとめて、順解析のforward関数を作ります。

def forward(output=None):
    for t in range(1, steps):
        apply_spring_force(t)
        time_integrate(t)

以上で、微分可能な質量ばねシミュレーター（すなわち、自動微分シミューレーター）が構築されました。

最適化

• 損失関数の定義

最適化問題を解くには、損失関数が必要です。

3つのばねからなる三角形の面積が0.2からどれだけ離れているかを損失関数として定義します。

@ti.kernel
def compute_loss(t: ti.i32):
    x01 = x[t, 0] - x[t, 1]
    x02 = x[t, 0] - x[t, 2]
    area = ti.abs(
        0.5 * (x01[0] * x02[1] - x01[1] * x02[0]))  # area from cross product
    target_area = 0.2
    loss[None] = (area - target_area)**2

• メイン関数

最後に、メイン関数です。

def main():
    for iter in range(80):
        with ti.Tape(loss):
            forward()
            compute_loss(steps - 1)

        print('Iter=', iter, 'Loss=', loss[None])

        for i in range(n_springs):
            spring_length[i] -= learning_rate * spring_length.grad[i]

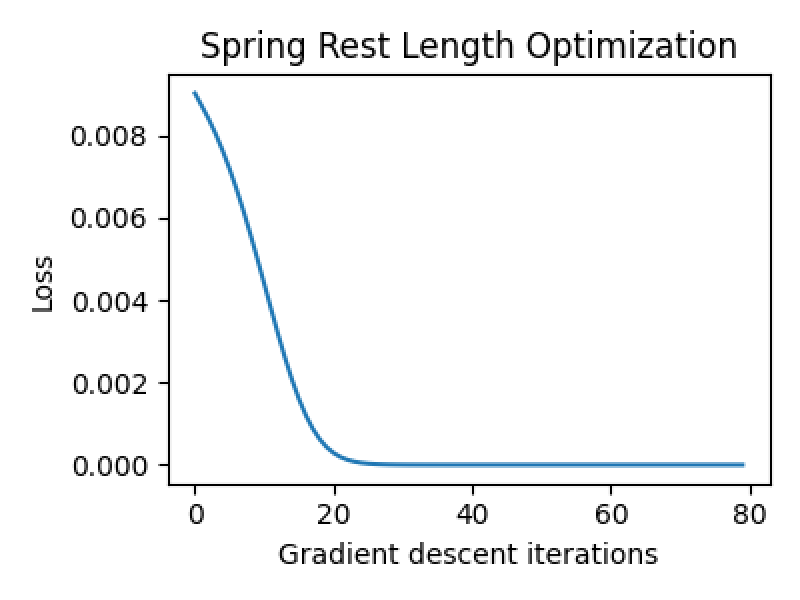
初期の自然長を[0.1, 0.1, 0.14]として、上のメイン関数を実行すると、最終的なばねの自然長は[0.66, 0.76, 0.70]となり、 三角形の面積もターゲットの0.2になりました。

下図は、繰り返し毎の損失のグラフで、ゼロに漸近しています。

繰り返し毎の損失のグラフ

下の動画は、繰返し毎に、ばねの自然長が広がっていき、面積がターゲットの0.2に近づいていく様子を示しています。

以上から、微分可能物理学がどんなものかが分かってきます。

つまり、自動微分が組み込まれた物理シミュレーター（解析ソルバー）を使用すると、勾配を計算できるので、 最急勾配法で最適化ができるというのが、微分可能物理学と呼ばれているもののようです。

汎用ソルバーを微分可能物理学にするには？

それでは、ANSYS FluentやOpenFOAMのような 汎用ソルバーを使用している方が、微分可能物理学を行うにはどうしたらよいでしょうか？

まず、微分可能な物理シミュレーターが必要です。しかし、 これら汎用ソルバーをDiffTaichiやJAXを用いて、書き直すのは困難でしょう。

それでは、汎用ソルバーを微分可能物理学にするのは不可能なのでしょうか？

実は、ニューラルネットワークと物理シミュレーターを組み合わせることで、 近似的に汎用ソルバーを微分可能物理シミューレーターのように扱うことができます。

例えば、Reducing Numerical Errors with Deep Learning に、その例を見ることができます(Google Colabで実際に動かすこともできます）。

この例では、離散化誤差をニューラルネットワークに学習させて、解析ソルバーの解を補正することで、 使用したメッシュの解像度よりも高解像度の計算結果を得ることができます。

おわりに

本記事では、微分可能物理学について、調査し、微分可能物理学がどんなものかを少し分かった気がします。

汎用ソルバーを微分可能物理学にする節でも見たように、 微分可能物理学では、深層学習と従来からあるソルバーを組み合わせる例が多く見られます。 こうすることで、汎用ソルバーを大幅に上回る性能を発揮する可能性があるとのことです。

このように、深層学習で物理シミュレーションを置き替えようとするサロゲートモデルとは異なり、 従来の物理シミュレーションと深層学習が共存して、 高い性能を発揮する方向を目指しているのは興味深いです。

一方、微分可能物理学と立場が対極にあるサロゲートモデルも進展が見られます。 2021年にDeepMindが発表したMeshGraphNetsの論文 Learning Mesh-Based Simulation with Graph Networks では、学習データやGNN(Graph Neural Network)層、MLP(Multilayer Perceptron）を 増やしていけば、99.98%の精度のサロゲートモデルを得ることができると主張しています。

いずれにしても、深層学習と物理シミュレーションの関係が今後、どうなっていくかは興味深いですね。

• differentiable
• difftaichi