静止液滴形状の理論解

概要

水平面上に置かれた静止液滴の形状を理論的に導く興味深い方法を紹介する。 ここで説明する手法の元の参照論文は以下である。

Thermodynamics of Sessile Drops on a Rigid Substrate: A Comparison of Two Theories

この手法では、静止液滴は表面張力エネルギと重力による位置エネルギーの和が最小になるように形状が決まるとして変分方程式を導く。

その後液滴の体積が規定されている場合を想定し、ラグランジ未定乗数法を使い、オイラーラグランジ方程式を求める。

この定式化によれば、最終的に得られた微分方程式は表面張力と重力の釣り合いを表す方程式になること、 またラグランジ未定乗数は液滴最下点での曲率(表面張力)を表現していることが分かった。

またjuliaコードを使った数値解析により液滴形状を再現することができた。

理論解の導出

水平の平板上に液滴が静止している場合を考える。

液滴の形状は液滴の物性値、液体-気体-固体の接触角、重力などの影響を受ける。

ここではある指定された体積の液滴が平板上に置かれた場合の形状を理論的に導いた。

解析対象

下図に示すような液滴形状を考える。

液滴は中心軸周りの回転対称となっているため軸対称場として形状を求める。

液滴形状は球座標系を用いて表現した。この場合、$R(\theta)$を求めることが目標となる。

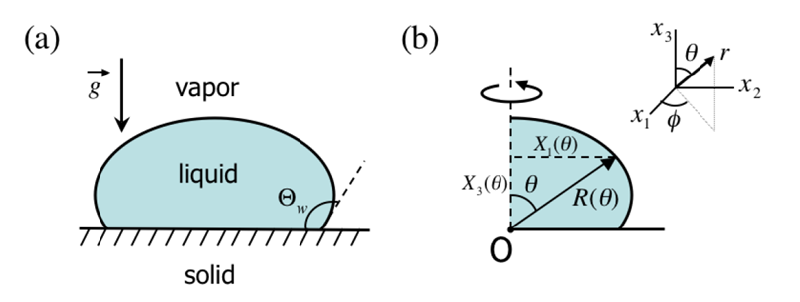
接触角

固体基板と液滴の接触点では Young-Dupreの式が成り立つ。

$$ \begin{align} \cos \Theta_w &= \frac{\gamma_{sv}-\gamma_{ls}}{\gamma_{lv}} \end{align} $$

ここで、$\gamma_{lv}$は、液相-気相間の表面自由エネルギ、$\gamma_{ls}$は、液相-固相間の表面自由エネルギ、$\gamma_{sv}$は、固相-気相間の表面自由エネルギである。

平衡状態では表面エネルギが最小となっており、状態の微小変化に対して次式が成り立つ。

$$ \begin{align} \delta G = \delta(\gamma_{lv} A_{lv}+\gamma_{sv} A_{sv}+\gamma_{ls} A_{ls}) \ge 0 \end{align} $$

ここで$G$は熱力学的ポテンシャルである。

元論文の著者はこの式を直接使わないで、全表面エネルギーを別の表現式で表した。

$$ \begin{align} \delta G = \delta(\gamma_{lv} A_{lv}+(\gamma_{lv}+\lambda_l) A_{ls}) \ge 0 \end{align} $$

これは表面エネルギを液相-固相間の接触面積$A_{ls}$の線形関数として表すものであり、実際には

$$ \begin{align} \lambda_l = (\gamma_{ls} - \gamma_{sv}) - \gamma_{lv} \end{align} $$

であることが後で説明される。

表面張力によるエネルギー

表面張力によるエネルギ$G_i$は次式で表される。

ここでドット記号は、$\theta$に関する微分を表している。

$$ \begin{align} G_i &= \pi(\gamma_{lv}+\lambda_l) X_1\left(\frac{\pi}{2}\right)^2 +2\pi\gamma_{lv}\int_0^{\pi/2} X_1(\theta)\sqrt{\dot{X}_1(\theta)^2+\dot{X}_3(\theta)^2} d\theta \notag \\ \end{align} $$

$$ \begin{align} &= \pi(\gamma_{lv}+\lambda_l) R\left(\frac{\pi}{2}\right)^2 +2\pi\gamma_{lv}\int_0^{\pi/2} R(\theta)\sqrt{\dot{R}(\theta)^2+R(\theta)^2}\sin(\theta) d\theta \end{align} $$

なおここでは以下に示すデカルト座標系と球座標系の変換式を使用した。

$$ \begin{align} X_1 = R \sin(\theta), \quad \dot{X}_1 = \dot{R}\sin(\theta)+R\cos(\theta) \notag \\ X_3 = R \cos(\theta), \quad \dot{X}_3 = \dot{R}\cos(\theta)-R\sin(\theta) \notag \end{align} $$

重力による位置エネルギ

重力による位置エネルギ$G_g$は次式で表される。

$$ \begin{align} G_g &= \rho g \int_V X_3 dV = \int_0^{2\pi} d\phi \int_0^{\pi/2} \sin(\theta)\cos(\theta) d\theta \int_0^{R(\theta)}R^3 dR \notag \\ &= \frac{\pi}{2}\rho g \int_0^{\pi/2} R(\theta)^4 \cos(\theta)\sin(\theta) d\theta \end{align} $$

全エネルギ

全エネルギ$G$は表面張力エネルギと位置エネルギの合計$(=G_i+G_g)$で表される。

$$ \begin{align} G &= \pi(\gamma_{lv}+\lambda_l) R\left(\frac{\pi}{2}\right)^2 \\ &+\pi\int_0^{\pi/2} \left[2\gamma_{lv}R\sqrt{\dot{R}^2+R^2} + \frac{\rho g}{2} R^4 \cos\theta \right] \sin\theta d\theta \end{align} $$

ここで$R$は$\theta$の関数となっており、全エネルギーが最小となるような$R(\theta)$を求めることが目的である。

変分法では全エネルギーが最小となる条件を求める。

無次元化

全エネルギー式を$\gamma_{lv}L^2$で割り無次元化する。

ここで$L$は代表長さ、$\gamma_{lv}$は、気液間の表面張力係数である（$L$の決定法については後述）。

$*$付きの変数は無次元化された変数を表している。

$$ \begin{align} G^\ast(R^\ast,\dot{R}^\ast) &= \pi(1+\alpha) R^*\left(\frac{\pi}{2}\right)^2 \\ &+\pi\int_0^{\pi/2} \left[2R^\ast\sqrt{\dot{R}^{\ast 2}+R^{\ast 2}}+\frac{\beta}{2} R^{*4} \cos\theta \right] \sin\theta d\theta \end{align} $$

ここで、$\alpha, \beta$は無次元パラメータであり、以下のように定義される。

$$ \begin{align} \alpha&=\frac{\lambda_l}{\gamma_{lv}} \notag \\ \beta&=\frac{\rho g L^2}{\gamma_{lv}} \notag \end{align} $$

液滴の体積

液滴体積$V$が規定されている場合を考える。$V$は次式で表される。

$$ \begin{align} V = \frac{2\pi}{3}\int_0^{\pi/2} R^3 \sin\theta d\theta \end{align} $$

代表長さ$L$を$V$に基づき$L=V^{1/3}$と定義する。

この場合、液滴体積の表現式の両辺を$L^3$で割って無次元化すると以下のようになる。

$$ \begin{align} V^* = \frac{2\pi}{3}\int_0^{\pi/2} R^{*3} \sin\theta d\theta = 1 \end{align} $$

ラグランジ未定乗数法

液滴の体積を拘束条件式として記述すると以下のようになる。

$$ \begin{align} H^\ast(R^\ast) &= V^\ast -1 = \frac{2\pi}{3}\int_0^{\pi/2} R^{\ast 3} \sin\theta d\theta - 1 = 0 \end{align} $$

この拘束条件をラグランジ未定乗数法を使って表す。

$$ \begin{align} I^* &= G^\ast(R^\ast,\dot{R}^\ast) - \eta H^\ast(R^\ast) \notag \\ & = \pi(1+\alpha) R^\ast\left(\frac{\pi}{2}\right)^2 \notag \\ & \quad +\pi\int_0^{\pi/2} \left[2R^\ast\sqrt{\dot{R}^{\ast2}+R^{\ast2}} + \frac{\beta}{2} R^{\ast4} \cos\theta \right] \sin\theta d\theta \notag \\ & \quad - \eta \left( \frac{2\pi}{3}\int_0^{\pi/2} R^{\ast3} \sin\theta d\theta - 1 \right) \notag \\ & = \pi(1+\alpha) R^\ast\left(\frac{\pi}{2}\right)^2 \notag \\ & \quad +\pi\int_0^{\pi/2} \left[2R^\ast\sqrt{\dot{R}^{\ast2}+R^{\ast2}} + \frac{\beta}{2} R^{\ast4} \cos\theta - \frac{2}{3}\eta R^{\ast3} \right] \sin\theta d\theta + \eta \end{align} $$

ここで$\eta$はラグランジの未定乗数であり、(12)式を制約なしの最小化問題として解を求めればよい。

以下では記述を簡略化するために無次元量を表す$*$を省略する。

また(12)式を定数$\pi$で割って簡略化する。

$\theta$の任意関数を$\zeta(\theta)$とし、変分を取るために比較関数$R_\epsilon(\theta)$を次式で表す。

$$ \begin{align} R_\epsilon(\theta) = R(\theta)+\epsilon\zeta(\theta) \end{align} $$

比較関数を(12)式に代入し、第一変分がゼロとなる条件を求める。

$$ \begin{align} \frac{\partial I(\epsilon)}{\partial \epsilon} &= 2(1+\alpha) R\left(\frac{\pi}{2}\right)\zeta(\frac{\pi}{2}) \notag \\ & \quad +\int_0^{\pi/2} \zeta \frac{\partial}{\partial R_\epsilon}\left[\left(2R_\epsilon \sqrt{\dot{R}_\epsilon^2+R_\epsilon^2} + \frac{\beta}{2} R_\epsilon^4 \cos\theta - \frac{2}{3}\eta R_\epsilon^3 \right) \sin\theta \right] \notag \\ & \quad +\dot{\zeta} \frac{\partial}{\partial \dot{R}_\epsilon}\left[\left(2R_\epsilon\sqrt{\dot{R}_\epsilon^2+R_\epsilon^2} + \frac{\beta}{2} R_\epsilon^4 \cos\theta - \frac{2}{3}\eta R_\epsilon^3 \right)\sin\theta \right] d\theta \notag \\ &= 2(1+\alpha) R\left(\frac{\pi}{2}\right)\zeta(\frac{\pi}{2}) \notag \\ & \quad +\int_0^{\pi/2} \zeta \left[ 2\sin\theta\left( \frac{2R^2+\dot{R}^2}{\sqrt{\dot{R}^2+R^2}} +\beta R^3 \cos\theta - \eta R^2\right)\right] \notag \\ & \quad +\dot{\zeta} \left[ 2\sin\theta \frac{R \dot{R}}{\sqrt{\dot{R}^2+R^2}} \right] d\theta \notag \\ &= 2(1+\alpha) R\left(\frac{\pi}{2}\right)\zeta(\frac{\pi}{2}) \notag \\ & \quad +\int_0^{\pi/2} \zeta \left[ 2\sin\theta\left( \frac{2R^2+\dot{R}^2}{\sqrt{\dot{R}^2+R^2}} +\beta R^3 \cos\theta - \eta R^2\right) -\frac{d}{d \theta} \left(2\sin\theta \frac{R \dot{R}}{\sqrt{\dot{R}^2+R^2}} \right)\right] d \theta \notag \\ & \quad + \zeta\left(\frac{\pi}{2}\right) \left( 2\sin\left(\frac{\pi}{2}\right) \frac{R\left(\frac{\pi}{2}\right) \dot{R}\left(\frac{\pi}{2}\right)}{\sqrt{\dot{R}\left(\frac{\pi}{2}\right)^2+R\left(\frac{\pi}{2}\right)^2}} \right) -\zeta\left(0\right) \left( 2\sin\left(0\right) \frac{R\left(0\right) \dot{R}\left(0\right)}{\sqrt{\dot{R}\left(0\right)^2+R\left(0\right)^2}} \right) \notag \\ &=\int_0^{\pi/2} \zeta \cdot 2\sin\theta R^2\left[\left(\frac{2\dot{R}^2+R^2-\ddot{R}R}{\left(\dot{R}^2+R^2\right)^{3/2}} \notag \\ +\frac{R-\dot{R}\cot\theta}{R\sqrt{\dot{R}^2+R^2}} \right) +\beta R \cos\theta-\eta \right] d \theta \notag \\ & \quad + \zeta\left(\frac{\pi}{2}\right) \left( 2(1+\alpha) R\left(\frac{\pi}{2}\right)+2\sin\left(\frac{\pi}{2}\right) \frac{R\left(\frac{\pi}{2}\right) \dot{R}\left(\frac{\pi}{2}\right)}{\sqrt{\dot{R}\left(\frac{\pi}{2}\right)^2+R\left(\frac{\pi}{2}\right)^2}} \right) \notag \\ & \quad - \zeta\left(0\right) \left( 2\sin\left(0\right) \frac{R\left(0\right) \dot{R}\left(0\right)}{\sqrt{\dot{R}\left(0\right)^2+R\left(0\right)^2}} \right) =0 \end{align} $$

この式が任意の$\zeta$に対して成り立つためには、以下の3式が成り立つことが必要である。

これらの式を解くことで液滴形状を得ることができる。

(15),(16)式は境界条件式、(17)が実際に解くべき微分方程式を表している。

$$ \begin{align} 2\sin\left(0\right) \frac{R\left(0\right) \dot{R}\left(0\right)}{\sqrt{\dot{R}\left(0\right)^2+R\left(0\right)^2}} = 0 \\ R\left(\frac{\pi}{2}\right) \left[ (1+\alpha) +\sin\left(\frac{\pi}{2}\right)\frac{ \dot{R}\left(\frac{\pi}{2}\right)}{\sqrt{\dot{R}\left(\frac{\pi}{2}\right)^2+R\left(\frac{\pi}{2}\right)^2}} \right] =0 \\ \left[ \frac{2\dot{R}^2+R^2-\ddot{R}R}{\left(\dot{R}^2+R^2\right)^{3/2}} \\ +\frac{R-\dot{R}\cot\theta}{R\sqrt{\dot{R}^2+R^2}} \right] +\beta R \cos\theta=\eta \end{align} $$

得られた微分方程式(17)に注目してみると、左辺の大括弧で囲んだ部分は、 実は液面の曲率(すなわち表面張力)に等しい（微分幾何学の公式から導くことができる）。

一方左辺第二項($\beta$を含む項)は重力項を無次元化した項になっている。

すなわち(17)式は作用力の釣り合いを記述している。

これからラグランジ未定乗数$\eta$の物理的な意味づけを導くことができる。

$\theta=\pi/2$とすると左辺第二項はゼロになるため、 ラグランジ未定乗数$\eta$は固体壁面上における液滴表面の曲率(表面張力)を表している ことがわかる。

境界条件

液滴の頂点($\theta=0$)および最下点($\theta=\pi/2$)では以下の関係が成り立つ。

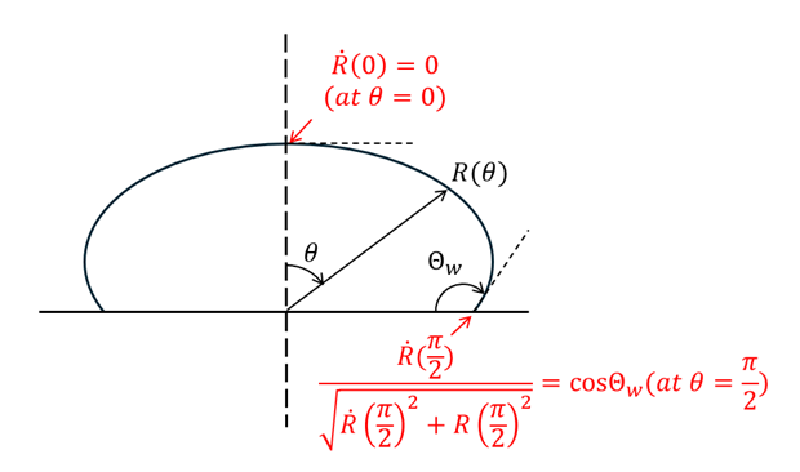
• 液滴の頂点（$\theta=0$ ）では液滴表面は水平であることから

$$ \begin{align} \dot{R}(0)=0 \end{align} $$

• 液滴最下点（$\theta=\pi/2$）では接触角が指定されることから

$$ \begin{align} \frac{\dot{R}\left(\frac{\pi}{2}\right)}{\sqrt{\dot{R}\left(\frac{\pi}{2}\right)^2+R\left(\frac{\pi}{2}\right)^2}} = \cos\Theta_w \end{align} $$

なお、接触角が上式で表されることは以下の図で説明できる。

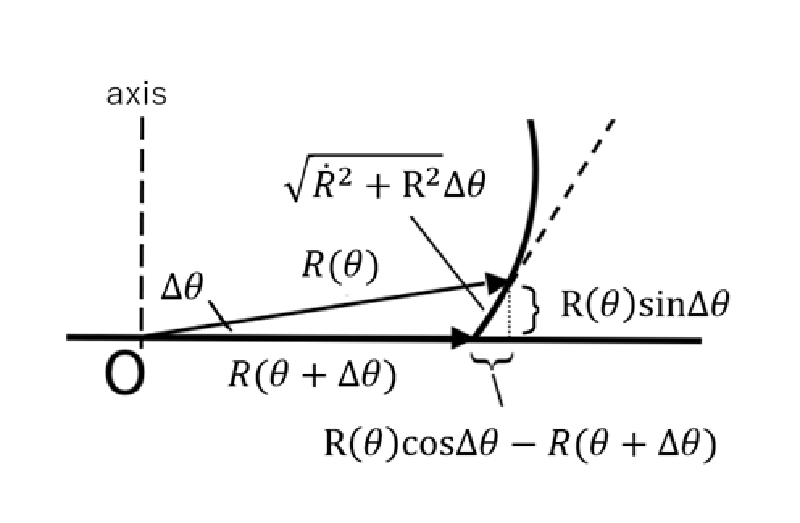
先に述べた(15)式と(16)式の関係について調べてみる。

(15)式については$\sin(0)=0$であることから$\dot{R(0)}$は任意の値を取ることができ、(18)式は自動的に成り立っていると考えられる。

一方(16)式については、$R\left(\frac{\pi}{2}\right)\ne0$であることから

$$ \begin{align} (1+\alpha)+\frac{\dot{R}\left(\frac{\pi}{2}\right)}{\sqrt{\dot{R}\left(\frac{\pi}{2}\right)^2+R\left(\frac{\pi}{2}\right)^2}} = 0 \end{align} $$

あるいは

$$ \begin{align} \dot{R}\left(\frac{\pi}{2}\right) =-(1+\alpha)\sqrt{\dot{R}\left(\frac{\pi}{2}\right)^2+R\left(\frac{\pi}{2}\right)^2} \end{align} $$

となる。$\dot{R}\left(\frac{\pi}{2}\right)$について解くと

$$ \begin{align} \dot{R}\left(\frac{\pi}{2}\right) = \pm \frac{(1+\alpha)R\left(\frac{\pi}{2}\right)}{\sqrt{-(2\alpha+\alpha^2)}} \end{align} $$

右辺の分母の根号内が正であるためには、$-2<\alpha<0$であることが必要であり、有次元値で表現すると以下のようになる。

$$ \begin{align} -2\gamma_{lv}<\lambda_l<0 \end{align} $$

(20)式より

$$ \begin{align} \cos\Theta_w = -(1+\alpha) \end{align} $$

となり$\alpha$の定義式を代入すると

$$ \begin{align} \gamma_{lv}\cos\Theta_w = -(\gamma_{lv}+\lambda_l)=\gamma_{sv}-\gamma_{ls} \end{align} $$

従って$\lambda_l$を以下のように定義すれば自動的に(16)式は成り立つことがわかる。

$$ \begin{align} \lambda_l = (\gamma_{ls}-\gamma_{sv}) - \gamma_{lv} \end{align} $$

この$\lambda_l$を(23)式に代入すると、等価な次式が得られる。

$$ \begin{align} -1<\cos \Theta_w <1 \end{align} $$

数値計算

液滴形状を表す方程式((17)式)は二階の常微分方程式になっている。

これを連立一階常微分方程式に変換して解を求める。

対象とする問題を再記すると以下のようになる。

なお、元論文では$\theta=0$において、微分方程式が特異になるとして、 球座標系ではなく円筒座標系に変換した微分方程式を使っているが、 ここでは球座標系の微分方程式をそのまま使用する。

ただし $\theta=0$においては液滴頂点曲率を使用するようにした。

なおここで微係数$d/dt$の$t$は角度$\theta$の意味であることに注意。

微分方程式

$$ \begin{align} \frac{d R}{d t} &= Q \\ \frac{d Q}{d t} &= \frac{1}{R}\left[ \left(Q^2+R^2\right)^{3/2}{ \frac{R-Q\cot(\theta)}{R\sqrt{Q^2+R^2}} +\beta R \cos(\theta)-\eta }+R^2+2Q^2 \right] \quad (when \quad \theta>\epsilon) \notag \\ &= R - \frac{R^2}{2}(\eta - \beta R ) \quad (when \quad otherwise) \end{align} $$

ここで$\epsilon$は微小数（計算機イプシロン）である。

境界条件

境界条件は積分区間の両端で与えられており、二点境界値問題として計算することになる。

$$ \begin{align} & \dot{R}(0) =Q(0)=0 \\ & \frac{\dot{R}\left(\frac{\pi}{2}\right)}{\sqrt{\dot{R}\left(\frac{\pi}{2}\right)^2+R\left(\frac{\pi}{2}\right)^2}} = \frac{Q\left(\frac{\pi}{2}\right)}{\sqrt{Q\left(\frac{\pi}{2}\right)^2+R\left(\frac{\pi}{2}\right)^2}} = \cos \Theta_w \end{align} $$

解析例

流体が水で、接触角が45,90,135[deg]の３ケースについて計算を行ってみた。

計算に使用したパラメータは、以下の通りである。

• 流体密度: $\rho=1000[kg/m^3]$
• 表面張力係数: $\gamma_{lv}=72.2[mJ/m^2]$
• 重力加速度: $g=9.8[m/s^2]$
• 液滴体積: $V=1[mL]=10^{-6}[m^3]$

最終的に得られた液滴形状を以下に示す。

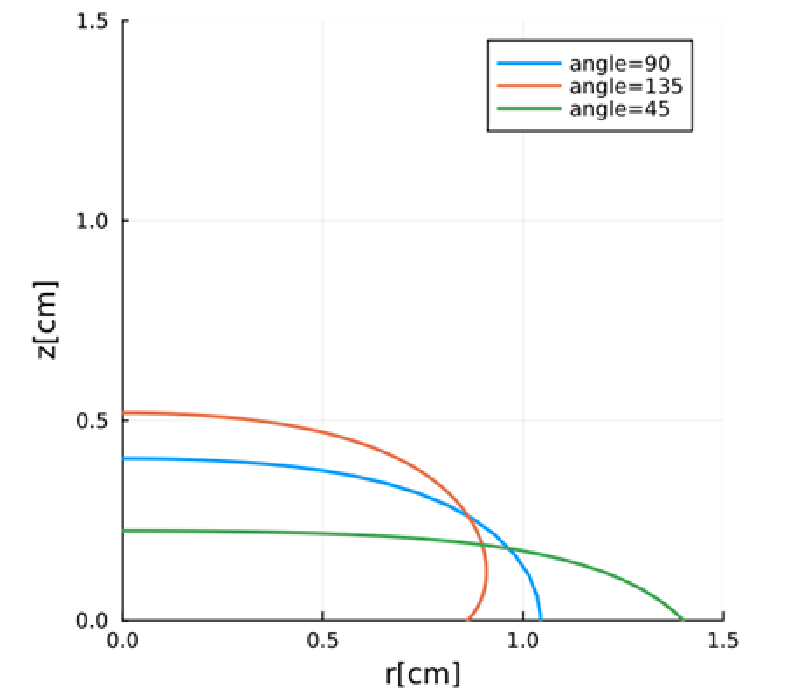
解析に使用したコード

以下に解析に使用したjuliaコードを示す。

ここでは、求解法として狙い撃ち法(shooting method)を使用した。

ここで示したコードは接触角$\Theta=90[deg]$の場合に対するものである。

$\beta,\eta,R_{ini}$の値を徐々に更新して、最終的に$\beta=13.57$、液滴体積$V=1.0$となるようにパラメータを調整した。

このケースでは$R_{ini}=0.4048,\eta=5.8904$で収束解が得られた。

using CSV, DataFrames, Roots, DifferentialEquations, Interpolations

#           R      Q
#u0_fun = [1.0, 0.0]  # initial run
u0_fun = [0.4048, 0.0]  # final run

tspan = (0.0, pi/2)

#beta, eta, theta = 0.0, 2.0, 90*pi/180  # initial run
beta, eta, theta = 13.57, 5.890399852497198, 90*pi/180  # final run
params = (beta, eta)

function droplet!(du,u,p,t)
    R, Q = u
    beta, eta = p
    du[1] = Q
    du[2] = ifelse(t < eps(),
        R - 0.5*R^2*(eta - beta*R),
        1/R*((Q^2 + R^2)^1.5
               * ((R - Q/tan(t))/(R*sqrt(Q^2 + R^2)) + beta*R*cos(t) - eta)
           + R^2 + 2*Q^2)
           )
end

function shooting_error(eta_guess)
    p = [beta, eta_guess]
    prob = ODEProblem(droplet!, u0_fun, tspan, p)
    sol = solve(prob, Tsit5(), abstol=1e-8, reltol=1e-8)

    Rf, Qf = sol(pi/2)
    target = cos(theta) * sqrt(Rf^2 + Qf^2)
    return target - Qf
end

function compute_vol(Rθ::Vector{Float64}, thetas::Vector{Float64})
    volume = 0.0
    R_interp = LinearInterpolation(thetas, Rθ)

    for i in eachindex(thetas)
        θ1 = thetas[i]
	θ0 = ( i==1 ? 0 : thetas[i-1] )
        dθ = θ1 - θ0
	θ = 0.5*(θ1 + θ0)
	R = R_interp(θ)
        volume += (1/3) * R^3 * sin(θ) * dθ
    end

    return 2π * volume
end

eta_solution = find_zero(shooting_error, (0.0, 10.0), Bisection())

p = [beta, eta_solution]
prob = ODEProblem(droplet!, u0_fun, tspan, p)
sol = solve(prob, Vern7(), abstol=1e-8, reltol=1e-8)

if sol.retcode == ReturnCode.Success
    println("? 計算は正常に収束しました")
    t = sol.t
    R = [u[1] for u in sol.u]  # R(t)
    Q = [u[2] for u in sol.u]  # Q(t)
    df = DataFrame(theta = t, R = R, Q = Q)
    CSV.write("droplet_solution.csv", df)
    println("eta_solution = $eta_solution")
    vol = compute_vol(df.R, df.theta)
    println("vol = $vol")

else
    println("? 解は収束しませんでした")
end

まとめ

平板上に置かれた静止液滴の形状の理論解を導いた。

液滴の全エネルギ（表面張力＋位置）を最小化するように変分方程式を定式化し、液滴体積はラグランジ未定乗数を使い拘束条件として与えた。

数値解析の結果妥当な計算結果が得られた。

弊社の解析事例

弊社の流体解析事例については、下記のリンクからご覧ください．

👉 解析事例のご紹介 FLUENT

👉 流体解析 実績及び事例

• 液滴
• fluent
• julia