平滑面摩擦
By Y.Sasaki
はじめに
地球温暖化への影響や化石燃料の枯渇問題への対応のためエネルギー効率の更なる向上が求められており、 航空・船舶・自動車などの移動体の抵抗低減が進んでいます。
物体に作用する全抵抗のうち、航空機では40%、船舶は80%、自動車は10%程度が物体表面の摩擦による抵抗と言われており、 この摩擦抵抗を低減することでエネルギー効率を改善することが可能になります。
今回は、CFDによる平滑面の摩擦力を事例として紹介します。
Deanによる摩擦係数の評価式
平行平板間な平滑面の乱流による摩擦係数は、Deanの摩擦係数評価式と比較しています。
$$ C_f = 0.073 Re^{\frac{1}{4}} $$
ここで、
- $Re$ : レイノルズ数は平板間の距離と平均流速
CFDによる摩擦係数の評価式
CFDによる計算では以下の式で摩擦係数を算出しています。
$$ C_{fCFD} = \frac{\tau w}{0.5\cdot \rho \cdot U_0^2} $$
ここで、
- $\tau w$：壁面せん断力
- $\rho$：流体密度
- $U_0$：境界層外側の主流速度
計算条件
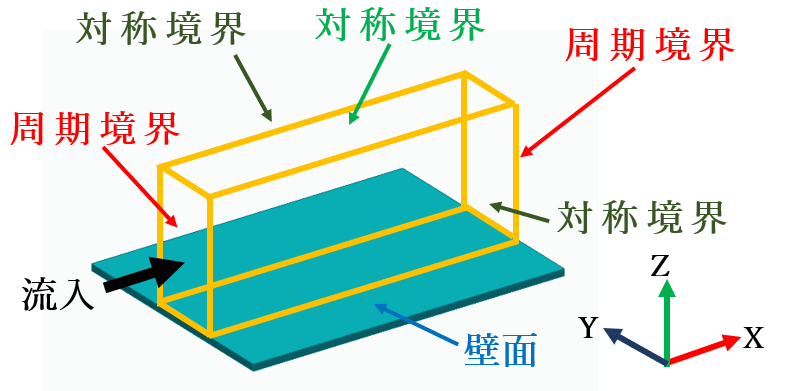
この事例では、摩擦力評価モデル図で示す計算領域を設定し壁面に作用する摩擦力を評価しています。
摩擦力評価モデル図
計算条件は以下の通りです。
- 流体：水
- 温度：20.0℃
- 粘性係数：$1.0014\times 10^{-3} Pa\cdot s$
- 密度：998.16 $kg/m^3$
- 流入：$Re = 1.0\times 10^1$ ～ $3.0\times 10^6$の８つの流速条件を定義
- 壁面：滑りなし
- 領域：
- X方向：周期条件
- Y方向：対称条件
- Z方向：対称条件
結果
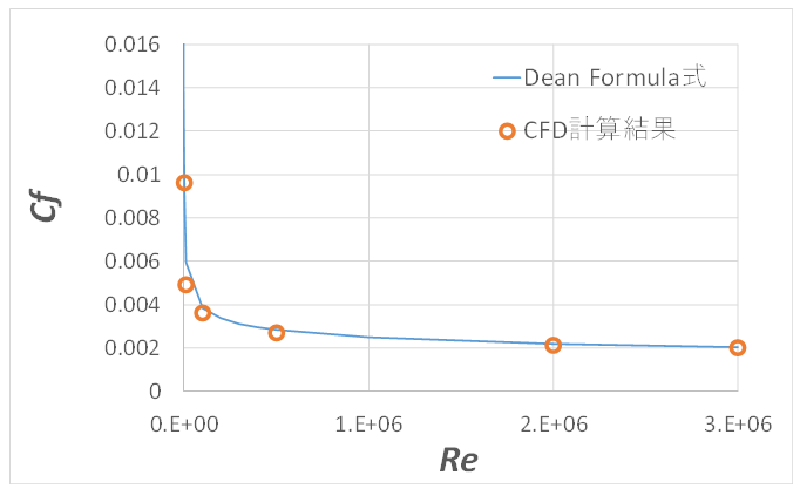
CFDで求めた壁面摩擦係数をDeanの評価式と比較したグラフを以下に示します。
$Re=1.0\times 10^1$ ～ $3.0\times 10^6$までの層流から乱流までの範囲で良好に一致していることが分かります。
各Reでの壁面摩擦係数
今後は、粗面や空力装置を用いた流れ制御による摩擦力の評価も事例として紹介する予定です。
弊社の解析事例
弊社の流体解析事例については、下記のリンクからご覧ください．