藤井聡太8冠の出現確率の一推定
By K.Yoshimi, 監修 N.Kumai,
はじめに
本記事では、藤井聡太8冠という極めて稀な存在を現在、目撃している状況下において、 このようなことがいかほど稀かを確認するために、藤井聡太8冠の出現確率を推定してみました。
藤井聡太8冠の推定レーティング値
まず、下表の藤井8冠の直近30対局の成績表(2023.11.10現在)は御覧のように、ほとんど無敵の状態を誇っています。
ここでは、レーティングのデータ(2023.11.10現在, http://kishibetsu.com/rating.html) を用いて、棋士としてピークであることが多い満26歳におけるレーティングを推定します。
推定方法は、この藤井8冠の直近30対局の成績表を用います。
- 藤井8冠の直近30対局の成績表
| 対戦相手のレーティング | 勝敗 |
|---|---|
| 1852 | ⚪ |
| 1863 | ⚪ |
| 1945 | ⚪ |
| 1863 | ⚪ |
| 1945 | ⚪ |
| 1863 | ⚪ |
| 1945 | ⚪ |
| 1945 | ⚪ |
| 1878 | ⚪ |
| 1672 | ⚪ |
| 1945 | ❌ |
| 1862 | ⚪ |
| 1862 | ❌ |
| 1915 | ⚪ |
| 1862 | ⚪ |
| 1862 | ⚪ |
| 1862 | ⚪ |
| 1862 | ⚪ |
| 1862 | ⚪ |
| 1852 | ⚪ |
| 1862 | ❌ |
| 1584 | ⚪ |
| 1862 | ⚪ |
| 1831 | ⚪ |
| 1878 | ⚪ |
| 1831 | ⚪ |
| 1831 | ❌ |
| 1547 | ⚪ |
| 1878 | ⚪ |
| 1831 | ⚪ |
- 推定手順は、以下のようにして行いました (下のManim CEで作成した動画を参照ください)。
-
藤井8冠の初期レーティングを設定:
ra = 2118(2023年11月10現在) -
トライアル・ループ:
M回2.1 直近30対局の成績表から、
N対局をランダム(重複あり)に抽出するループ-
2.1.1 抽出した1対局から下記変数を設定
- 対戦相手のレーティング:
rb - 勝敗の結果:
result
- 対戦相手のレーティング:
-
2.2.2 勝敗の結果
resultに基づいて、イロレーティングにより、藤井8冠のレーティングraを更新
-
k = 16
# A's probability of winning calculated from the Iro rating
W_AB = 1.0/(10**((rb-ra)/400.0) + 1)
# case A wins
if result:
new_ra = ra + k * (1-W_AB)
else: # case B wins
new_ra = ra - k * W_AB
ra = new_ra
N対局終了後の藤井8冠のレーティングraを記録M個の記録されたレーティングのヒストグラムを作成- ヒストグラムをガウス分布でフィッティング
下の動画は、レーティングra=2118から開始して、
直近30対局の成績表からN=10対局をランダムに抽出し、
10対局を順に行って、藤井8冠のレーティング推移を算出してから、
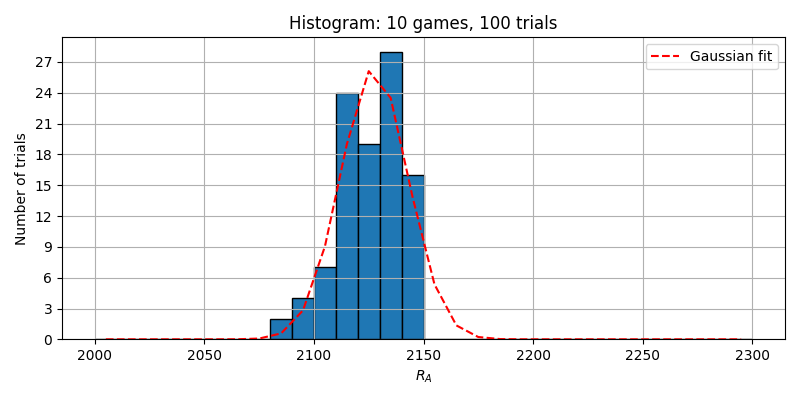
10対局目のレーティングをヒストグラムに追加していくことをM=100回行った様子を示しています。
この10対局をM=100回行った結果は、下図のようなヒストグラムとなり、直近30局の成績のいびつさがそのまま現れています。
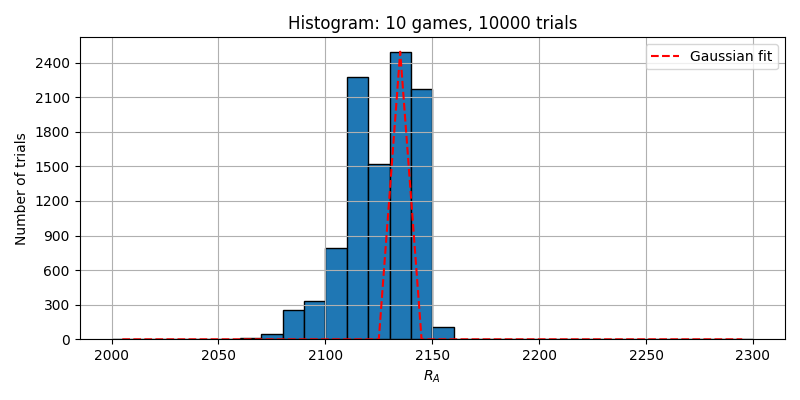
この10対局をM=10000回行っても、ヒストグラムのいびつさは無くなりませんでした。
これは、10対局が少なすぎるからのようです。 中心極限定理の観点からしても、対局数を増やしていく必要がありそうです。
試しに、100対局10000トライアル、1000対局10000トライアル、10000対局10000トライアルと増やしていくと、 ヒストグラムはガウス分布に近づき、フィッティングしたガウス分布の平均も2191くらいで変わらなくなっていきました。
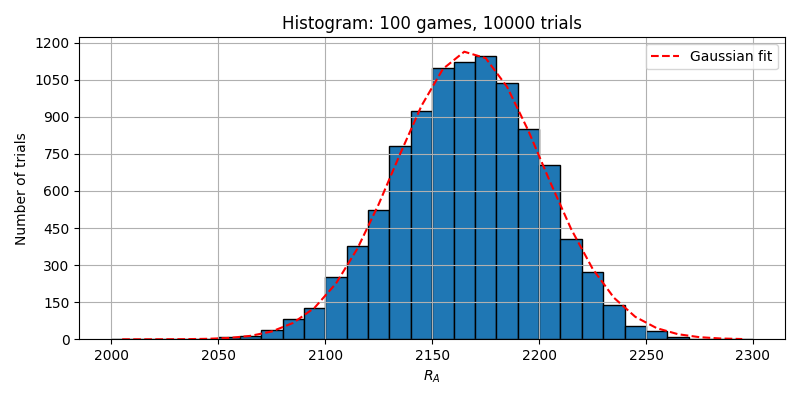 100対局を10000トライアルした場合のヒストグラム
100対局を10000トライアルした場合のヒストグラム
(ガウス分布の平均:2167.31093、標準偏差:34.3918987)
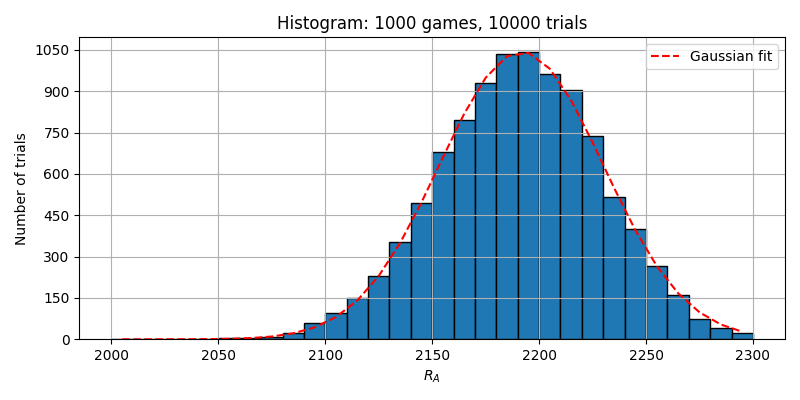 1000対局を10000トライアルした場合のヒストグラム
(ガウス分布の平均:2191.66157、標準偏差:38.3252676)
1000対局を10000トライアルした場合のヒストグラム
(ガウス分布の平均:2191.66157、標準偏差:38.3252676)
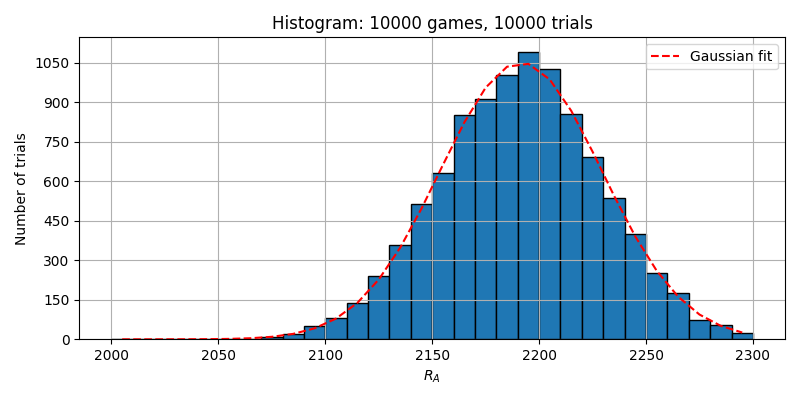 10000対局を10000トライアルした場合のヒストグラム
(ガウス分布の平均:2191.51815、標準偏差:38.0021477)
10000対局を10000トライアルした場合のヒストグラム
(ガウス分布の平均:2191.51815、標準偏差:38.0021477)
以上から、藤井8冠の棋士としてピークの満26歳におけるレーティングは、2191くらいだろうと推測されます。
藤井聡太8冠の出現確率の一推定
それでは、藤井聡太8冠の出現確率を推定します。
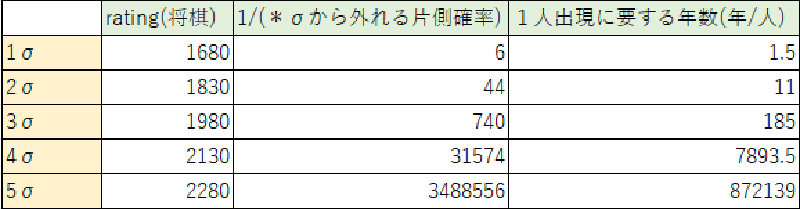
まず、将棋のレーティングにおける、標準偏差σと確率の関係は概ね下表のようになっています。(*はワイルドカード記号)
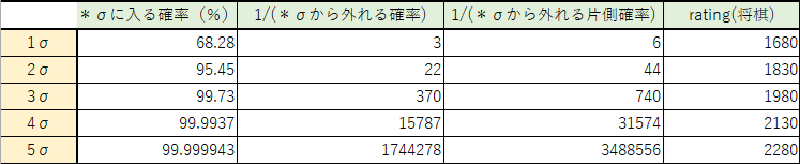
❗ 推定されたレーティングの2191は$4\sigma$の外にあります。
次に、毎年4名がプロ棋士になることから、1人出現年数は$n=1,…, 5$に対して
$$1人出現年数 = \frac{1}{4(人/年)\times n \sigmaから外れる片側確率}$$
と定義されます。
したがって、レーティングと1人出現年数の対応表は以下のようになります。
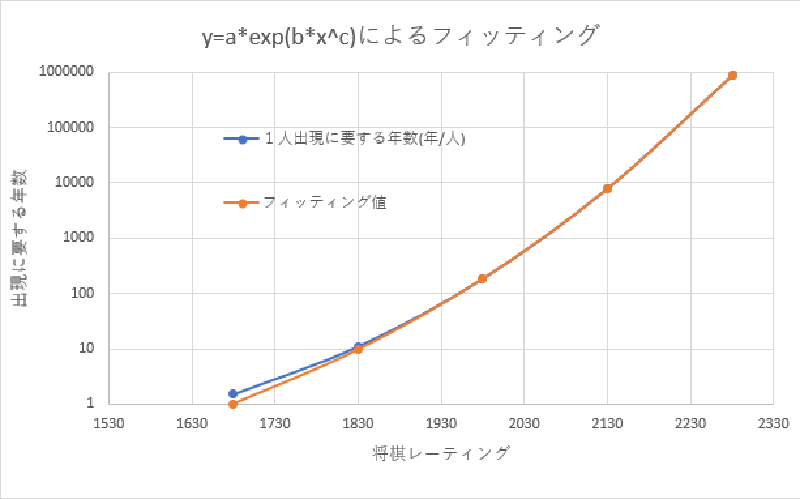
これをグラフにすると、テイラー展開(ベキ級数)ではフィッティングできないくらい急上昇するので、 急上昇する関数
$$ y = a \cdot e^{bx^c}$$
を用いて、$a, b, c$の値をフィッティングしますと、下図のようになりました。 ($a = 0.00547448, b = 1.378e-13, c = 4.21$)
それでは、このフィッティングした関数に、推定される藤井8冠のレーティングの2191を代入してみましょう。
結果は872,139年
となりました。 つまり、藤井聡太8冠の出現は、872,139年に1人というとんでもなく希有な事象であると推定されました。
おわりに
本記事では、藤井聡太8冠の出現確率を推定してみましたが、872,139年に1人という、とてつもなく稀な事象という結果になりました
次の藤井聡太は、次の類人猿が現れる前に現れるのでしょうか?