将棋棋士レーティング分布とガウス分布

はじめに

現在、将棋界は藤井聡太二冠、豊島将之竜王、渡辺明名人、永瀬拓矢王座の「4強の時代」と言われています。

本記事では、「4強の時代」は統計的にもそう言えるかどうかをガウス分布へのフィッティングを通して分析します。

将棋棋士レーティングの度数分布

まず、2021年3月28日現在の将棋棋士レーティングの分布を度数分布図にします。

下図がその度数分布図です。こうすると、視覚的に分りやすいでしょう。

確かに、右端の赤丸で囲んだ「4強」は突出した存在であることが窺われます。

ガウス分布でのフィッティング

では、この「4強」が突出した存在なのを判別するために、度数分布を次式のガウス分布で近似してみます。

$$ f(x; A, \mu, \sigma) = \frac{A}{\sigma \sqrt{2\pi}}e^{(x-\mu)^2/2\sigma^2} $$

ここで
　$A$: 振幅
　$\mu$: 中心
　$\sigma$: 標準偏差
を意味します。

ガウス分布による近似には、非線形最小二乗法を用いたモデルフィッティングを行うためのPythonライブラリである LMFITを使用する簡単です。

LMFITを使用したPythonスクリプトは以下のようになります。

import argparse
import numpy as np
import matplotlib.pyplot as plt

from lmfit import Minimizer, Parameters, report_fit
from lmfit.lineshapes import gaussian


def residual(pars, x, data):
    model = gaussian(x, pars['amp_g'], pars['cen_g'], pars['wid_g'])

    return model - data


def main():

    parser = argparse.ArgumentParser()

    parser.add_argument('--input', '-i', default='sample.csv')
    args = parser.parse_args()

    sample = np.loadtxt(args.input, delimiter=',')
    x = sample[:,0]
    data = sample[:,1]

    pfit = Parameters()
    pfit.add(name='amp_g', value=2000)
    pfit.add(name='cen_g', value=1500)
    pfit.add(name='wid_g', value=150)

    mini = Minimizer(residual, pfit, fcn_args=(x, data))
    out = mini.leastsq()
    best_fit = data + out.residual

    report_fit(out.params)

    plt.bar(x, data, edgecolor="black", width=20.0, linewidth=1)
    plt.plot(x, best_fit, 'r--', label='Gaussian fit')
    plt.legend(loc='best')
    xlabel='rating'
    ylabel='number of players'
    plt.xlabel(xlabel)
    plt.ylabel(ylabel)
    plt.savefig('out.png')
    plt.clf()


if __name__ == '__main__':
    main()

実行は、「-i」オプションを使用して、将棋棋士レーティングの度数分布のcsvファイルを入力データとして渡します。
freq_20210329.csv

python gaussian_fitting.py -i freq_20210329.csv

結果として、下記が出力されました。

[[Variables]]
    amp_g:  3498.32419 +/- 215.011179 (6.15%) (init = 2000)
    cen_g:  1551.18020 +/- 10.9584676 (0.71%) (init = 1500)
    wid_g:  155.233287 +/- 11.1322590 (7.17%) (init = 150)
[[Correlations]] (unreported correlations are < 0.100)
    C(amp_g, wid_g) =  0.587

これより、フィッティングされたガウス分布のパラメータの値が分かります。

　振幅($A$)： 3498.32419 　中心($\mu$)： 1551.18020 　標準偏差($\sigma$)： 155.233287

【注意】LMFITのMinimizerクラスは、デフォルトの最小化手法として、Levenberg-Marquardt法を使用しています。 Levenberg-Marquardt法は、パラメータの初期値によっては、局所解に収束してしまう可能性があるので、初期値の選び方には注意が必要です。
また、内部では、信頼領域法を使った反復計算をしているので、結果には信頼区間も表示されます。

将棋棋士レーティングの度数分布をガウス分布でフィッティングした結果は、下図の赤点線のようになりました。

分析

一般に、ガウス分布を用いて、突出しているかどうかを判定する際には

• $1\sigma$区間: $\mu \pm \sigma$
• $2\sigma$区間: $\mu \pm 2\sigma$
• $3\sigma$区間: $\mu \pm 3\sigma$

を計算し、$2\sigma$区間に収まるかどうかを見て、もし収まらなければ突出した存在と判断することがあります。

それでは、今回の結果は、どうでしょうか？

2021年3月28日現在の上位5人のレーティングは下表の通りです。

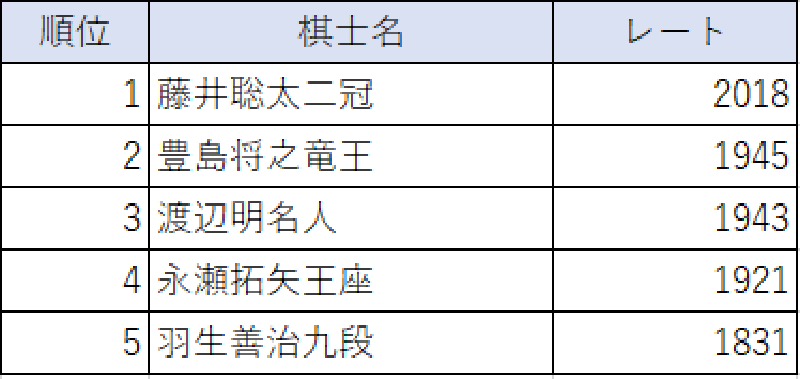
一方、

　$\mu + 2\sigma = 1861.646774$ 　$\mu + 3\sigma = 2016.880061$

ですので、見事に、$2\sigma$区間に収まらまらないのは、4強の藤井聡太二冠（2018）、豊島将之竜（1945）王、渡辺明名（1943）人、永瀬拓矢王座（1921）だけという結果になりました。

また、藤井聡太二冠だけが$3\sigma$区間に収まらず、その中でもさらに突出した存在であることを示しています。

最後に

将棋界は現在、藤井聡太二冠、豊島将之竜王、渡辺明名人、永瀬拓矢王座の「4強の時代」と呼ばれていますが、これは、統計的にも正しい表現であることが分かりました。

また、その中でも、藤井聡太二冠はずば抜けた存在であることが分かりました。

• lmfit