OpenFOAMを使った溶岩流の解析
By M.Sato
概要
今回は、OpenFOAMを使った溶岩流の解析例を紹介する。
📖 参考にした元の論文はここにある。
溶岩の流れは、温度を考慮して流動場と自由表面を計算する必要がある。
OpenFOAMには、等温場のニ相流を計算するためにinterFoamというソルバーが用意されているが、 温度場の計算は含まれていない。 ここでは、元論文の著者に習い、 interFoamを拡張し温度場の計算を追加したinterThermRadConvFoamというソルバーを作成した。
🔧 元論文の著者が作成したソルバーはv1912用であり、最新版のOpenFOAMでは動作しないため、 最新版(v2506)で動作するように修正を行った。
解析のモデル化について紹介を行った。 いくつかの解析を実施し、新しく作成したソルバーはv1912用のソルバーと同等の計算ができることを確認した。
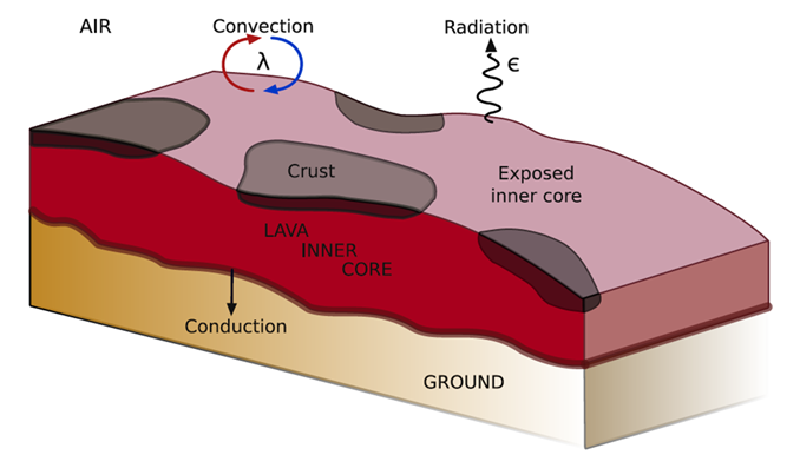
図:溶岩流の解析モデル概念図(元論文のFig.3より引用)
基礎方程式
解析に使用している基礎方程式を示す。
$$ \begin{align} \frac{\partial \alpha}{\partial t} + \nabla \cdot (\mathbf{u} \alpha) &= 0 \\ \nabla \cdot \mathbf{u} &= 0 \\ \frac{\partial \rho \mathbf{u}}{\partial t} + \nabla \cdot (\rho \mathbf{u} \mathbf{u}^T) &= -\nabla p + \nabla\cdot \mathbf{\tau} + \rho \mathbf{g} + \mathbf{f}_\Sigma \\ \frac{\partial \rho c_p T}{\partial t} + \nabla \cdot (\rho c_p T \mathbf{u} ) - \chi_\Sigma \nabla^2 (kT) &= -\frac{\epsilon \sigma_{SB} f A_{fs}}{V} (T^4 - T_{env}^4)-\frac{h f A_{fs}}{V} (T - T_{env}) \end{align} $$
ここで、
- $\alpha$:溶岩の体積分率
- $\mathbf{u}$:速度ベクトル
- $t$:時間
- $\rho$:密度
- $p$:圧力、
- $\mathbf{\tau}=\mu\left[\nabla\mathbf{u}+(\nabla\mathbf{u})^T\right]$:粘性応力テンソル
- $\mathbf{g}$:重力加速度ベクトル
である。 $\mathbf{f}_\Sigma$は表面張力に起因する体積力であり、以下の式で表される。
$$ \mathbf{f}_\Sigma = \sigma_\Sigma \kappa_\Sigma \nabla \alpha,\quad \kappa_\Sigma = - \nabla \cdot \left( \frac{\nabla \alpha}{|\nabla \alpha|} \right) $$
- $\kappa_\Sigma$:界面の曲率
- $\sigma_\Sigma$:表面張力係数
を表す。なお以下の解析では表面張力の効果は無視している。
- $c_p$:比熱
- $T$:温度
- $k$:熱伝導率
- $\epsilon$:放射率、$\sigma_{SB}$はステファン・ボルツマン定数
である。
- $f$:界面においてlava-inner-coreが露出している割合を表すための変数であり以下の解析では1.0と仮定している。\
- $T_{env}$:周囲温度
- $h$:対流熱伝達率
- $\chi_\Sigma$:界面位置を示す指示関数であり、界面での熱拡散を抑制するために使われる。 その値は、界面上のセルでゼロ、それ以外のセルで1の値を持つ関数である。
VOF法を使って計算することになるため、流体の物性値は各相の体積分率に基づいて以下のように計算される。
$$ \begin{align} \rho &= \alpha \rho_{lava} + (1-\alpha) \rho_{air} \notag \\ \mu &= \alpha \mu_{lava} + (1-\alpha) \mu_{air} \notag \\ \rho{c_p} &= \alpha \rho_{lava}{c_{p,lava}} + (1-\alpha) \rho_{air}{c_{p,air}} \notag \\ k &= \alpha k_{lava} + (1-\alpha) k_{air} \notag \end{align} $$
粘度式
溶岩の粘度には非アレニウス型のVogel-Fulcher-Tammann (VFT)式を用いている。これは以下の式で表される。
$$ \begin{align} log(\mu) &= A + \frac{B}{T - C} \notag \end{align} $$
ここで、$\mu$は粘度[Pa.s]、$T$は絶対温度[K]である。 $A,B,C$は溶岩の組成に依存しており実験データに基づいて決定される定数である。
溶岩表面からの熱移動のモデル化
溶岩流が空気と接する部分では、溶岩表面から空気中に熱が放出される。
この熱放出の原因は、熱輻射による効果と対流熱伝達による効果がある。
また溶岩流が地面と接触する部分では、地面に熱が移動することになる。
もし溶岩流表面が解析領域の境界になっている場合、直接熱フラックス境界条件を指定できるが、 今回の計算モデルではVOF法を使っているため、溶岩表面は解析領域内部に含まれことになる。
そのため、溶岩流が空気と接している部分では、流体のエネルギー保存式に等価な熱ソース項として指定した。
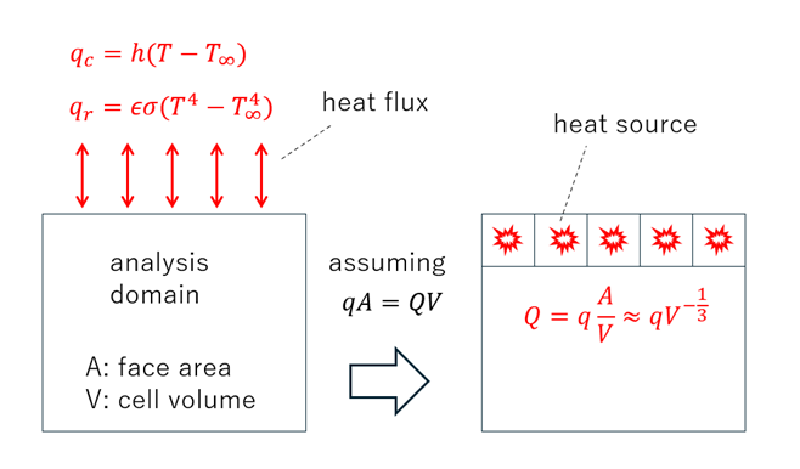
図:溶岩表面からの熱移動モデル
地面からの熱フラックス
地面からの熱移動を考慮するために熱伝達境界を設定した。
元論文では、下図に示すように地面境界に対してexprMixedタイプの境界条件を使用しているが、 境界条件の表現式が正しくないと思われるため、ここではcodedMixedタイプの境界条件に書き直して使用した。
⚠️ 元論文の問題点:
- 熱伝導率をPr数から逆算する式になっているが粘度が含まれていない
- 流体の相分率を考慮した熱伝導率になっていない
- mag(pos())は原点からの距離であり壁面からの距離ではない

図:元論文で使用されているexprMixed境界条件
mixedタイプの境界条件の設定方法を説明した図を以下に示す。
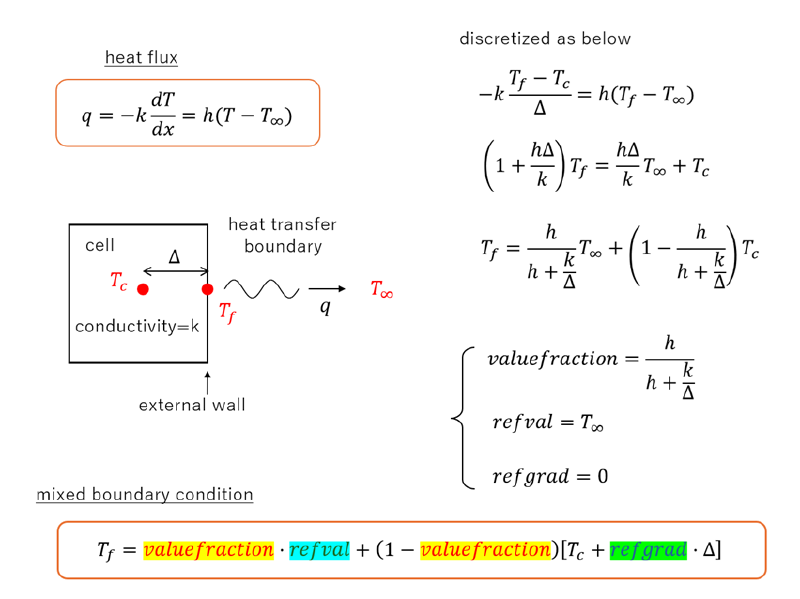
図:mixedタイプ境界条件の設定方法
対流熱伝達効果の考慮
溶岩表面(空気との界面)からの対流熱フラックスは次式で表される。
$$ q_{conv} = h (T - T_{env}) $$
ここで、
- $q_{conv}$:単位面積あたりの対流熱フラックス
- $h$:対流熱伝達率
- $T$:溶岩の表面温度
- $T_{env}$:周囲環境の温度
を表す。熱フラックスにface面積をかけてセル体積で割ることにより、 溶岩自由表面セルに対する等価な発熱項を得ることができる。
この発熱項を線形近似してエネルギー保存式に組み込む。
$$ \begin{align} Q_{conv} &= \frac{ h f A_{fs} }{V} (T - T_{env}) \notag \end{align} $$
この発熱項は線形式となっており、そのままエネルギー保存式に組み込むことができる。
熱輻射効果の考慮
溶岩表面(空気との界面)からの輻射熱フラックスは次式で表される。
$$ \begin{align} q_{rad} = \epsilon \sigma_{SB} (T^4 - T_{env}^4) \notag \end{align} $$ ここで、
- $q_{rad}$:単位面積あたりの放射熱フラックス
- $\epsilon$:溶岩の放射率
- $\sigma_{SB}$:ステファン・ボルツマン定数
- $T$:溶岩の表面温度
- $T_{env}$:周囲環境の温度
を表す。熱フラックスにface面積をかけてセル体積で割ることにより、 溶岩自由表面セルに対する等価な発熱項を得ることができる。
この発熱項を線形近似してエネルギー保存式に組み込む。
$$ \begin{align} Q_{rad} &= \frac{ \epsilon \sigma_{SB}f A_{fs} }{V} \left( T^4 - T_{env}^4 \right) \notag \\ &=\beta (T_{env}^4 + 3 T^4)-4 \beta T^3 T \notag \end{align} $$
ここで $\beta=\frac{\epsilon\sigma_{SB}f A_{fs}}{V}$である。
解析手法
溶岩流を解析するためには、2流体(溶岩と空気)の界面を追跡する必要がある。 高温の溶岩は流出後は周囲温度によって冷却される。
溶岩の粘度は温度に依存するため、温度場の計算も必要になる。
ここでは、元論文の著者に習い、二流体の等温場の解析追跡ソルバー interFoamを拡張し、 温度場の計算を追加したinterThermFoamというソルバーを作成した。
なお、標準版のOpenFOAMには、compressibleInterFoamというソルバーがあり、 圧縮性流体として同等の解析を行うことができると考えられるが、 今回作成したソルバーは二相の流体をそれぞれ非圧縮性流体として扱っている点が異なる。
ソースプログラムの修正
元論文の著者はOpenFOAM v1912を使っているが、現在のOpenFOAMの最新版で動作するようにソースプログラムを修正した。
主な修正点は以下の通りである。
-
熱伝達境界の実装: 前述のように地面と接触する部分では、熱伝達境界を設定する。 前述のように元論文では、OpenFOAMのexprMixedタイプの境界条件を使っているが、正しく実装されていないと思われる。 ここではcodedMixed境界条件に変更し、正しく熱伝達境界条件を実装した。
-
流体の熱伝導率を入力: 元論文では、流体の熱伝導率をPr数から逆算しているが、粘度が温度関数となっているため熱伝導率は粘度に比例するような表現式になる。 実際には溶岩の粘度と熱伝導率は独立のパラメータとして指定すべきであるため、 ここでは流体の熱伝導率を直接入力するように修正した。
解析例
軸対称モデルを使った解析
これは元論文ではBM3として言及されているものである。 シリコンオイルを使った実験データと比較している検証ケースである。
📝 解析条件:
- 粘度は定数として扱っているため、流れ場と温度場は非連成
- 元論文と同じ条件で計算を実施
- 動的メッシュ精細化は使用していない(クラッシュするため)
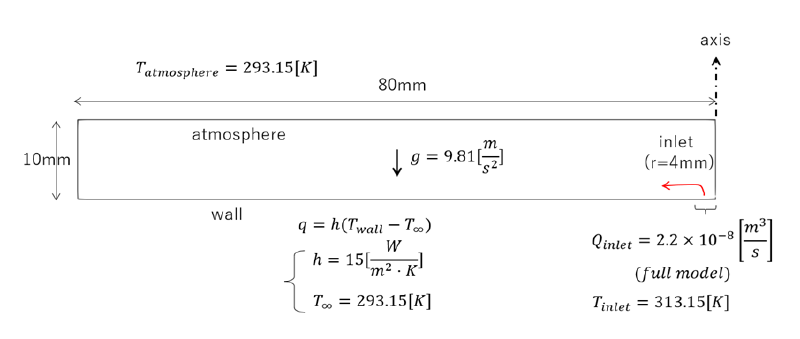
図:軸対称モデルの解析対象
解析は頂角5度の扇型領域を作成し、軸対称モデルとして計算を行った。
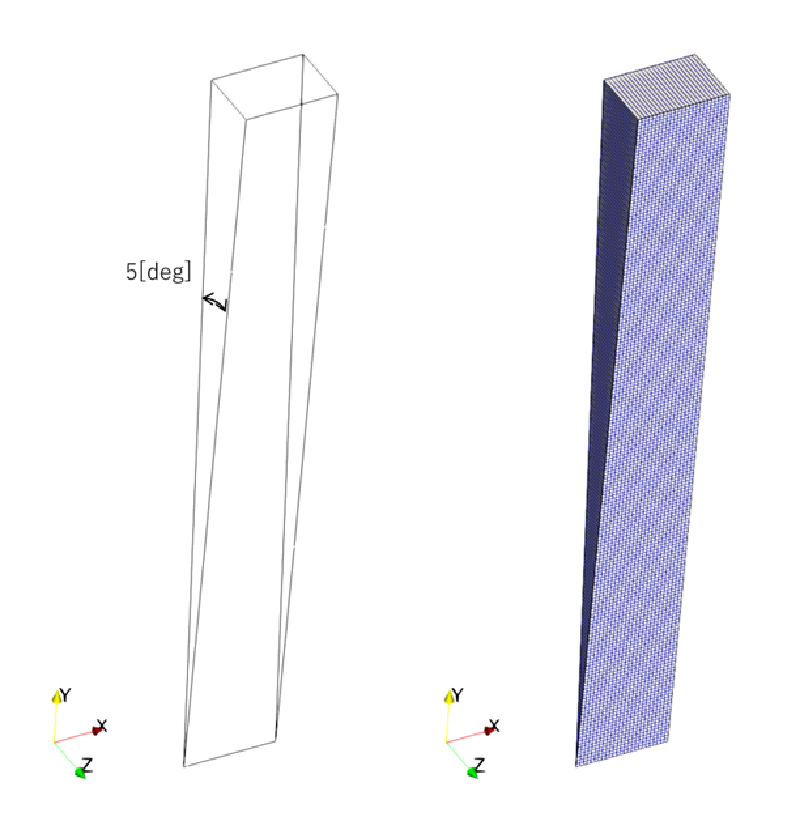
図:解析領域とメッシュ
計算に使用した物性値を以下に示す。
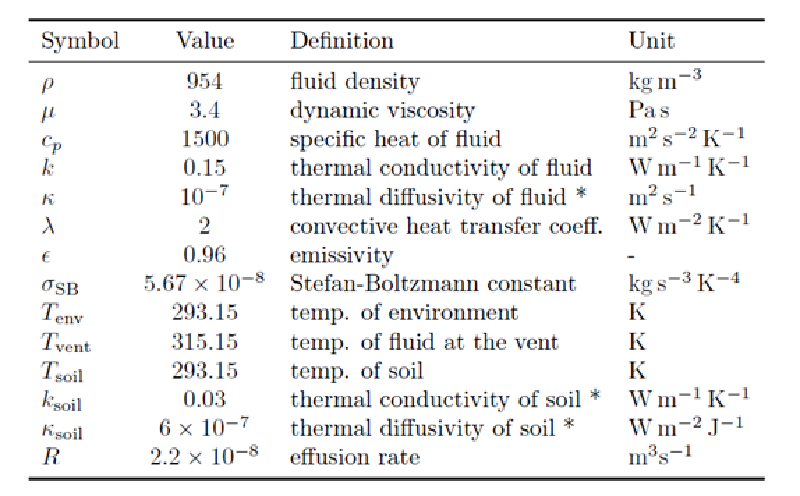
表:物性値一覧
計算結果
計算結果のアニメーションを以下に示す。コンター図は温度を表示している。液相の広がりは 元論文中の結果と類似したものになっていることがわかる。
動画:温度分布のアニメーション
斜面モデルを使った解析
傾斜角30度の斜面を溶岩が流れ落ちる様子を計算したものである。
📝 解析条件:
- 斜面には直径0.1mの円形開口部があり、ここから溶岩が流出
- 溶岩の流出流量:$10^{-5}[m^3/s]$
- 溶岩の温度:$1350[K]$
- 解析時間:1000[sec]まで
- 動的メッシュ精細化は使用していない(クラッシュするため)
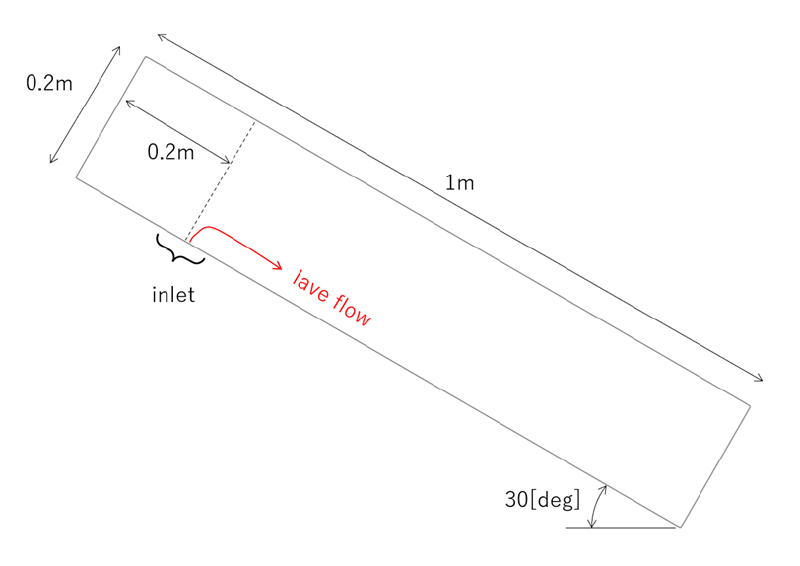
図:解析対象領域
計算に使用した物性値を以下に示す。
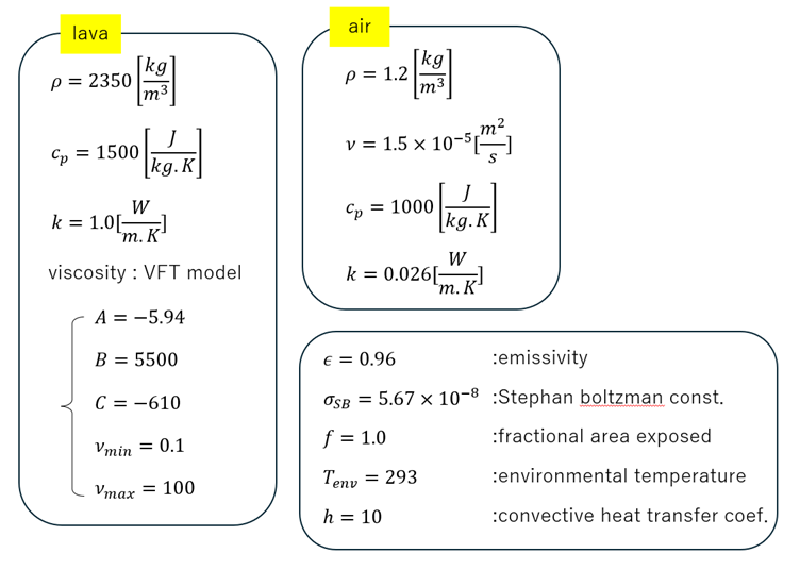
表:物性値一覧
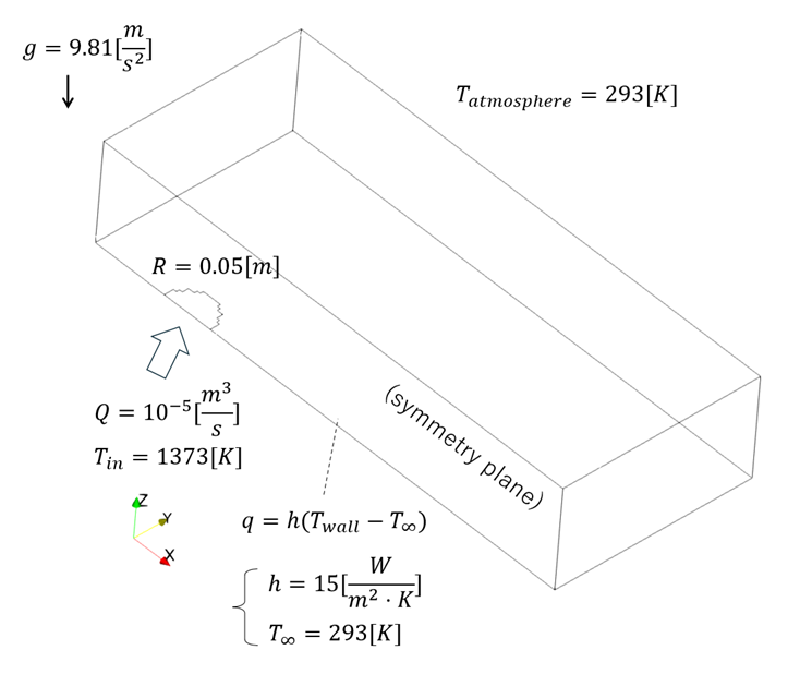
図:解析モデル
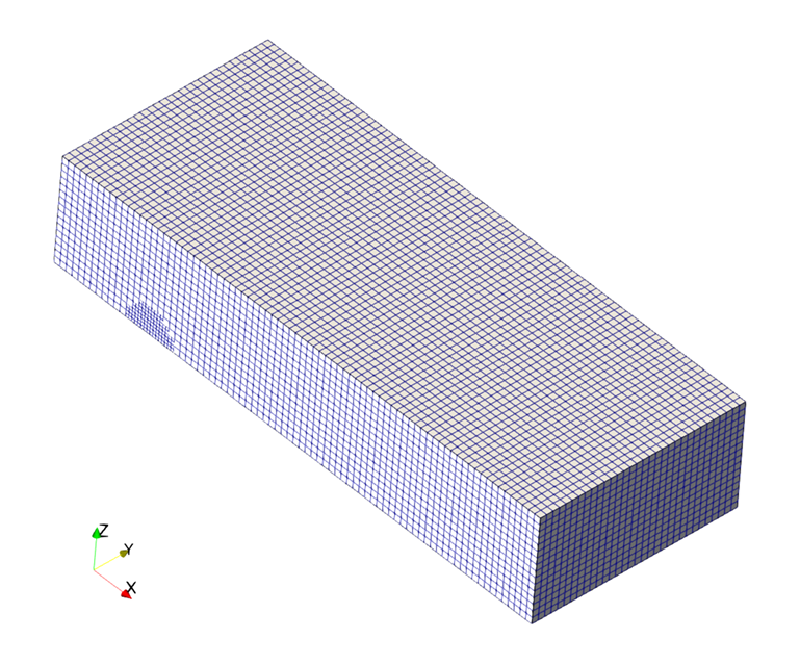
図:メッシュ分割
計算結果
以下に計算結果を示す。
動画:界面上の流速ベクトル図
動画:界面上の温度コンター図
動画:動粘度コンター図
動画:界面形状を表すセル位置
界面形状を表すセル位置はVOF関数($\alpha$)の値が0.01から0.99の範囲に相当するセルを抽出して表示したものである。
- $\alpha<0.01$:空気相
- $\alpha>0.99$:溶岩相
これは OpenFOAMの組み込み関数nearInterface()を使って得られたものである。
⚠️ 本来、界面として抽出されたセルは空気-溶岩間に一個だけのはずであるが、 実際には複数層のセルが抽出されていることがわかる。
考察
今回の解析で確認された問題点を以下にまとめる。
❌ 動的メッシュ精細化との相性問題
地面に熱伝達境界(codedMixed)を設定した上で動的メッシュ精細化を有効にすると、 計算がクラッシュする現象が発生した。
なお、試しにオリジナルのv1912で作成された interThermRadConvFoamソルバーでcodedMixed境界を使っても同様の現象が発生している。
この現象の原因は明確ではないが、 熱伝達境界条件と動的メッシュ精細化の組み合わせに問題がある可能性がある。
❌ 界面セルの抽出問題
斜面モデルで示したように界面形状を表すセルが溶岩-空気界面上の一個のセルでなく、 界面をまたがる複数のセルとして抽出されている箇所がある。
今回の計算モデルでは熱フラックスを溶岩表面上のセルに対する熱ソース項として指定しているため、 このような現象が発生すると熱ソース項が過大に設定されることになる。
❌ 地面隣接セルの誤認識
地面に隣接したセルも界面形状を表すセル位置として抽出されている。 ここは地面との間で熱伝達により熱が移動する境界であるため、 空気側と接している界面と認識されると過剰な熱ソース項が発生することになる。
💡 今回紹介した計算モデルは興味深いものであるが、 精度のよい計算を行うためには界面の扱いをもっと正確に扱う必要があると思われる。
まとめ
✅ 溶岩の流動をOpenFOAMを使って解析する手法を紹介した。
✅ 元論文の著者が作成したソルバーを**最新版のOpenFOAM(v2506)**で動作するように修正し、いくつかの解析例を示した。
✅ 今回のソルバーについていくつかの問題点を指摘した。
✉ 参考: 今回の解析で使用したOpenFOAMのソースコード(v2506用)および解析データをご希望の方は、お問い合わせフォームよりご連絡ください。
弊社の解析事例
弊社の流体解析事例については、下記のリンクからご覧ください.