入れ子になったスライディングメッシュ
By M.Sato
概要
Ansys Fluentでは入れ子になったスライディングメッシュを扱うことが可能である。
ここでは簡単な二次元モデルを使い、検証計算を行ってみた。以下に解析の手順を示す。 なお流体の混合の様子を可視化するためにユーザ定義変数(UDS)を同時に計算するようにした。
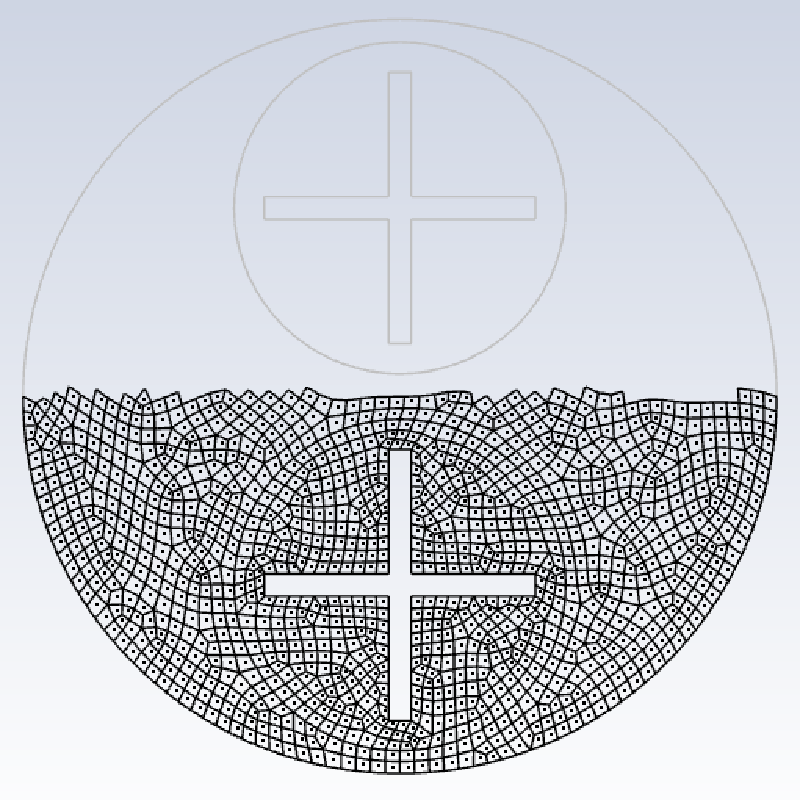
解析モデル
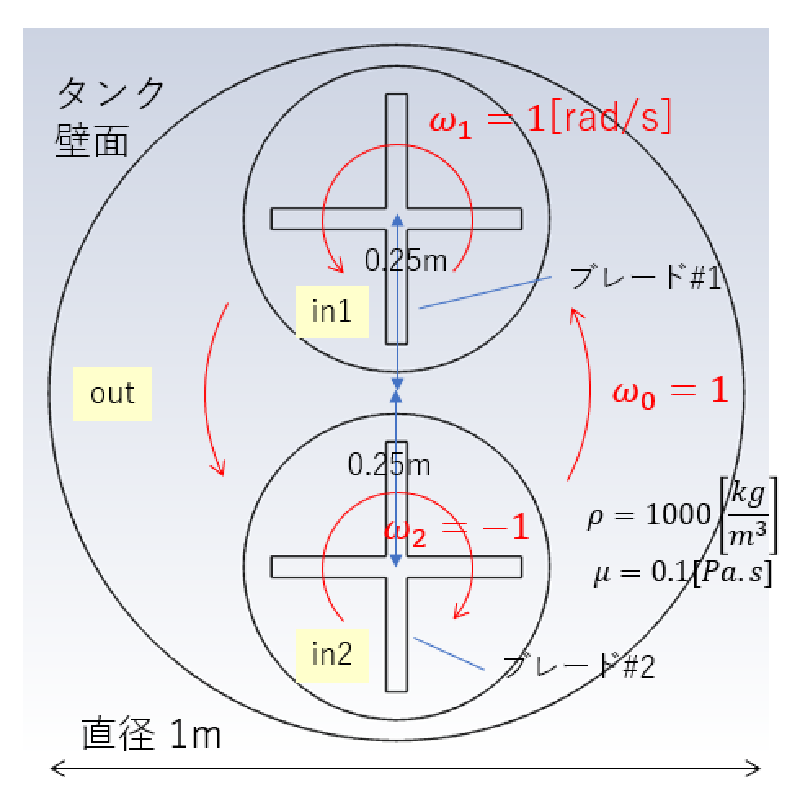
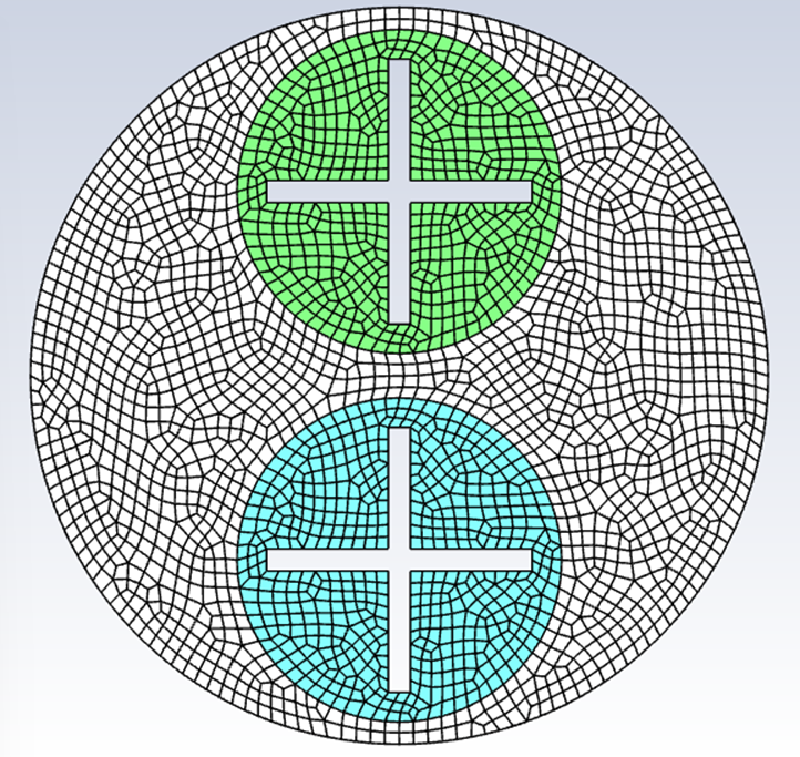
解析モデルを示す。
４枚羽の回転ブレード（パドル翼）が二組あり、それらが回転する支持機構の上に設置されているような構造となっている。 従って、３種類の回転速度が必要である。 回転方向および回転角速度[rad/sec]は図に示す通りである。 $\omega_2$のみが逆方向に回転している。解析領域は"in1"、“in2”、“out"の三個のゾーンで構成されている。
モデル
今回の計算では流体に色をつけてその分布を追跡した。 解析領域の下半分に赤色マーカ（UDS=1)を設定するようにした。 UDS変数は移流により移動すると仮定した。
UDS変数の輸送方程式は以下である。
$$ \rho \frac{D S}{D t} = \rho \left(\frac{\partial S}{\partial t} + u_j\frac{\partial S}{\partial x_j} \right)= 0 $$
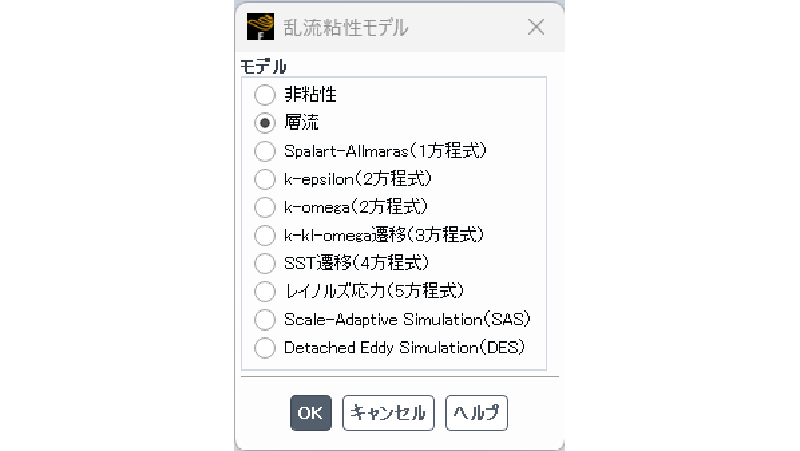
粘度モデル
流れ場は層流であるとした。
粘度モデル
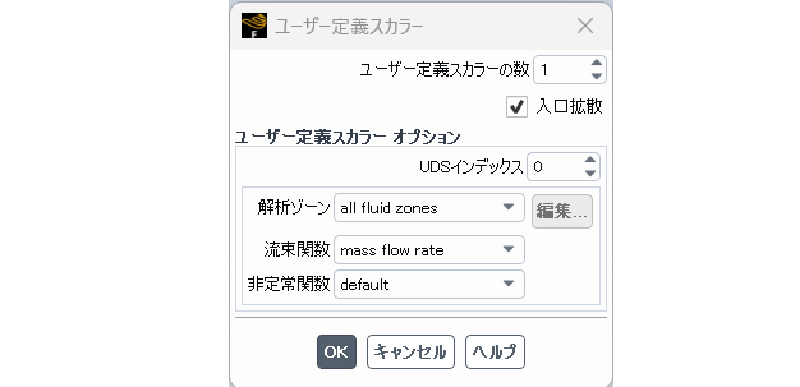
ユーザ定義変数
流れ場の計算に伴ってUDS変数も計算する。
UDS変数は流れの影響を受けるが、UDSから流れに影響を及ぼすことはない（すなわちパッシブスカラーとして扱う）。
uds指定
uds指定2
メッシュ分割
今回の解析ではスライディングメッシュモデルを使い、回転の効果を表現する。
従って３個の連続体ゾーンメッシュを独立に作成し、fluentの中で不連続インターフェイスを定義している。
メッシュ分割
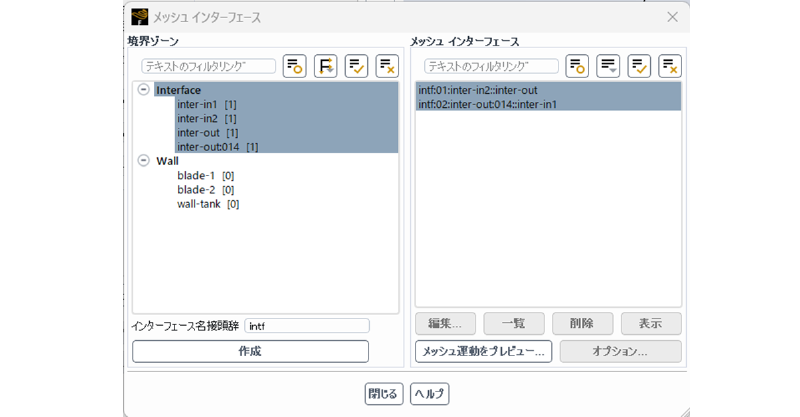
メッシュインターフェイスは２箇所ある（in1-out間およびin2-out間）。
これらはGUI上で interface境界ゾーンを選択して作成ボタンを押せば自動的に作成される。
インターフェイス
物性値
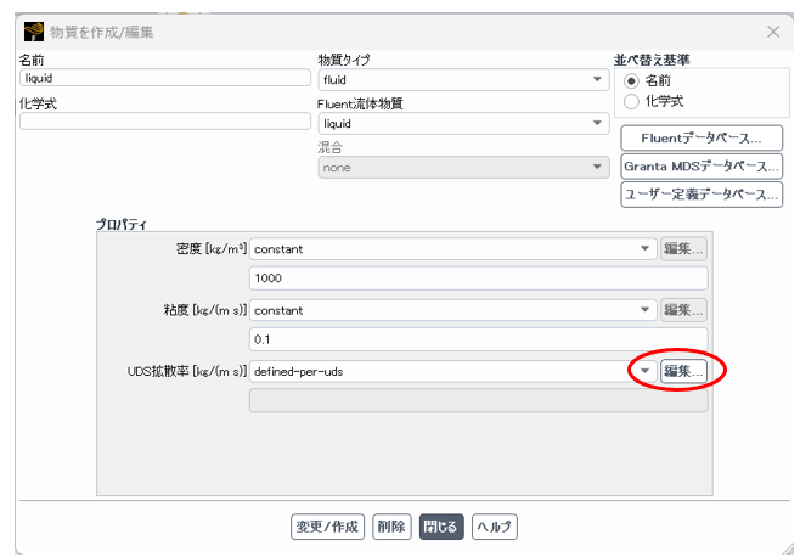
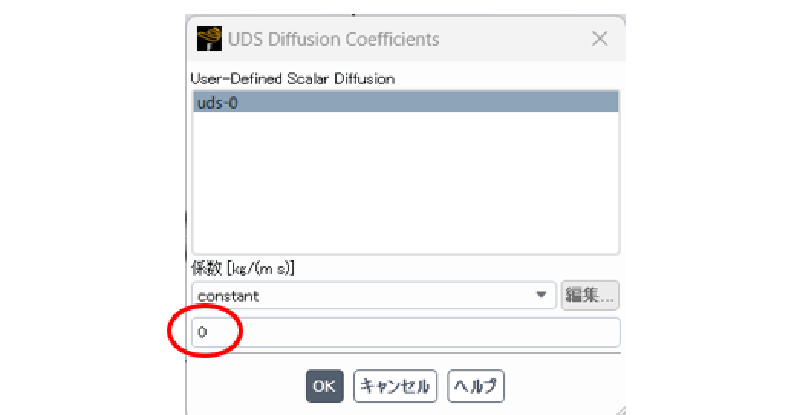
ここでは以下に示す物性値を仮定した。 なおUDS変数は移流効果のみにより移動することから拡散係数をゼロとした。
物性値1
物性値2
セルゾーン条件
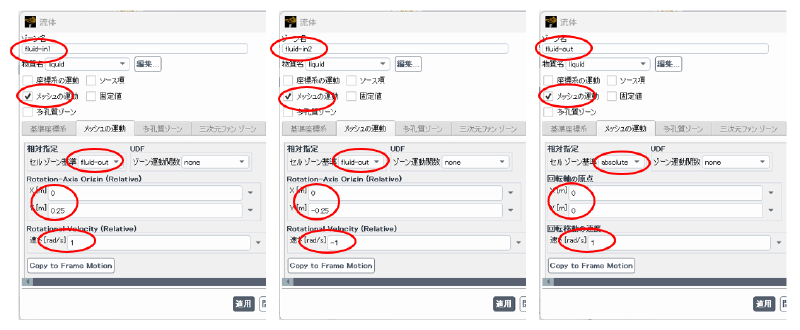
今回の計算ではゾーンin1, in2, out の全てが回転移動することになる。
セルゾーンに対する回転の設定は、以下の２種類の方法がある。
- 絶対座標に基づき、各ゾーンの回転中心、回転角速度を指定
- 親ゾーンからの相対座標に基づき、子ゾーンの回転中心、回転角速度を指定
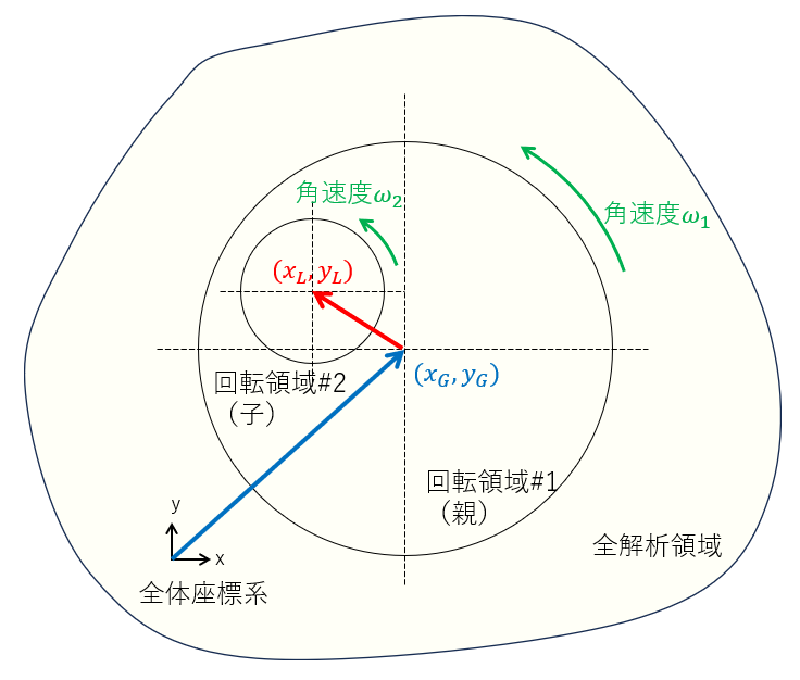
今回の計算では、ゾーン “out"については1.の方法、ゾーン"in1”、“in2"については2.の方法で設定を行った。 なお、絶対座標と相対座標の考え方を以下の図に模式的に示す。
相対座標を使う場合は、子ゾーンの回転中心は親ゾーンの回転中心からの相対座標になる。
また子ゾーンの回転速度は親ゾーンに対する相対的な値であることに注意する必要がある。
従って、子ゾーンの回転速度は基準とする座標系に依存して異なる。
$$ \omega_{(child-absolute)}=\omega_{(child-relative)}+\omega_{(parent)} $$
回転座標説明
セルゾーン
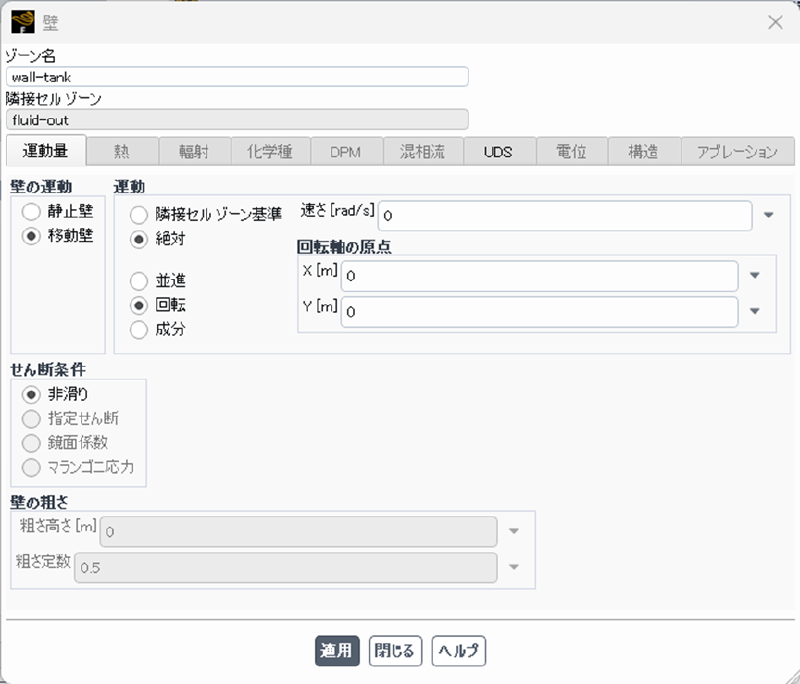
境界条件
タンク壁面（外周）は速度ゼロと指定した。
境界条件
局所座標系の定義
今回の計算は非定常解析であり、流体が静止している状態から始めて、最終的に”定常的な状態”に漸近すると考えられる。
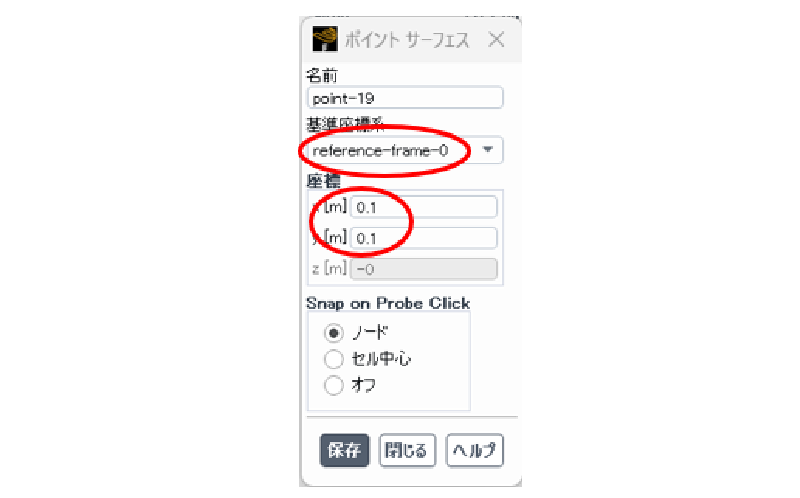
ここでは、回転ブレードの中心点から相対的に (0.1m, 0.1m)の位置に検査点を設置し、そこでのUDS変数の経時変化を調べるようにした。
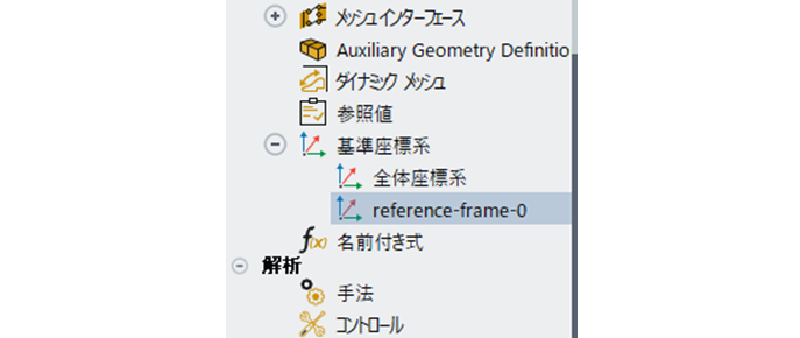
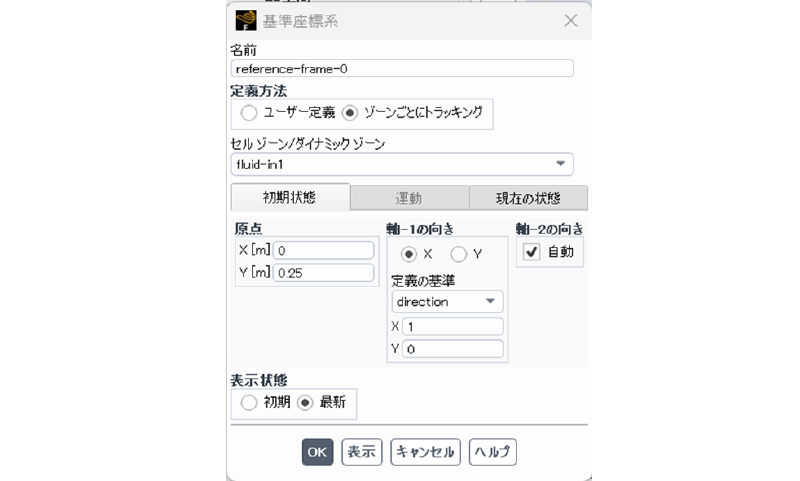
そのため、まず、局所座標を作成する。
局所座標
局所座標2
局所座標は図表示することで確認することができる。 以下に初期時刻とt=1[sec]後の座標系（および検査点）の位置を示す。
![局所座標(時刻 t=0[sec])](https://www.rccm.co.jp/icem/rccm_fluid/posts/nested_twin_blade/images/probe1.png)
局所座標(時刻 t=0[sec])
![局所座標(時刻 t=1[sec] : $\pi$ラジアン=57.3度回転している)](https://www.rccm.co.jp/icem/rccm_fluid/posts/nested_twin_blade/images/probe2.png)
局所座標(時刻 t=1[sec] : $\pi$ラジアン=57.3度回転している)
検査点の定義
検査点(point-19)は局所座標に基づき指定する。
検査点
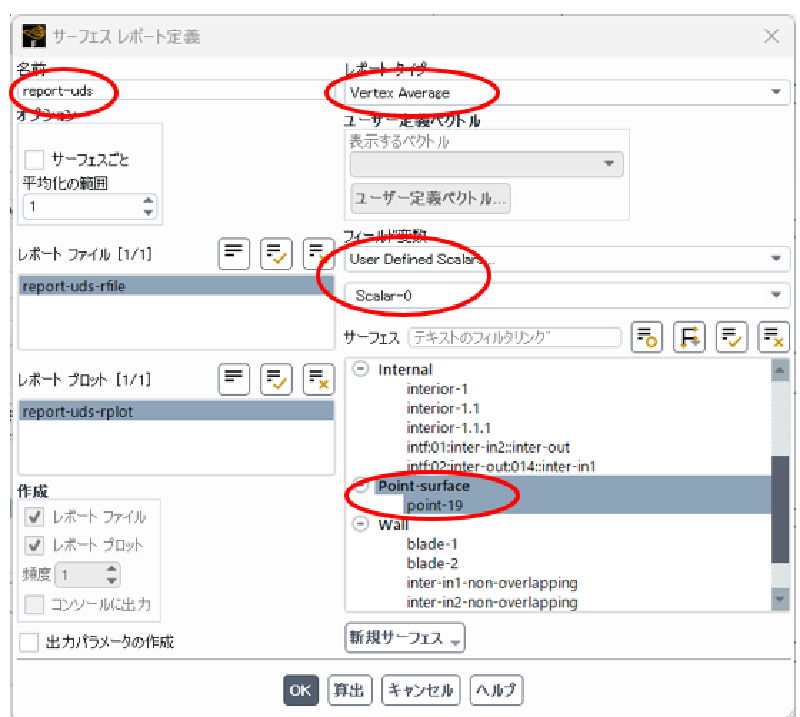
レポートの定義
上で作成した検査点でのUDS変数をモニターしておく。以下のように設定する。
レポート
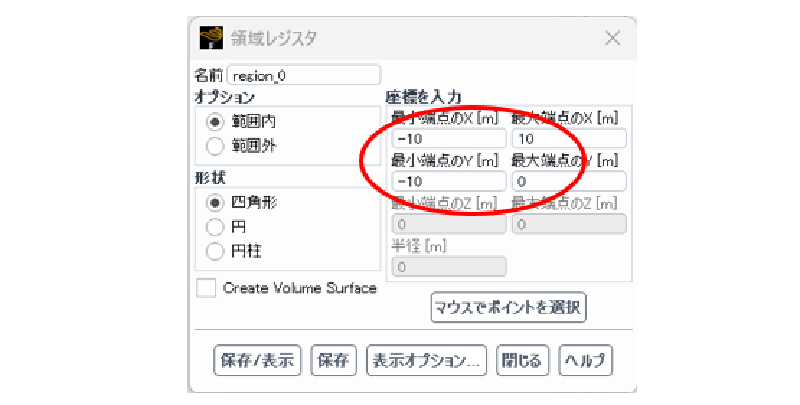
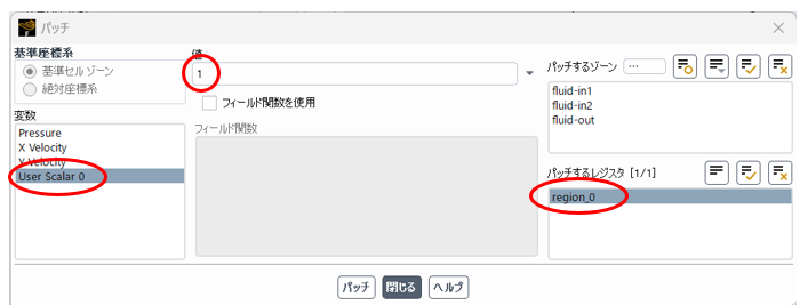
UDS設定ゾーンの作成
解析領域の下半分においてUDS=1と設定する。 まず、ゾーンレジスタを作成する。
レジスタ
レジスタ2
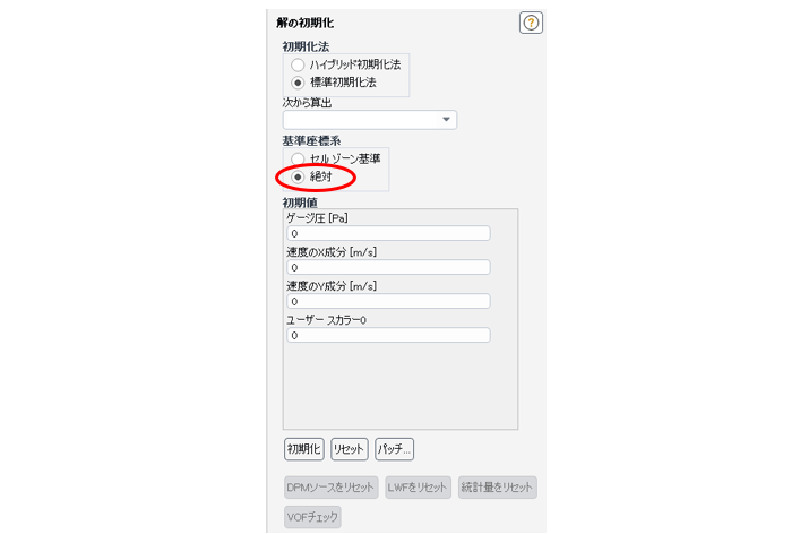
初期化
初期時刻において流速がゼロと指定する（絶対座標系基準）。また、パッチを使いUDS変数を指定する。
初期化
初期化2
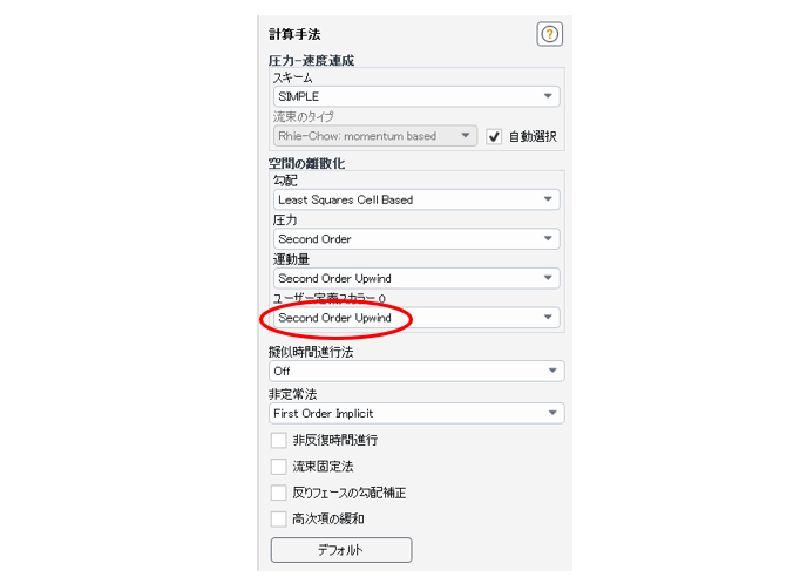
計算手法
UDSの移流項は二次精度風上法で離散化する。
計算手法
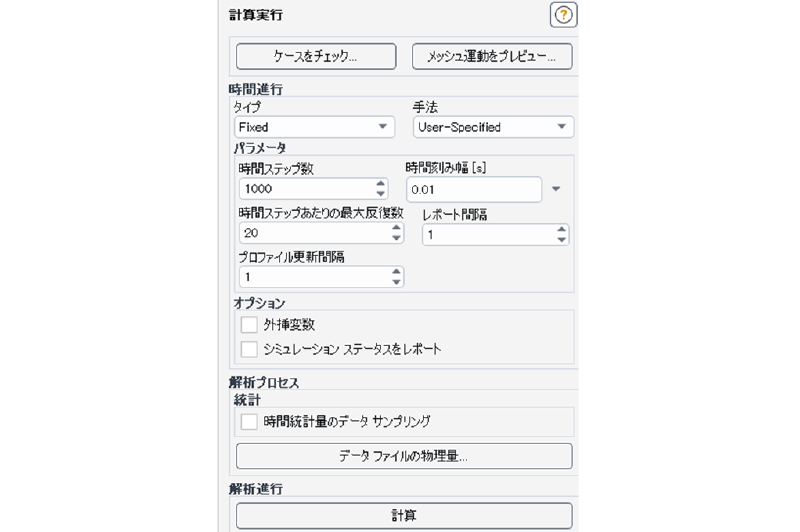
計算実行
時間刻み幅を 0.01 [sec]で1000ステップの実行を行った。
実行
計算結果
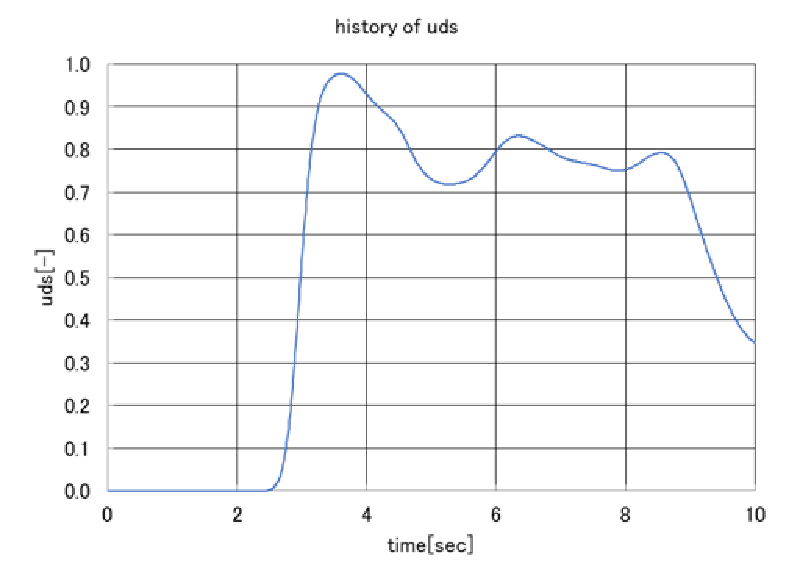
検査点におけるUDS変数の時刻歴図は以下のようになっている。 最終的なUDSの平均値は 0.5 であることから、まだ定常的にはなっていないことがわかる。
時刻歴
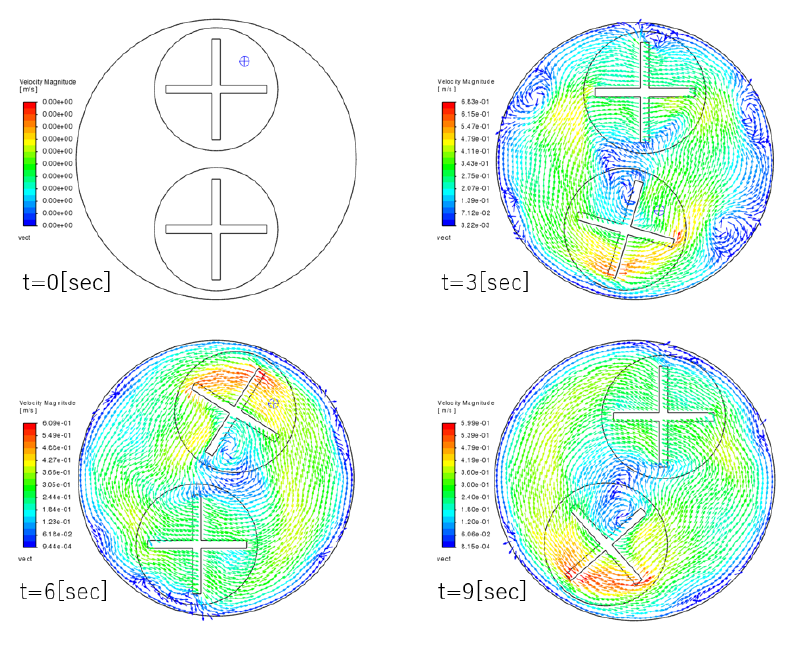
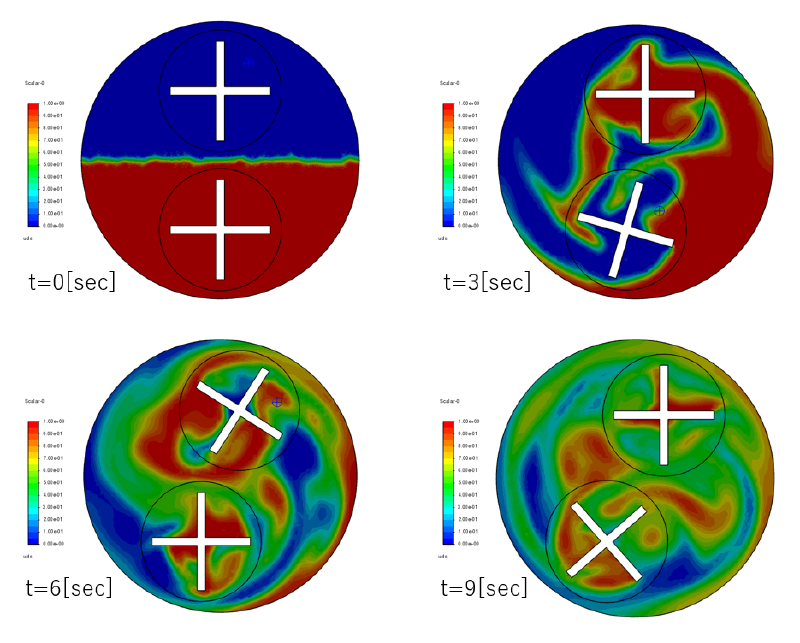
時刻t=0,3,6,9[sec]における流速ベクトルおよびUDSコンターは以下のようになっている。
図中の"in2"のブレード方向が常にx,y軸に平行になっているが、 これは全体座標系での回転角速度が $$\omega_{2,absolute}=\omega_{2,relative} + \omega_0= -1+1=0[rad/s]$$
となるためである。
同様に全体座標系でみた"in1"の回転角速度は実際には
$$\omega_{1,absolute}=1+1=2[rad/s]$$
である。
流速ベクトル
UDSコンター
cfd-postを使ったアニメーション作成
今回の解析結果を使い、cfd-post でアニメーションを作成することができる。
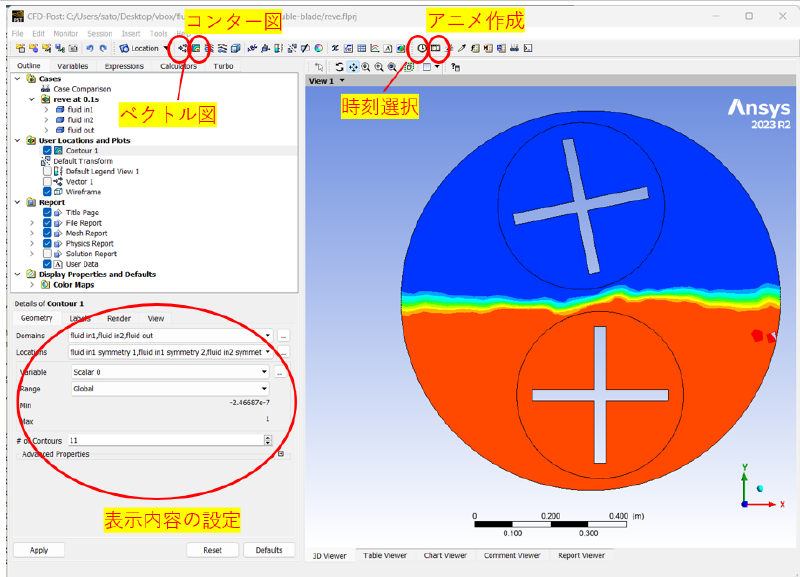
cfd-postの起動画面を示す。
fluentの解析実行時に作成されるflprjファイルをcfd-postで読み込むことで、fluentの計算結果をポスト処理で図表示することが可能である。 アニメーションは以下に示す数個のボタンを適当に押せば簡単に作成可能である。
cfdpost
cfdpostで作成したアニメーションは以下のようになった。
メッシュ
流速ベクトル
流速強度コンター
圧力コンター
UDSコンター
まとめ
fluentを使い、入れ子になった回転メッシュの計算を行ってみた。 解析の参考になれば幸いである。
弊社の解析事例
弊社の流体解析事例については、下記のリンクからご覧ください．