オーバーセット法の例

By M.Sato

January 8, 2024

概要

前報において入れ子になったスライディングメッシュを使った解析事例を紹介した。回転するメッシュの境界は回転対称な形状である必要があり、解析対象によっては適用できない場合もある。例えば、インペラーの回転半径が大きく隣接するインペラーと相互に干渉するような場合には使えない。

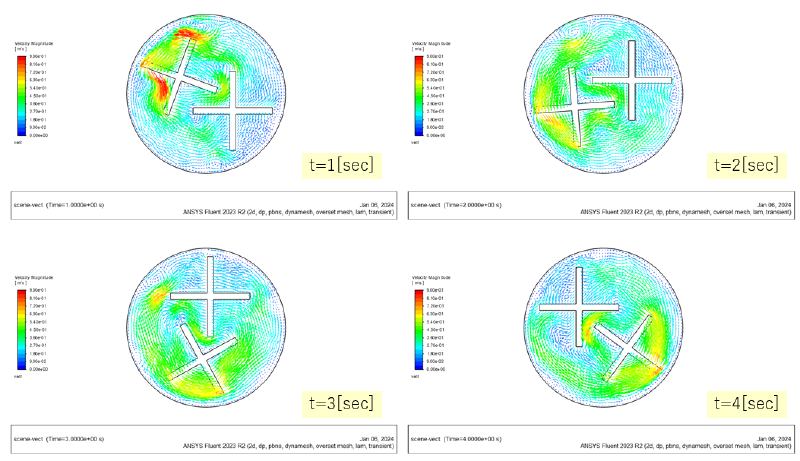
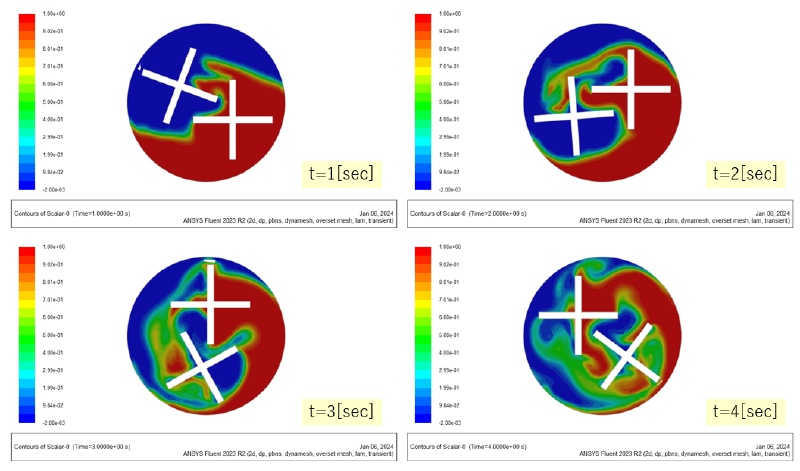
今回は、このような相互干渉するインペラー形状に対しても適用可能なオーバーセット法を紹介する。解析の例題は前報において使用したものと類似のものであり、インペラーのブレード長さが大きくなったものになっている。なお流体の混合の様子を可視化するためにユーザ定義変数(UDS)を同時に計算するようにした。

解析モデル

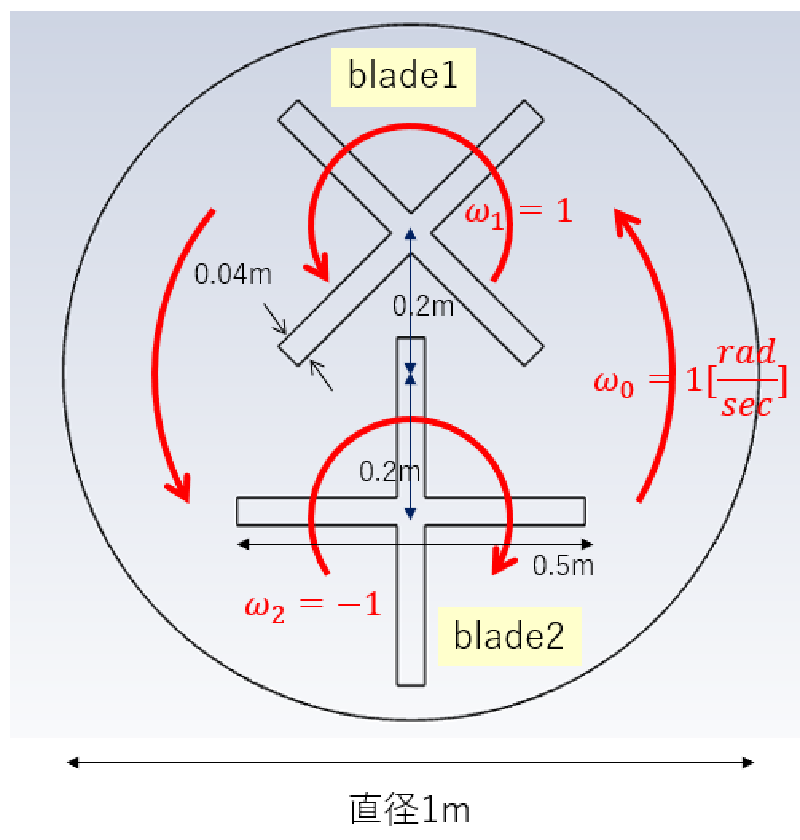
解析モデルを示す。

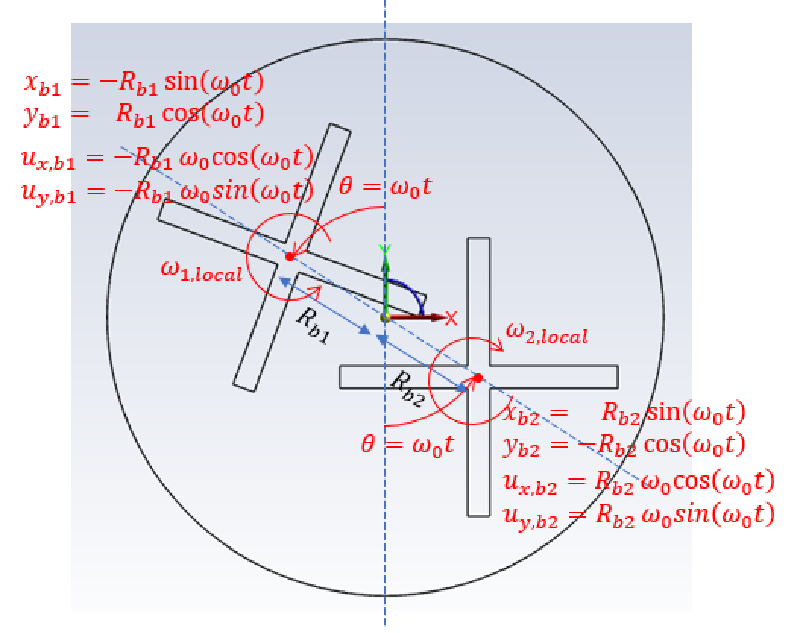
４枚羽の回転ブレード（パドル翼）が二組あり、それらが回転する支持機構の上に設置されているような構造となっている。従って、３種類の回転速度が必要である。回転方向および回転角速度[rad/sec]は図に示す通りである。 $\omega_2$のみが逆方向に回転している。 blade1とblade2の回転半径は相互干渉する位置になっているが、回転位相差があるため、羽は衝突しないで回転するようになっている。

モデル

今回の計算では流体に色をつけてその分布を追跡した。解析領域の下半分に赤色マーカ（UDS=1)を設定するようにした。 UDS変数は移流により移動すると仮定した。 UDS変数の輸送方程式は以下である。

$$ \rho \frac{D S}{D t} = \rho \left(\frac{\partial S}{\partial t} + u_j\frac{\partial S}{\partial x_j} \right)= 0 $$

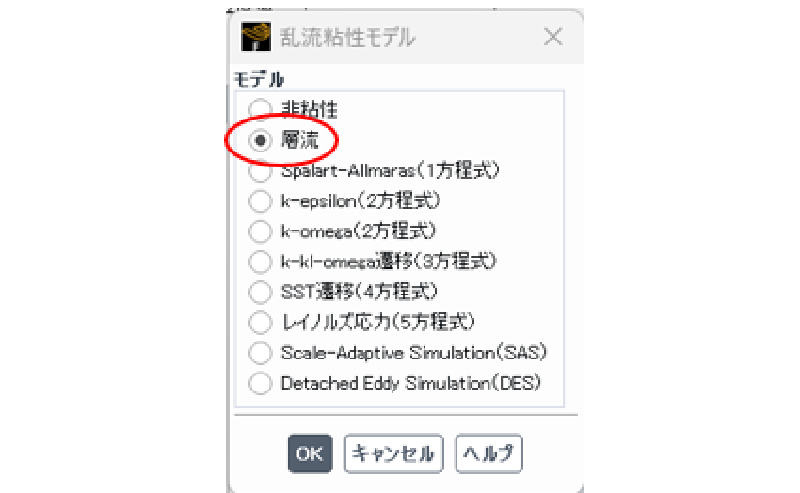
粘度モデル

流れ場は層流であるとした。

粘度モデル

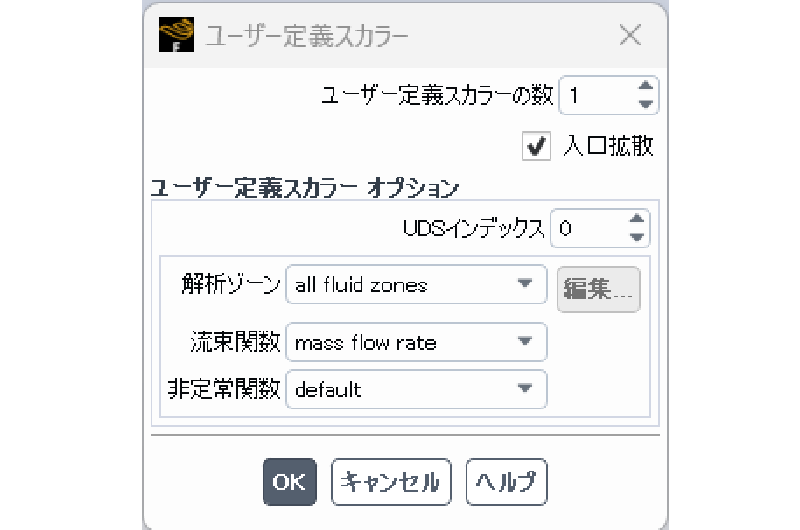
ユーザ定義変数

流れ場の計算に伴ってUDS変数も計算する。 UDS変数は流れの影響を受けるが、UDSから流れに影響を及ぼすことはない（すなわちパッシブスカラーとして扱う）。

uds指定

uds指定2

メッシュ分割

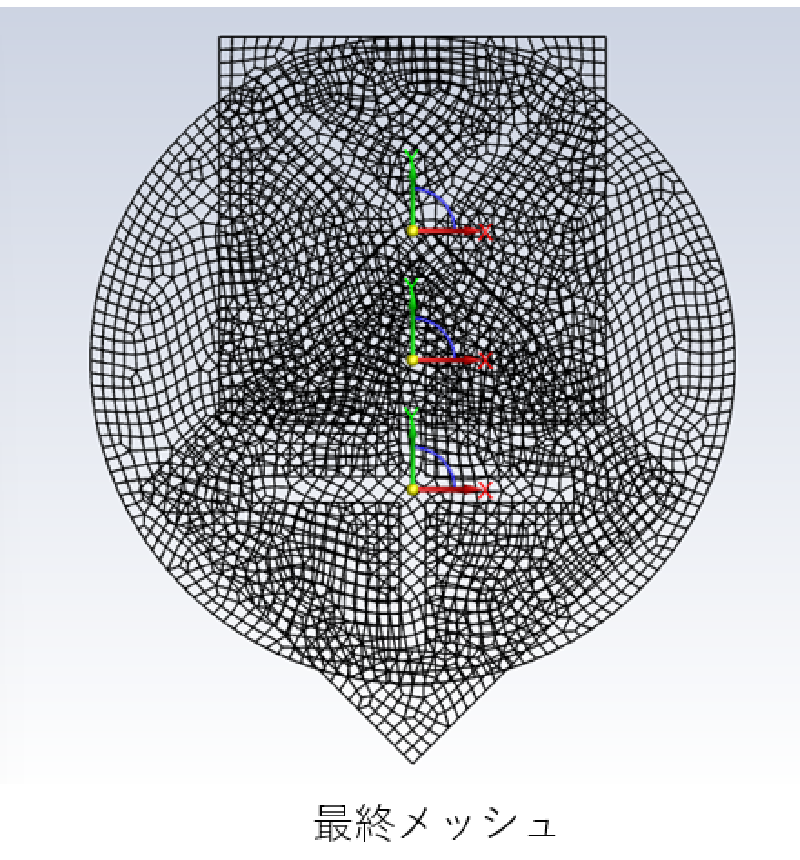
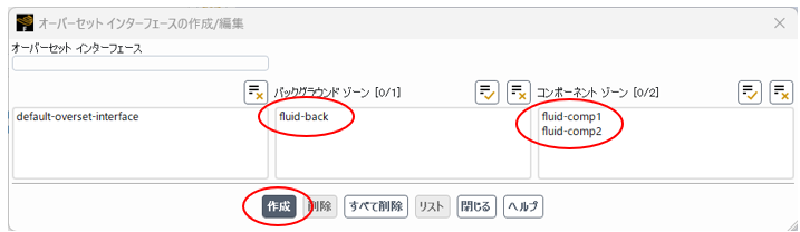
オーバーセット法では、解析領域（back, blade1, blade2)を別々に作成し、それらを結合して最終メッシュを作成している。複数のメッシュを読み込む場合、2個目以降は、”ケースファイルを追加”ボタンを使用する。

mesh-files

add-case-file

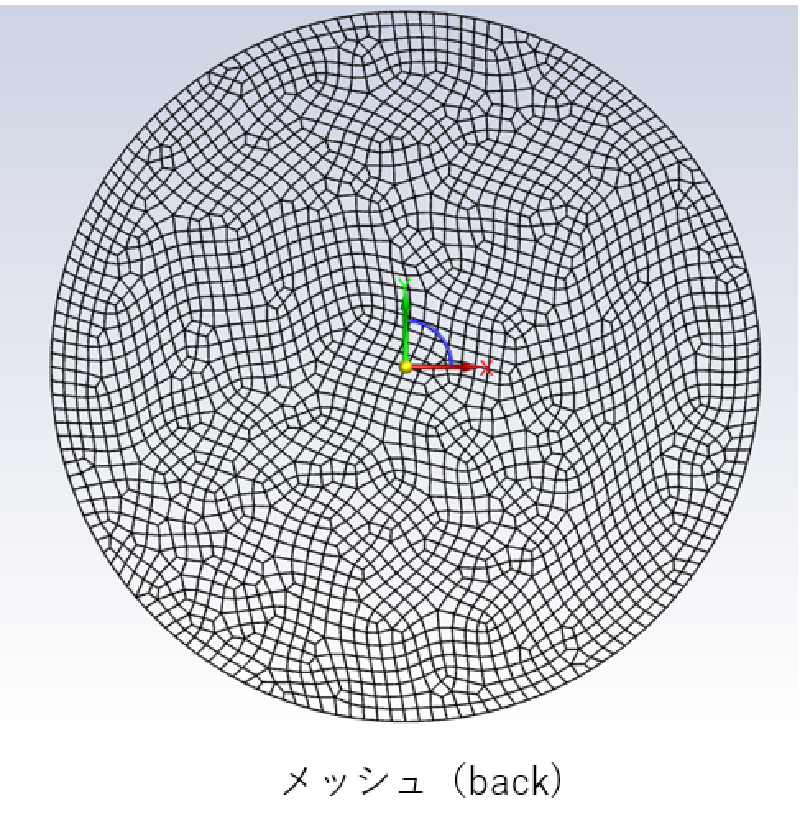
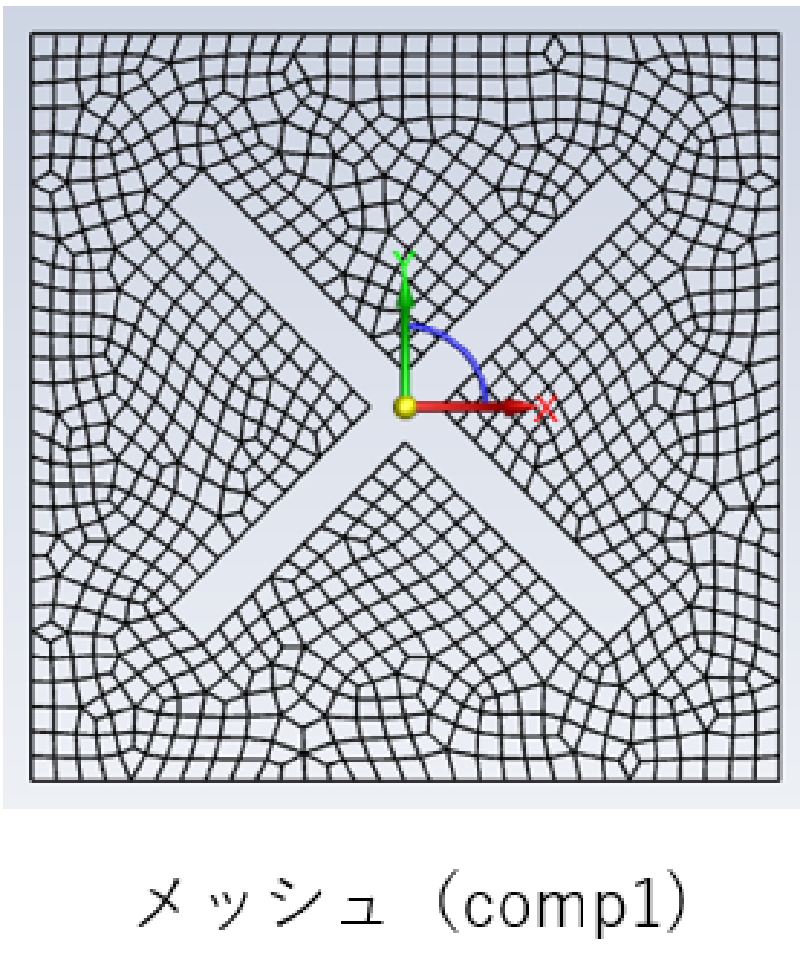
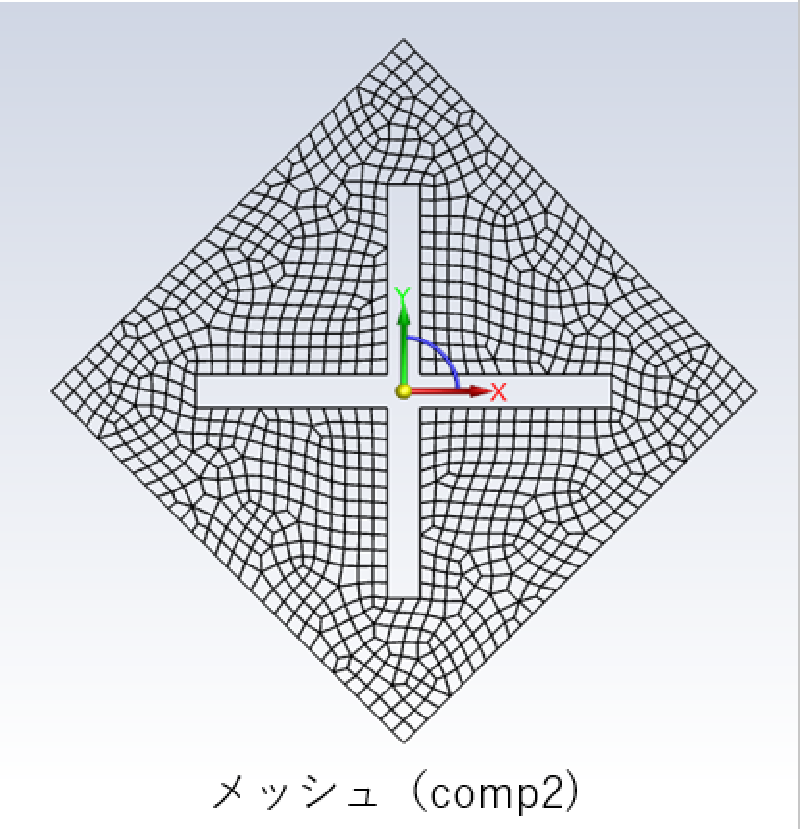
部分ごとに作成したメッシュおよび最終の全体メッシュを示す。

mesh-back

mesh-comp1

mesh-comp2

mesh-final

GUI画面上のリボンのインターフェイスメニューからオーバーセットを選択し、背景メッシュ（back)および成分メッシュ(comp1,comp2)を選択してオーバーセットインターフェイスを定義する。

overset-ribon

インターフェイス

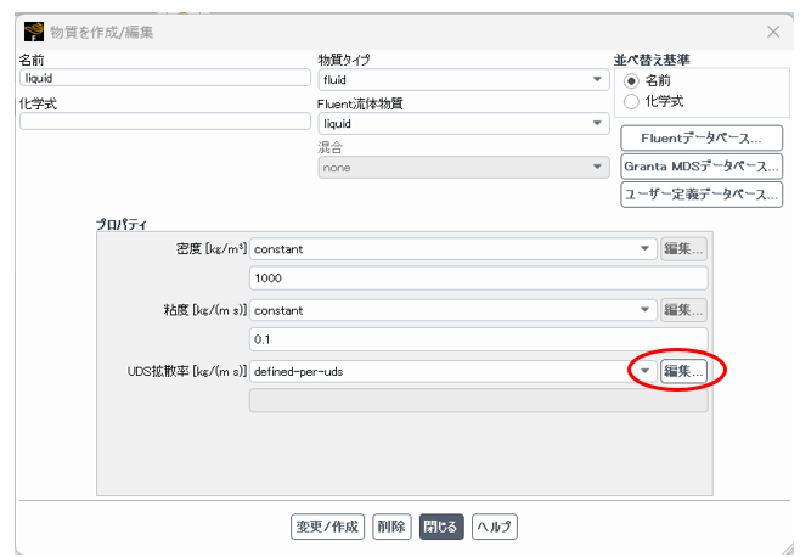
物性値

ここでは以下に示す物性値を仮定した。

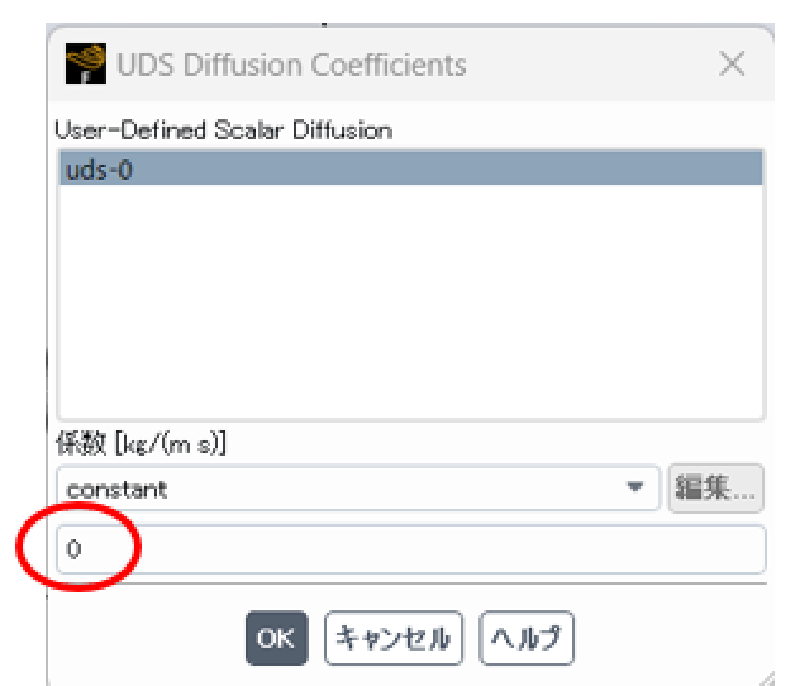
なおUDS変数は移流効果のみにより移動することから拡散係数をゼロとした。

物性値1

物性値2

セルゾーン条件

ブレードの回転の効果はダイナミックメッシュの設定（UDF指定）を使って定義するため、セルゾーン条件を設定する必要はない。

境界条件

ブレードの回転の効果はダイナミックメッシュの設定（UDF指定）を使って定義するため、境界条件を設定する必要はない。固体壁は全て速度ゼロのままにしておく（移動メッシュに属している境界は自動的に移動速度が適用される）。

ダイナミックメッシュ

UDFの記述

オーバセット法では、メッシュ（固体境界）の運動はUDFを使って指定することになる。

使用する関数はDEFINE_CG_MOTIONである。以下にUDFのソースプログラム(fl-overset.c)を示す。

#include "udf.h"

#define RADI    0.2
#define OMG0    1.0
#define OMG1    1.0
#define OMG2   -1.0

/************************************************************/
DEFINE_CG_MOTION(blade1,dt,vel,omega,time,dtime)
/************************************************************/
{
   real theta;

   theta = OMG0*time;

   vel[0] =-RADI * cos(theta) * OMG0;
   vel[1] =-RADI * sin(theta) * OMG0;
   vel[2] = 0;

   omega[0] = 0;
   omega[1] = 0;
   omega[2] = OMG0 + OMG1;
}


/************************************************************/
DEFINE_CG_MOTION(blade2,dt,vel,omega,time,dtime)
/************************************************************/
{
   real theta;

   theta = OMG0*time;

   vel[0] = RADI * cos(theta) * OMG0;
   vel[1] = RADI * sin(theta) * OMG0;
   vel[2] = 0;

   omega[0] = 0;
   omega[1] = 0;
   omega[2] = OMG0 + OMG2;
}

関数の引数の説明は以下の通りである。

引数	内容
blade(1,2)	fluent内での関数表示名
dt	ダイナミックメッシュ属性の構造体ポインター
vel	線速度
omega	角速度
time	現在時刻
dtime	時間ステップ

今回の解析モデルにおける注意点を以下に示す。

velは成分メッシュ(comp1, comp2)の回転中心座標の運動を記述する。
- blade1の場合 $$ x_{b1} = -R_{b1}*sin(\omega_0 t) $$ $$ y_{b1} = R_{b1}*cos(\omega_0 t) $$ $$ u_{x,b1} = \frac{d x_{b1}}{dt}= -R_{b1}*cos(\omega_0 t) *\omega_0 $$ $$ u_{y,b1} = \frac{d y_{b1}}{dt}= -R_{b1}*sin(\omega_0 t) *\omega_0 $$
- blade2の場合 $$ x_{b2} = R_{b2}*sin(\omega_0 t) $$ $$ y_{b2} = -R_{b2}*cos(\omega_0 t) $$ $$ u_{x,b2} = \frac{d x_{b2}}{dt}= R_{b2}*cos(\omega_0 t) *\omega_0 $$ $$ u_{y,b2} = \frac{d y_{b2}}{dt}= R_{b2}*sin(\omega_0 t) *\omega_0 $$

ここで(comp1, comp2)の回転中心の半径は $$ R_{b1}= R_{b2}=0.2 \hspace{0.2cm} m$$ である。

omega は成分メッシュ(comp1, comp2)の回転角速度を記述する。ここで指定する角速度は、絶対座標系から見た場合の値であることに注意。

$$ \omega_{1,global} = \omega_0 + \omega_{1,local} $$ $$ \omega_{2,global} = \omega_0 + \omega_{2,local} $$

ここで角速度は、以下のようになっている $$ \omega_0 = 1 \hspace{0.2cm} [rad/sec] $$ $$ \omega_{1,local} = 1 \hspace{0.2cm} [rad/sec] $$ $$ \omega_{2,local} = -1 \hspace{0.2cm} [rad/sec] $$

velomega

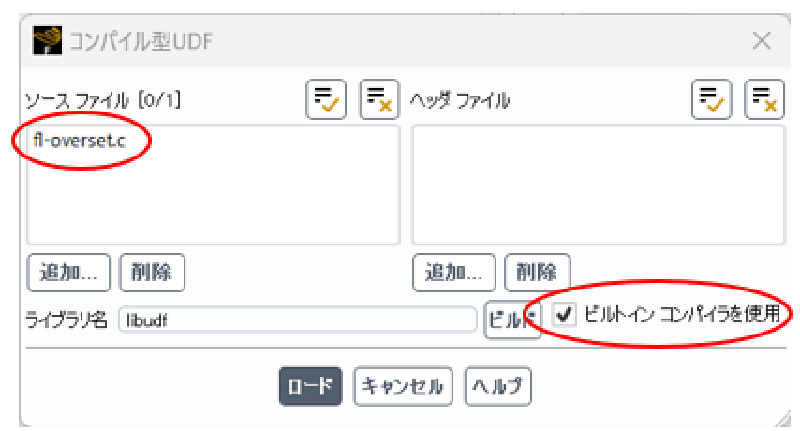
UDFのコンパイル

UDFソースファイル(fl-overset.c)を読み込み、コンパイルリンクする。なおウインドウズの場合、ビルトインをチェックしておく。

udf-compile

入力フォームの指定

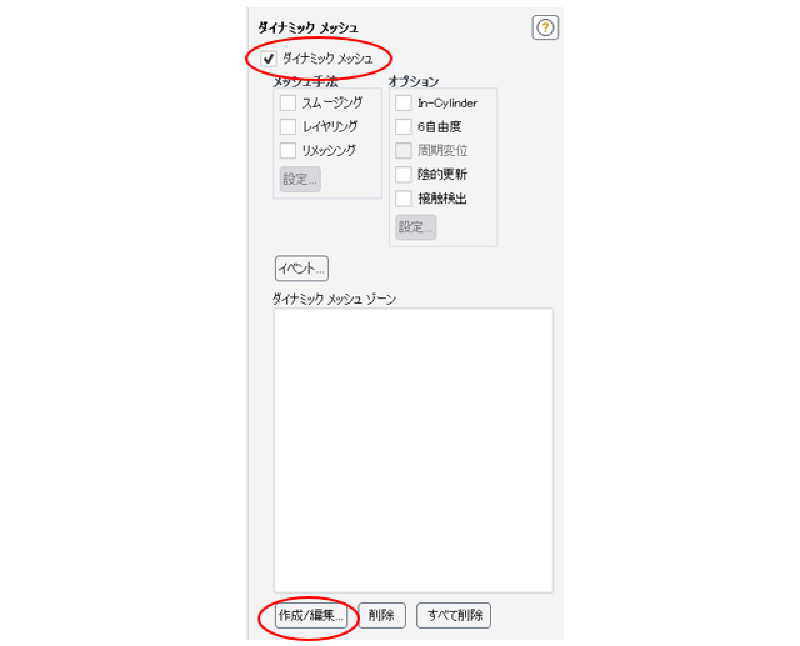
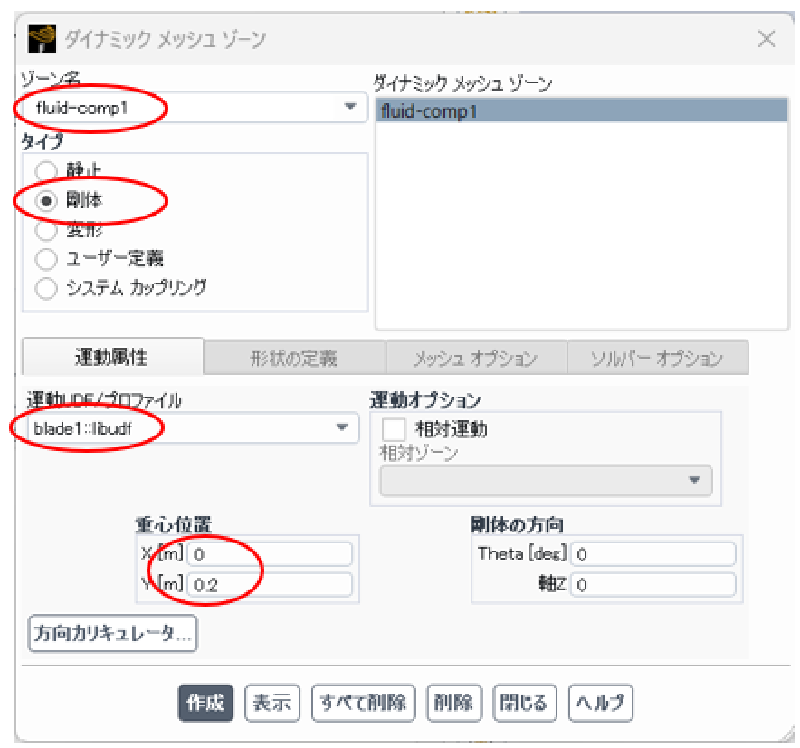
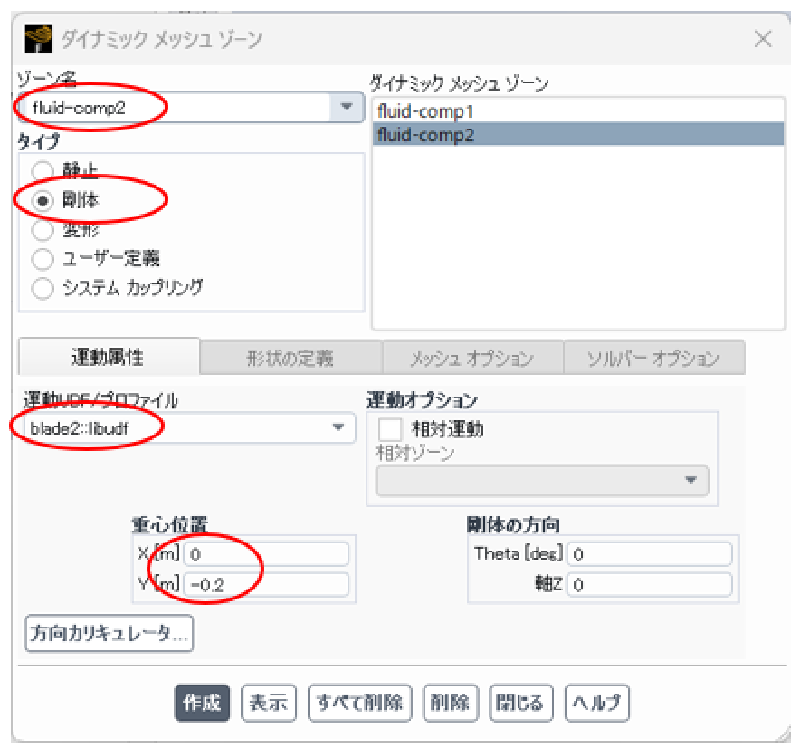
移動するメッシュ（comp1,comp2)は剛体的に移動するのみであるため、メッシュ手法の”スムージング”のチェックは、はずしておく。その後”作成/編集”ボタンを押す。

dynamic

ゾーンfluid-comp1およびfluid-comp2に対して設定を行う。重心位置には、成分メッシュの（初期時刻の）回転中心座標を指定する。

comp1

comp2

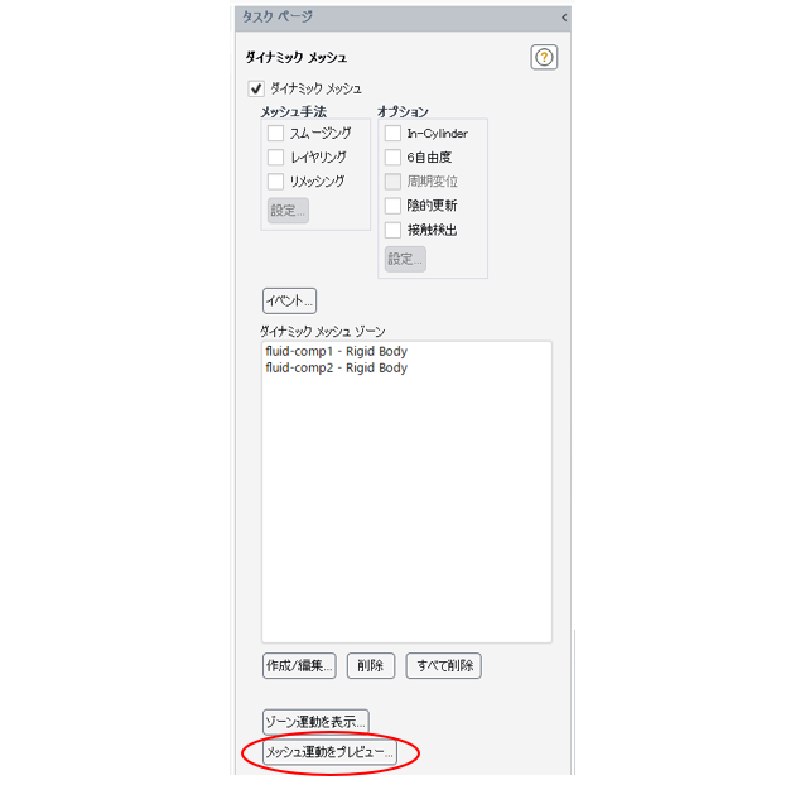
プレビューによるメッシュ移動の確認

本計算に入る前に予めメッシュの運動を画面上で確認することができる。

preview

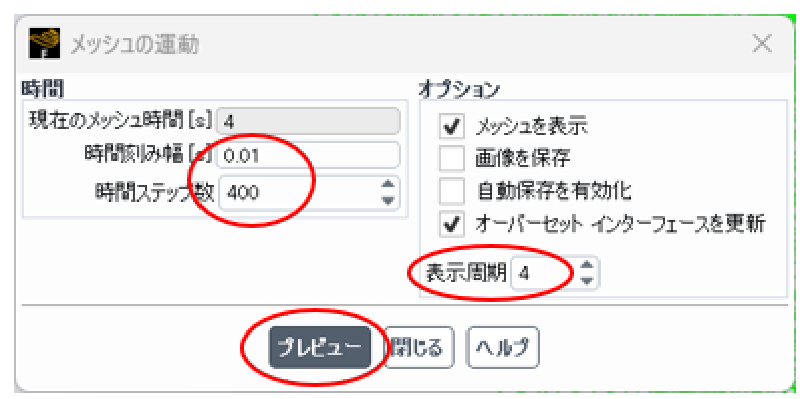
時間刻み幅、ステップ数などを適当に指定する。なお、プレビューを行うとメッシュ位置が更新されてしまうため、予め初期状態をケースファイルに保存するようにしておき、プレビュー確認後に再度ケースファイルを読み込むようにする。

preview2

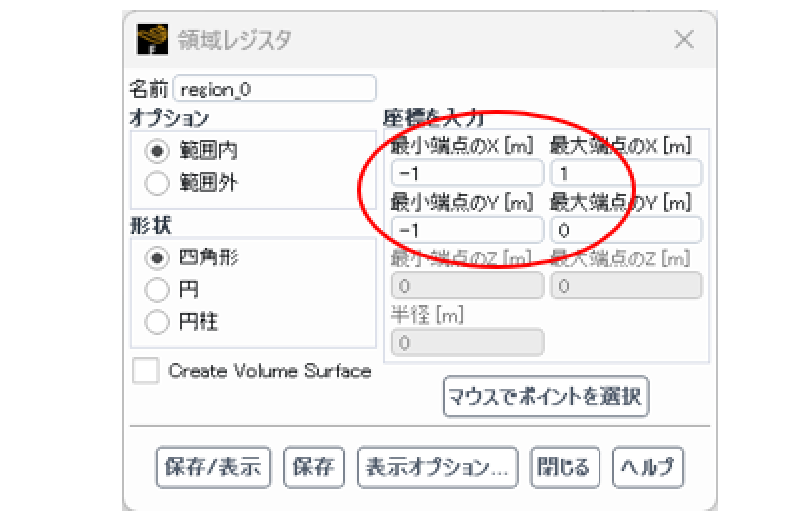
UDS設定ゾーンの作成

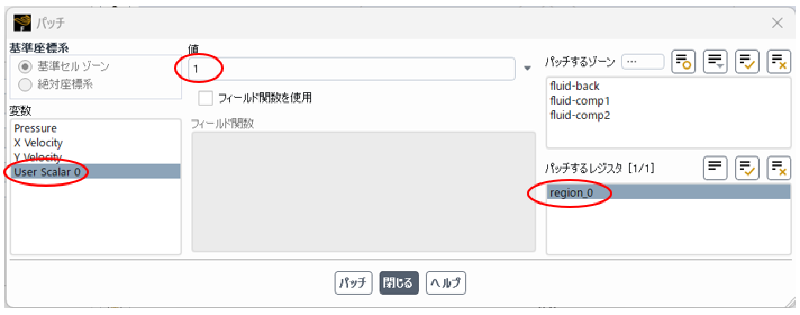
解析領域の下半分においてUDS=1と設定する。まず、ゾーンレジスタを作成する。

レジスタ

レジスタ2

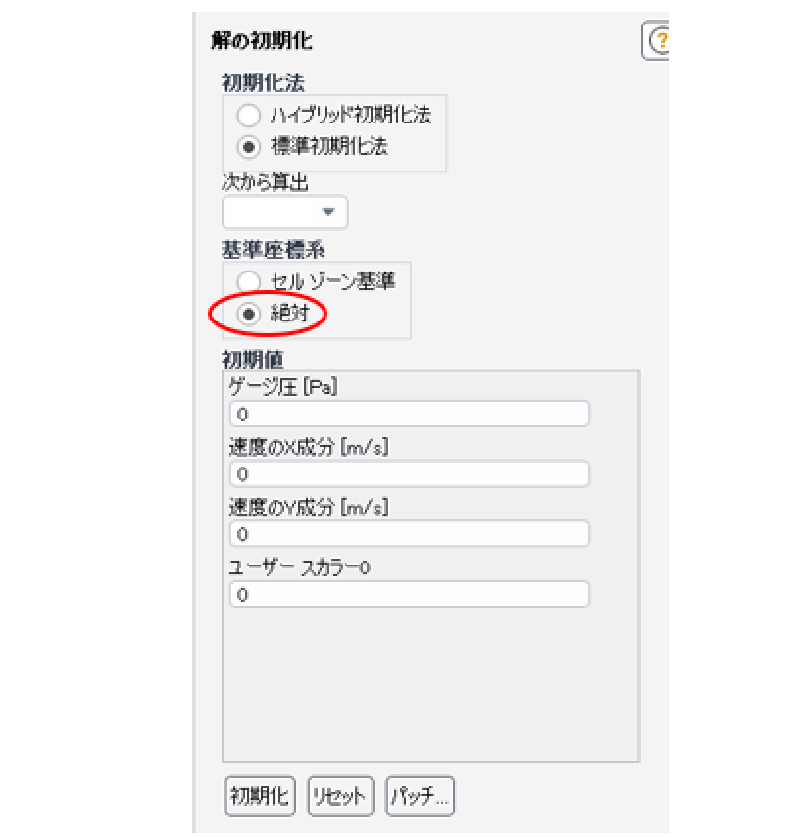
初期化

初期時刻において流速がゼロと指定する（絶対座標系基準）。

初期化

また、パッチを使いUDS変数を指定する。

初期化2

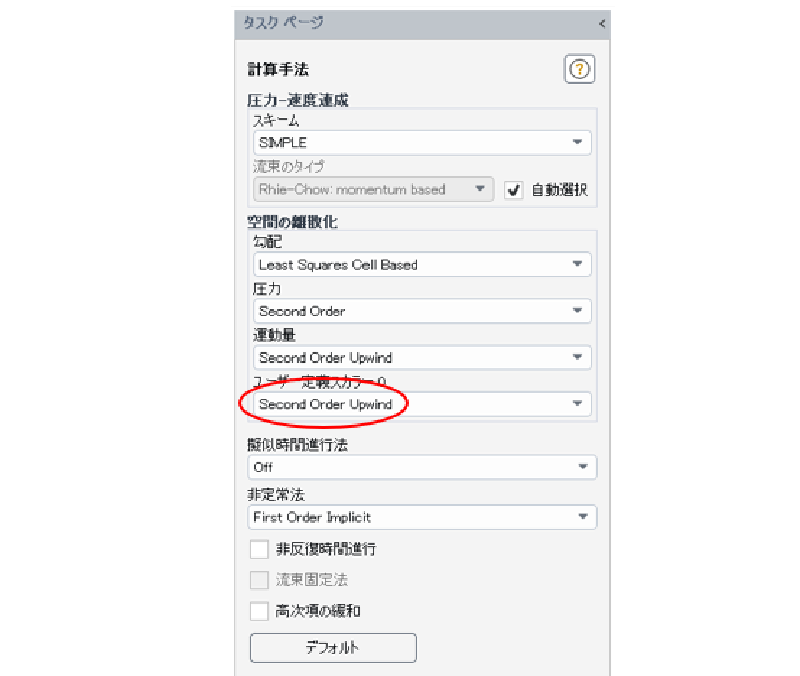
計算手法

UDSの移流項は二次精度風上法で離散化する。

計算手法

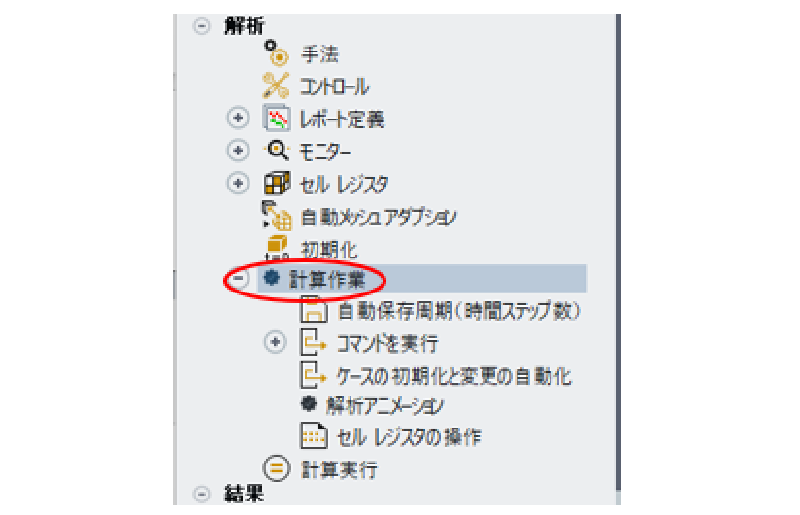
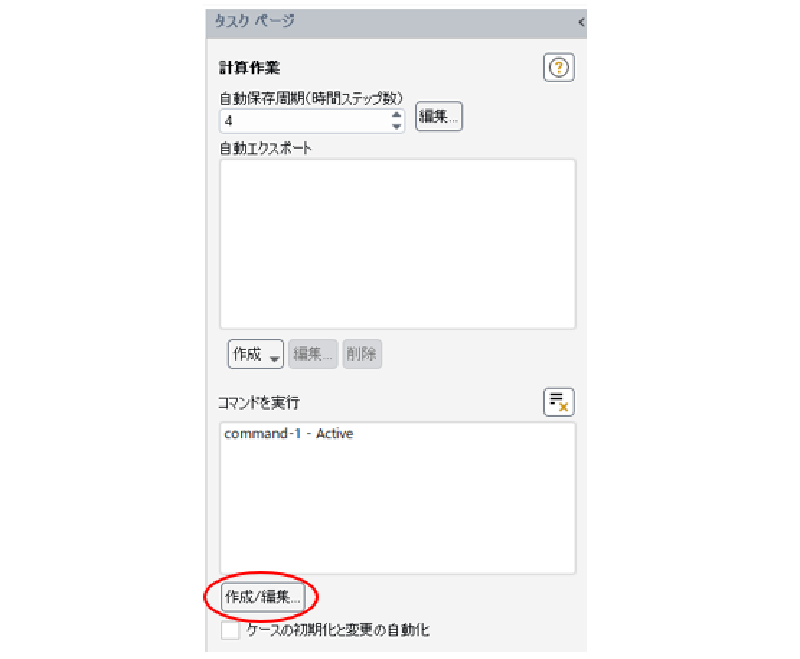
計算作業の設定

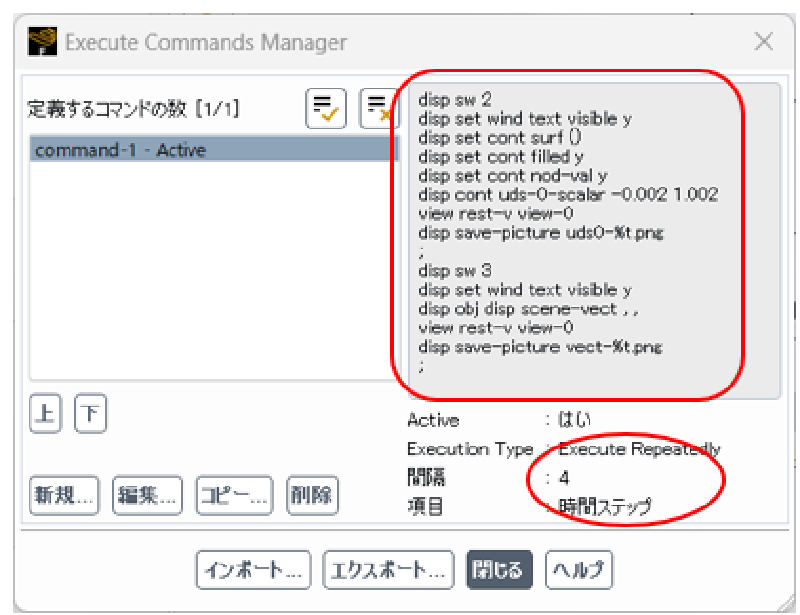
解析の進行に合わせて、リアルタイムで計算結果を画面に表示してそれを画像ファイルとして保存するようにする。以下のように設定を行う。

解析作業

コマンド実行

コマンドの定義にはfluentのTUIコマンドを使用する。ここではウインドウ２、３にそれぞれUDSスカラーコンター図、流速ベクトル図を表示し、同時にステップ番号をつけた画像ファイルとして保存するようにしている。

コマンド実行2

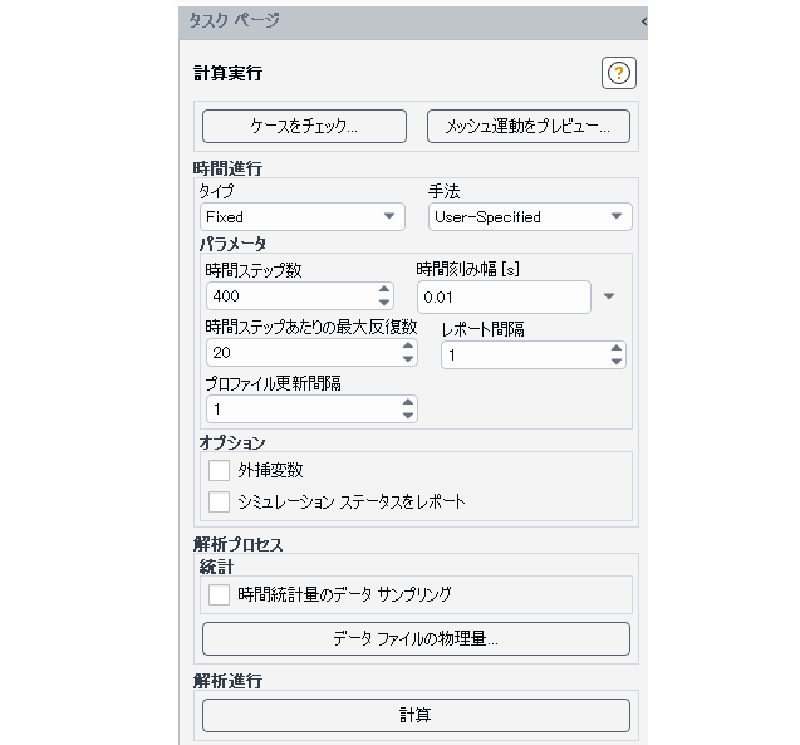
計算実行

時間刻み幅を 0.01 [sec]で400ステップの実行を行った。

実行

計算結果

流速ベクトル

UDSコンター

メッシュ

流速ベクトル

UDSコンター

まとめ

オーバーセット法を使い移動境界問題を計算する手法を紹介した。オーバーセット法では、複数の移動物体ごとに分割してメッシュを作成することができるため、メッシュ作成上の制約は少ない。一方でオーバーセット法では、他の物理モデルと併用できない場合があり、また質量保存の正確性が保証されないなどの問題がある。従って解析対象をよく理解した上で使用することが必要である。

この説明資料が今後の解析の参考になれば幸いである。

弊社の解析事例

弊社の流体解析事例については、下記のリンクからご覧ください．

👉 解析事例のご紹介 FLUENT

👉 流体解析実績及び事例

fluent