粒子層内の水分および熱移動
By M.Sato
土壌内を水分および熱が移動する様子を自作プログラムでシミュレーションしましたので、ご紹介します。
はじめに
土壌は固体粒子、水、空気で構成される複合材料です。
もし土粒子以外の間隙がすべて水で満たされている場合は飽和状態と呼ばれます。
一方間隙内に空気と水が混在している場合は不飽和状態と言われます。

以下では、不飽和状態を対象にして、水分移動、熱移動をシミュレーションした例を示します。
水分移動の基礎方程式
多孔質体内における水分および空気の移動は慣性力の効果を無視できる場合、ダルシーの法則で表されます。
$$ 水分流速:u_l = - \frac{K K_{rl}}{\mu_l}\left (\frac{\partial p_l}{\partial z} - \rho_l g\right) $$
$$ 空気流速:u_g = - \frac{K K_{rg}}{\mu_g}\left (\frac{\partial p_g}{\partial z} - \rho_g g\right) $$
ここで、
$ K:透水係数 [m^2] $
$ K_{rl}, K_{rg}:水分、空気の相対透水係数 [-] $
$ \rho_l, \rho_g:水分、空気密度[kg/m^3] $
$ \mu_l, \mu_g:水分、空気密度 [Pa\cdot s] $
$ p_l, p_g:水分、空気圧力 [Pa] $
空気圧力と水分圧力の差は毛管圧力と呼ばれ、以下で表されます。
$$ p_g - p_l = p_c $$
大気開放系では、$p_g = 0$とみなせることから、水分流速は次式で表現されます。
$$ u_l = \frac{K K_{rl}}{\mu_l}\left (\frac{\partial p_c}{\partial z} + \rho_l g \right) $$
ガス質量が微小で無視できるとすれば、質量保存式は次式で表されます。
$$ \varepsilon \frac{\partial s}{\partial t} = - \frac{\partial u_l}{\partial z} = - \frac{\partial}{\partial z} \left (\frac{K K_{rl}}{\mu_l} \left (\frac{\partial p_c}{\partial z} + \rho_l g \right) \right) $$
ここで、
$\varepsilon$:空隙率、$s$:含水飽和度
を表します。
含水飽和度は空隙中の水分比率を表しています。 相対透水係数$K_{rl}$および毛管圧力$p_c$は土壌中の水分量(すなわち$s$)に依存して変化することから、 この質量保存式は$s’$に関する非線形方程式となっています。
水分特性
相対透水係数$K_{rl}$、および毛管圧力$p_c$に対していくつかの関係式が提案されています。
今回は、下記を採用しました。
$ K_{rl} = s_e^3 $
$ p_c = \frac{\sigma}{\sqrt{\frac{K}{\varepsilon}}} J(s_e) $
$ J(s_e) = 1.417 (1 - s_e) - 2.12(1 - s_e)^2 + 1.263(1 - s_e)^3 $
ここで、$s_e = \frac{s-s_{ir}}{1-s_{ir}}$であり、有効含水飽和度と呼ばれます。 $s_{ir}$は排出不能な限界含水飽和度です。 $J(s_e)$はLeverett関数と呼ばれるものです。
 有効含水飽和度 - 相対透水係数
有効含水飽和度 - 相対透水係数
 有効含水飽和度 - 毛細管圧
有効含水飽和度 - 毛細管圧
熱移動の基礎方程式
土壌は、固体粒子、水、空気から構成されているが各位置において温度が等しいと仮定します(局所平衡)。
エンタルピーの保存式は次式で表されます。
$$ \frac{\partial}{\partial t}\left [(\rho c_p)_T T \right ] = $$
$$ \frac{\partial}{\partial z}\left (\lambda \frac{\partial T}{\partial z}\right) -\frac{\partial}{\partial z}(\rho_l c_{pl} u_l T) $$
$$ (\rho c_p)_T = $$
$$ \rho_s c_{ps}(1 - \varepsilon) + \rho_l c_{pl} \varepsilon s $$
熱伝導率には、固相、液相、気相からなる粒子層の有効熱伝導率が適用されます。
ここでは、ガラス-水系で含水飽和度$s$の関数とした幾世橋らの式を使用しました。
$$ \lambda = \frac{0.8}{1 + 3.78 \exp(-5.95\cdot s)} $$
 飽和度 - 熱伝導率
飽和度 - 熱伝導率
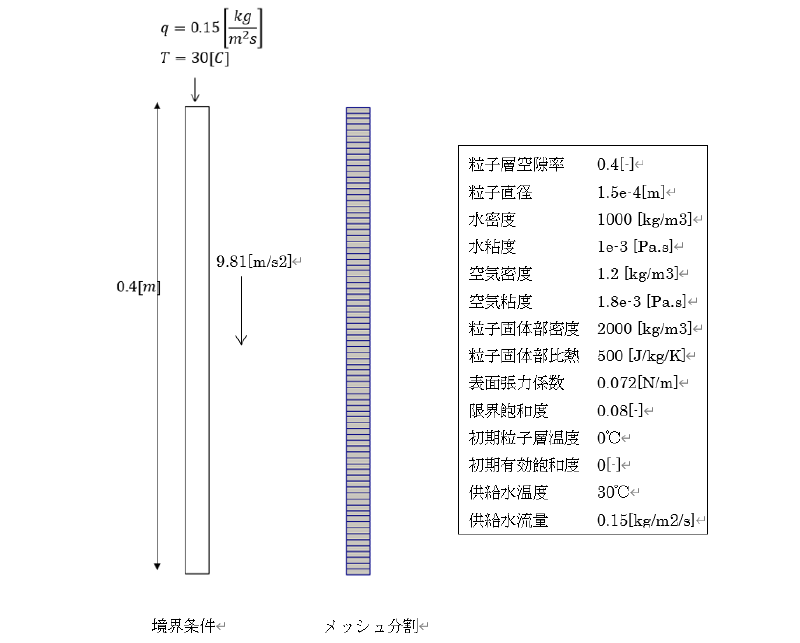
1次元モデルの計算例
粒子層(多孔質体)内を2つの非混合流体の片方が、他方に浸透していく問題は一般に Buckley-Leverett問題と呼ばれています。
一次元モデルを使いBuckley-Leverett問題を計算した例を示します。 これは土壌表面から水分が浸透する様子をシミュレーションした例です。
鉛直方向の飽和度分布および温度分布を示します。
内部への水分移動に比べて温度上昇が遅れていますが、 これは上流部での熱交換により徐々に水分の温度が低下し、 移動前面での熱交換量が少なくなるためです。
 鉛直方向の飽和度分布
鉛直方向の飽和度分布
 鉛直方向の温度分布
鉛直方向の温度分布
 含水飽和度コンター(200,600秒後)
含水飽和度コンター(200,600秒後)
 温度コンター(200,600秒後)
温度コンター(200,600秒後)
 ダルシー流速ベクトル(200,600秒後)
ダルシー流速ベクトル(200,600秒後)
動画
含水飽和度コンター
温度コンター
ダルシー流速ベクトル
弊社のソルバー開発
弊社では、さまざまなソルバーを開発した実績がございます。
ソルバー開発に関する、お問い合わせやご相談等は、こちらからお寄せください。
👉 数値解析プログラムのリメイク