フェーズフィールド法について

はじめに

---

液体の中を移動する泡、空気中を落下する液滴など、 異なる２相間の界面が移動していく問題として捉えられる現象は世の中にたくさんあります。

2相間の界面の移動を追跡するために用いられるシミュレーション手法として、 フェーズフィールド（PF）法という手法があるようです。

PF法は、元々は金属材料のミクロ組織形成シミュレーションの分野で発展してきましたが、 最近では数値流体力学や電気化学等幅広い分野で活用されているようです。

今回の記事では、そのPF法について調べて分かったことを説明していこうと思います。

フェーズフィールド変数

---

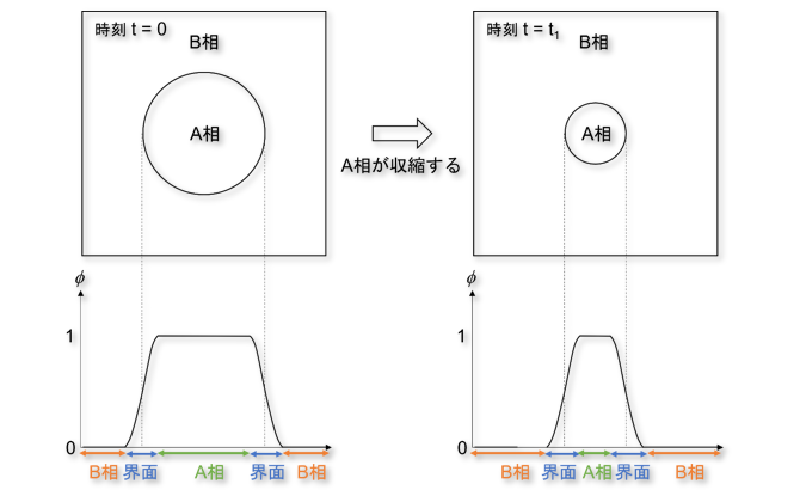
PF法について説明するために、図１に示すA相とB相の２相で構成される系を考えます。

図１　フェーズフィールド変数$\phi$の定義

PF法では、PF変数$\phi(\mathbf{r}, t)$を定義します。 ここで、$\mathbf{r}$は位置、$t$は時刻です。

$\phi(\mathbf{r}, t)$はA相の体積分率を表し、A相の中では$\phi(\mathbf{r}, t) = 1$、 B相の中では$\phi(\mathbf{r}, t) = 0$の値を取ります。

また、A相とB相の界面では$\phi(\mathbf{r}, t)$は$1$から$0$まで滑らかに変化します。 $\phi(\mathbf{r}, t)$が滑らかに変化する領域を界面と定義するため、界面が幅を持つことになります。 これを拡散界面といいます。

PF法では拡散界面を用いるため、界面を滑らかに表現することが可能となり、 界面の曲率を精度よく評価することができます。

実際、図１に示す円形の境界をPF変数と、A相では$1$の値をとり、B相では$0$の値をとる二値変数で表現すると、 図２のようになります。

図２　PF変数と二値変数で表現された界面の比較

二値変数で表現すると界面が階段状になりますが、PF変数では滑らかに表現できていることが確認できます。

いま、$t = 0$で図１の左上図の状態にあったのが、$t = t_1$まで時間が経過してA相が収縮し 図１の右上図の状態になったとします。

このときの$\phi(\mathbf{r}, t)$の分布は図１右下図のようになります。

図１の左下図と右下図を比較すると、$\phi(\mathbf{r}, t)$が滑らかに変化する領域が移動していることが分かります。

このように、PF法では、$\phi(\mathbf{r}, t)$の分布の時間変化を計算するだけで界面の移動を追跡することができます。

系の全自由エネルギー

---

PF変数の時間発展方程式は、系の全自由エネルギーが時間とともに単調減少するという過程のもとで導出されます。 したがって、PF変数を用いて系の全自由エネルギー$G$を構築する必要があります。

一般に、異なる相の界面は、相内部と比較して余剰なエネルギーを有するため、 界面の余剰エネルギーをPF変数により表現することを考えます。

PF法では、PF変数を滑らかに変化する領域を界面と定義するため、 次式のようにPF変数の勾配$\nabla\phi$を二乗した項$g_{grad}$で界面の余剰エネルギーを表すことができます。

$$ g_{grad} = \frac{a^2}{2}|\nabla\phi|^2 $$

$g_{grad}$を勾配エネルギー密度と呼び、係数$a$は勾配エネルギー係数といいます。

PF法では、系の全自由エネルギーが減るように$\phi$が変化するため、$g_{grad}$により空間のあらゆる点で勾配が$0$となります。

すると、仮にA相とB相が同じ割合だけ初期に存在していた場合、$\phi$はどこでも$\phi = 0.5$となり、 A相とB相が混ざり合った状態となってしまいます。

これを防ぐために、次式で表されるダブルウェルポテンシャルと呼ばれる項を導入します。

$$ g_{doub} = W q(\phi) $$

ここで、$W$はエネルギー障壁の高さ、$q(\phi)$はダブルウェル関数であり、次式で与えられます。

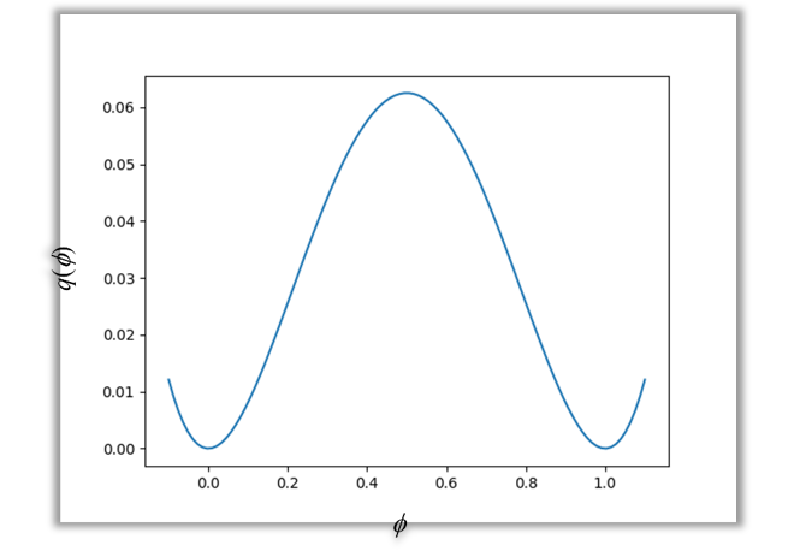
$$ q(\phi) = \phi^2(1-\phi)^2 $$

$q(\phi)$の分布は図3のようになり、$\phi = 0.5$で極大値を取り、$\phi = 0, 1$で極小値を取ります。

図３　ダブルウェル関数のグラフ

これにより、$\phi = 0, 1$の各相が独立した状態が安定となるため、 各相が混ざり合うのを防ぐことができます。

勾配エネルギー密度には界面領域におけるPF変数の勾配を緩やかにする作用があり、 ダブルウェルポテンシャルにはPF変数の勾配を急峻にする作用があります。

両者のバランスによって、PFシミュレーションにおいて界面が安定に存在することが可能となります。

最後に、化学的自由エネルギー密度$g_{chem}$を次式で定義します。

$$ g_{chem} = p(\phi) g_A + (1 - p(\phi)) g_B $$

ここで、$g_A$と$g_B$はそれぞれA相とB相の化学的自由エネルギー密度を表します。 $p(\phi)$は、A相の比率を表す関数です。

上式は、ある点での化学的自由エネルギー密度は各相の存在比率に応じて各相の化学的自由エネルギー密度の 加重平均を取れば得られることを表しています。

以上から、系の全自由エネルギー$G$は次式で表されます。

$$ G = \int_V (g_{chem} + g_{grad} + g_{doub}) dV $$

フェーズフィールド変数の時間発展方程式

---

前節で述べた通り、PF変数の時間発展方程式は系の全自由エネルギー$G$が時間とともに 単調減少するという定理から導出されます。

PF変数が非保存量のとき、時間発展方程式はAllen-Cahn方程式で与えられ、次式で表されます。

$$ \frac{\partial \phi}{\partial t} = - M_\phi \frac{\delta G}{\delta \phi} $$

PF変数が保存量のとき、時間発展方程式はCahn-Hilliard方程式で与えられ、次式で表されます。

$$ \frac{\partial \phi}{\partial t} = \nabla \cdot \left [M_\phi\left (\nabla\frac{\delta G}{\delta \phi}\right) \right] $$

$M_\phi$は界面の移動速度に影響するパラメータであり、フェーズフィールドモビリティと呼ばれます。 $G$は汎関数であるため、汎関数微分を用いています。

フェーズフィールド法による計算例

---

PF法は元々金属材料のミクロ組織形成シミュレーションの分野で発展した手法であるため、 金属の凝固、多結晶粒成長、拡散相変態などへの適用例が多いです。

図４は、PF法を用いてAl-Cu合金の凝固のシミュレーションを行った結果です¹。

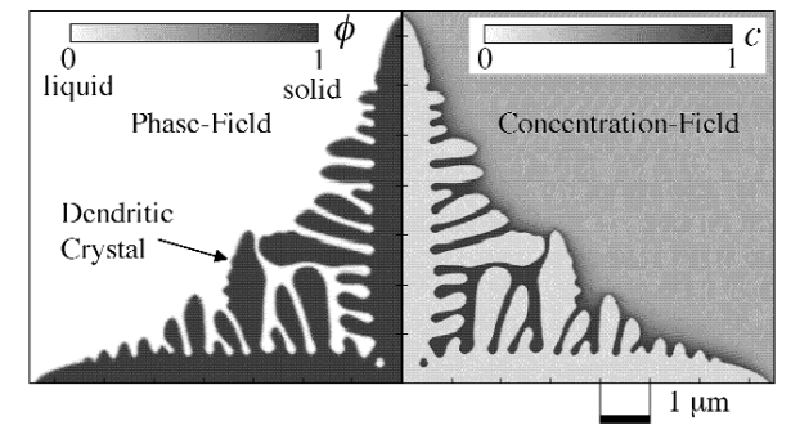図４　Al-Cu合金の凝固のフェーズフィールドシミュレーション¹

このシミュレーションでは、PF変数の時間発展方程式と拡散方程式を連立して解いています。

金属の凝固では、デンドライトと呼ばれる樹枝状の結晶が形成されるため、 固液界面の形状が非常に複雑となりますが、PF法によりデンドライトの成長を再現できていることが分かります。

図５に、マルチフェーズフィールド（MPF）法による鉄鋼材料のオーステナイト・フェライト変態の シミュレーション結果を示します²。

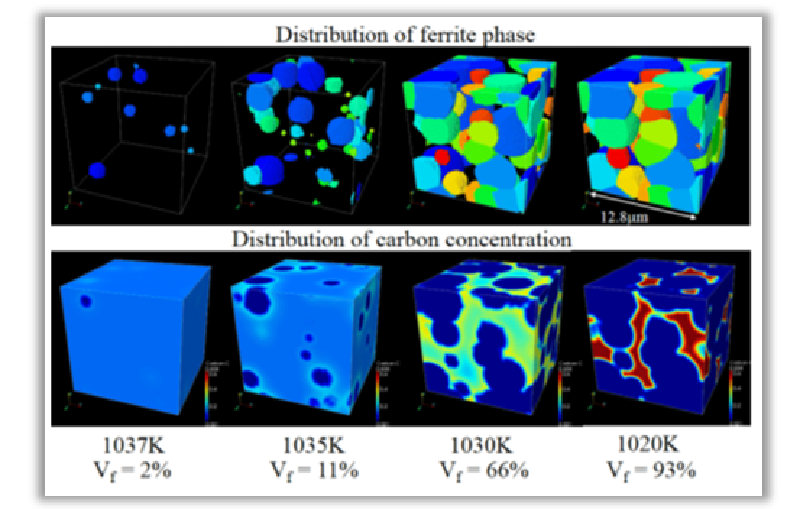図５　鉄鋼材料のオーステナイト・フェライト変態のマルチフェーズフィールドシミュレーション²

ここで、MPF法は、複数のPF変数を扱えるようにPF法を拡張した手法です。

このシミュレーションでは、PF変数の時間発展方程式と炭素濃度の拡散方程式を連立して解いています。

フェライト相がオーステナイト相を侵食しながら成長する過程が再現されています。

PF法は数値流体力学への適用も進んでいます。 その例として、図６に蒸気泡の成長過程のPF法によるシミュレーション結果を示します³。

図６　蒸気泡の成長過程のフェーズフィールドシミュレーション³

このシミュレーションでは、PF変数の時間発展方程式とナビエ・ストークス方程式および 熱伝導方程式を連立して解いています。

左図がシミュレーション結果、右図が実験結果で、シミュレーションにより蒸気泡（黒い部分）が 次第に大きくなっていく過程を再現できていることが分かります。

弊社の解析事例

弊社の流体解析事例については、下記のリンクからご覧ください．

👉 解析事例のご紹介 FLUENT

👉 流体解析 実績及び事例

• フェーズフィールド法