pyfluentを使ったパラメトリック解析
By M.Sato
概要
pyfluentというpythonモジュールを使うことでpythonからfluentを実行可能であることは、以前のブログ記事においていくつか紹介した。
pyfluentは、現在活発に開発が進められておりgithubレポジトリを見ると ほぼ毎日更新されていることがわかる。 pythonスクリプトの記述も徐々に洗練されて来ており、以前よりはかなり使いやすくなっている。
💡 本記事の内容
pyfluentを使いパラメトリックに変数を変えて計算を行い、 その結果に基づきエネルギー損失の応答曲面を作成した例を示す。
⚠️ 注意
現在、pyfluent-parametricのAPIは非推奨となっておりpyfluent-coreにその機能が含まれるようになっている。 今回の解析ではpyfluentのパラメータ解析用のAPI(
solver.settings.file.parametric_project)は使わないで python内で直接複数ケースの計算を行うようにした。
パラメトリック解析
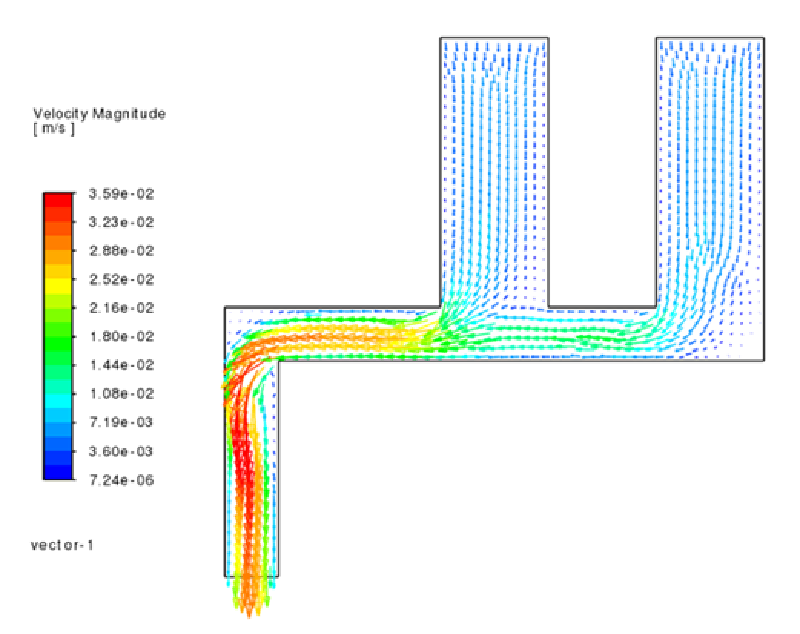
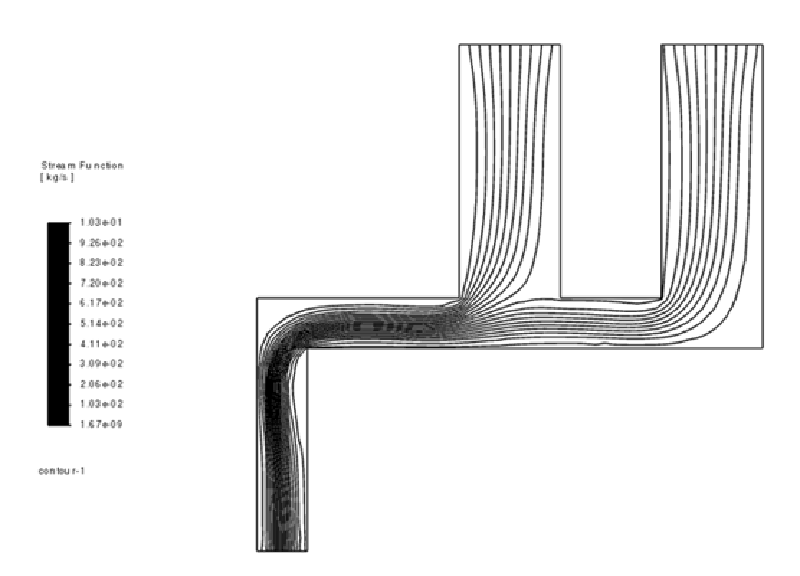
2つの流入口から流入した流体が合流して一個の流出口から流出する流れ場を想定した。
🎯 目的: 流体エネルギーの損失が最も小さくなるようなケースを求める
解析モデル
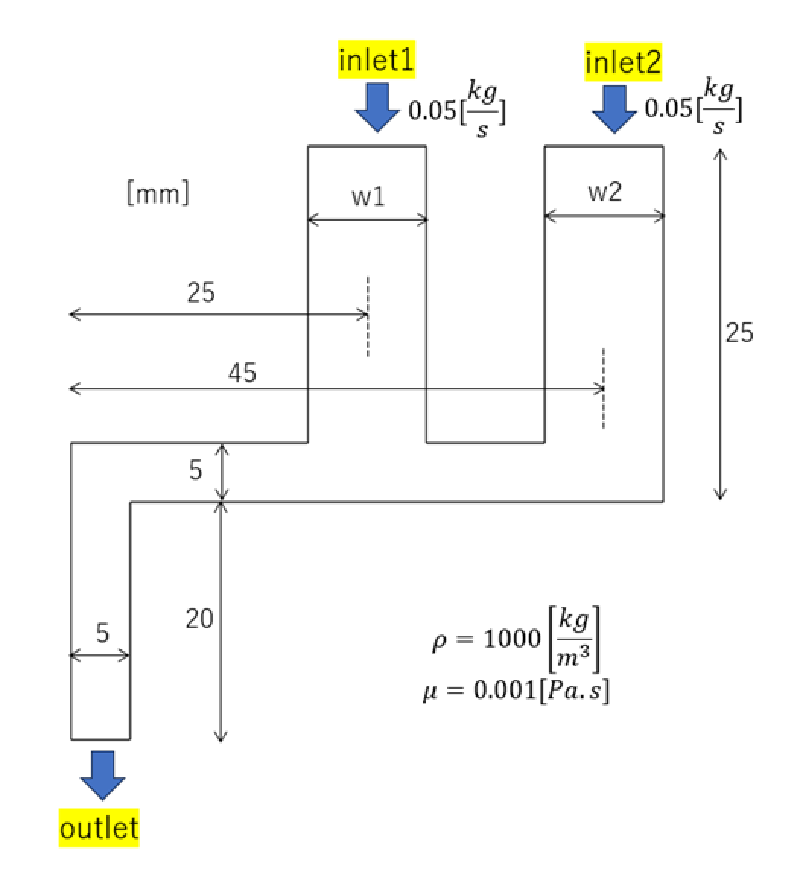
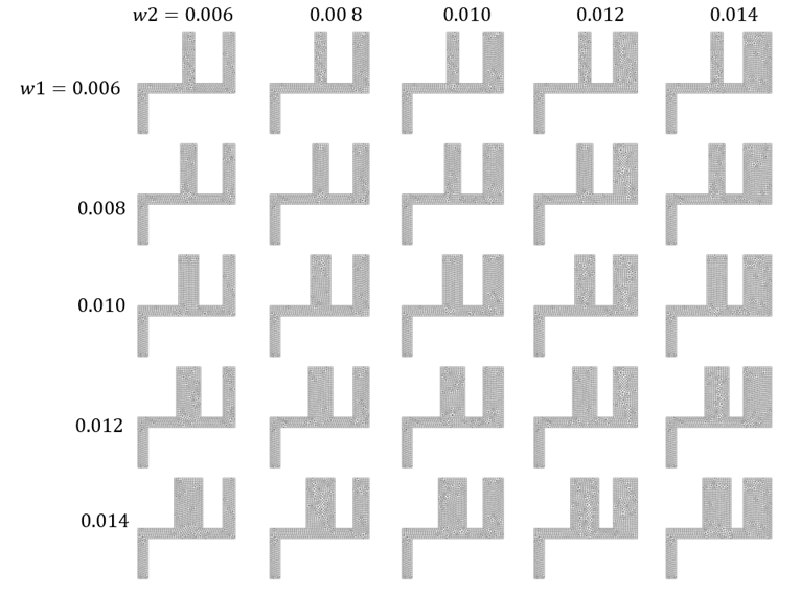
代表的な形状(w1=0.01, w2=0.01)を使い解析モデルを示す。
⚙️ 解析条件
- パラメータ: 図中の$w1, w2$が変化させる寸法
- 流入量: 2つの流入境界からそれぞれ$0.05[kg/s]$(全ケース共通)
物性値
🧪 流体物性値
- 密度: $\rho=1000[kg/m^3]$
- 粘度: $\mu=0.001[Pa.s]$
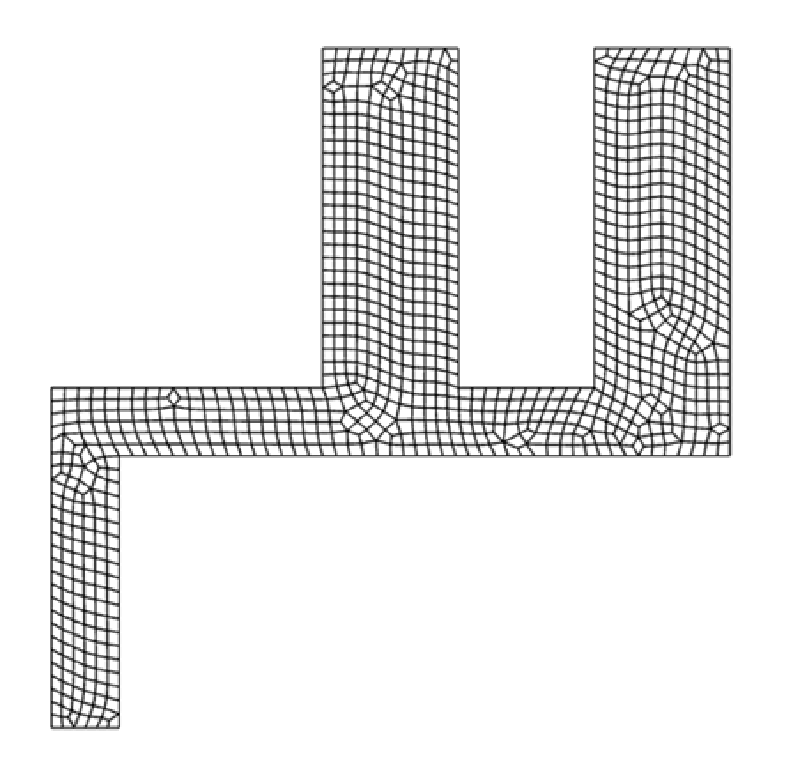
メッシュ作成
メッシュは、fluentに付属したメッシャーではなくgmshを使用して作成した。
ℹ️ gmshを使うメリット
2次元モデルであれば、簡単なgmshコマンドのスクリプトを記述すればfluentのライセンスを気にしないでメッシュを作成することができる。
🔄 メッシュ変換のワークフロー
gmshから直接fluentで読み込み可能なメッシュは作成できないため:
- gmshでnastranのバルクデータ形式(
.bdf)で出力- fluentに読み込んで流体解析用に修正
後述のpythonスクリプトにgmshをpythonから呼び出す関数(create_mesh())を示している。
(流出入境界は形状作成で定義したcurveのタグ番号で区別している)。
⚠️ gmshは予めインストールしておく必要があることに注意。
作成したメッシュの例を示す。
目的関数の定義
機械エネルギーフラックス
流体の持っているエネルギーは流路を通過する際に低減する。
⚡ 評価方法
流出入境界における機械エネルギーフラックス(mechanical energy flux)を評価し、 その差分が損失したエネルギーとみなして損失が最小となる条件を推定した。
$$ \begin{align} mechanical_energy_flux = \left( \frac{1}{2} v^2 + \frac{p}{\rho} \right) v_n \end{align} $$
ここで$v$は流速、$p$は圧力、$\rho$は密度である。
エネルギー損失
2つの流入境界と一個の流出境界における機械エネルギーフラックスを$Q_{in1},Q_{in2},Q_{out}$とし、次式で評価関数を定義した。
📊 目的関数の意味
全流入エネルギーと全流出エネルギーの差を全流入エネルギーで割り正規化したもの。 この評価関数が小さいほど装置を通過する際のエネルギー損失が小さい。
$$ \begin{align} objective_function = \frac{(Q_{in1}+Q_{in2}-Q_{out})}{Q_{in1}+Q_{in2}} \end{align} $$
パラメータ空間
ここでは2つの流入境界の幅 $w1,w2$をパラメータとし、それぞれ以下の5個の値を取ることができるとした。
ℹ️ 計算ケース数
実験計画法に基づき計算ケースを決めることも可能であるが、計算コストは微小であるため全数を計算。 従って全計算ケースは 5×5=25ケース。
w1Arr = np.array([0.006, 0.008, 0.010, 0.012, 0.014])
w2Arr = np.array([0.006, 0.008, 0.010, 0.012, 0.014])
解析結果
全ケースの計算を一括して実施する pythonスクリプト(response_surface.py)を作成し、計算を実施した。
✅ 自動化された処理
- 各計算ケースの収束状況は自動的にログファイルに保存
- 流出入境界におけるエネルギーフラックスはcsvファイルとして自動作成
✅ 収束確認: 全ての計算ケースが約70回の反復回数で収束
代表的な計算ケース($w1=0.01,w2=0.01$)の結果を示す。
 せん断速度コンター(流路幅が小さい箇所でせん断速度大となる)
せん断速度コンター(流路幅が小さい箇所でせん断速度大となる)
応答曲面
応答曲面(目的関数)のコンター図を作成するために plot_object.pyというpythonスクリプトを実行し、コンター図を作成した。
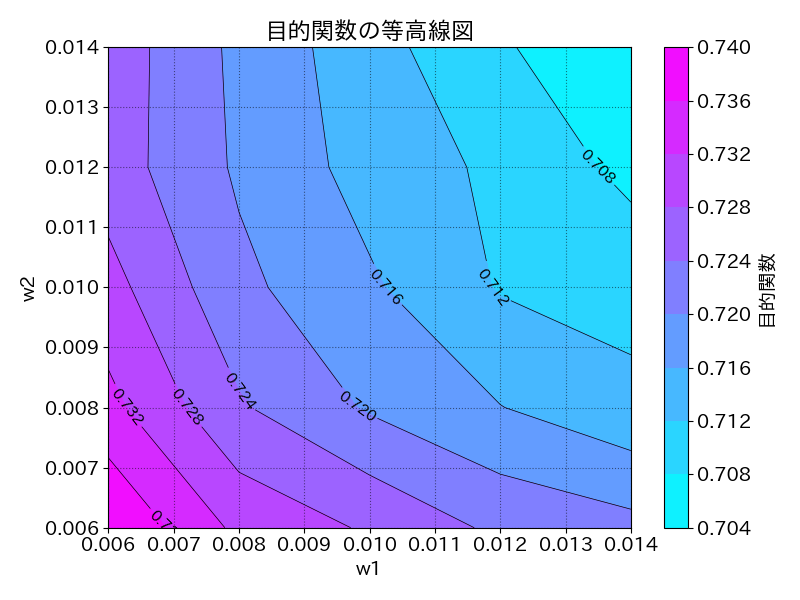
🏆 最適解
この応答曲面を見ると図の右上(w1=w2=0.014)においてエネルギー損失が最小となっていることがわかる。
🔍 考察
エネルギー損失は粘性による摩擦力が流体粒子を変形させることが要因となっていると思われる。 前出のせん断速度コンター図より、流入境界の流路幅が大きいほどエネルギー損失が小さくなっているものと推定される (エネルギー損失 ~ せん断発熱 ~ $せん断速度^2$)。
解析に使用したプログラム
以下に解析に使用したpythonスクリプトおよび目的関数の等高線をプロットするpythonスクリプトを示す。
パラメトリック解析用のスクリプト(response_surface.py)
import numpy as np
import ansys.fluent.core as pyfluent
#-----------------------------------------------------------------------------------
def create_mesh(c1,w1,c2,w2):
#-----------------------------------------------------------------------------------
import gmsh
lc = 0.001;
x1, x2 = 0.00, 0.005
x3 = c1 - w1/2.0
x4 = c1 + w1/2.0
x5 = c2 - w2/2.0
x6 = c2 + w2/2.0
y1, y2, y3, y4 = 0.00, 0.02, 0.025, 0.05
gmsh.initialize()
gmsh.model.add("mymesh")
gmsh.model.geo.addPoint( x1 , y1, 0, lc, 1);
gmsh.model.geo.addPoint( x2 , y1, 0, lc, 2);
gmsh.model.geo.addPoint( x2 , y2, 0, lc, 3);
gmsh.model.geo.addPoint( c1 , y2, 0, lc, 4);
gmsh.model.geo.addPoint( x6 , y2, 0, lc, 5);
gmsh.model.geo.addPoint( x6 , y4, 0, lc, 6);
gmsh.model.geo.addPoint( x5 , y4, 0, lc, 7);
gmsh.model.geo.addPoint( x5 , y3, 0, lc, 8);
gmsh.model.geo.addPoint( x4 , y3, 0, lc, 9);
gmsh.model.geo.addPoint( x4 , y4, 0, lc, 10);
gmsh.model.geo.addPoint( x3 , y4, 0, lc, 11);
gmsh.model.geo.addPoint( x3 , y3, 0, lc, 12);
gmsh.model.geo.addPoint( x1 , y3, 0, lc, 13);
gmsh.model.geo.addLine( 1, 2,11) # outlet
gmsh.model.geo.addLine( 2, 3,12)
gmsh.model.geo.addLine( 3, 4,13)
gmsh.model.geo.addLine( 4, 5,14)
gmsh.model.geo.addLine( 5, 6,15)
gmsh.model.geo.addLine( 6, 7,16) # inlet2
gmsh.model.geo.addLine( 7, 8,17)
gmsh.model.geo.addLine( 8, 9,18)
gmsh.model.geo.addLine( 9,10,19)
gmsh.model.geo.addLine(10,11,20) # inlet1
gmsh.model.geo.addLine(11,12,21)
gmsh.model.geo.addLine(12,13,22)
gmsh.model.geo.addLine(13, 1,23)
gmsh.model.geo.addCurveLoop([11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23],1)
gmsh.model.geo.addPlaneSurface([1], 1)
gmsh.model.geo.mesh.setRecombine(2, 1)
gmsh.model.geo.synchronize()
gmsh.model.mesh.generate(2)
gmsh.model.addPhysicalGroup(2,[1],1) # solid
gmsh.model.addPhysicalGroup(1,[11],2) # outlet
gmsh.model.addPhysicalGroup(1,[20],3) # inlet1
gmsh.model.addPhysicalGroup(1,[16],4) # inlet2
gmsh.write("mymesh.bdf")
gmsh.finalize()
#-----------------------------------------------------------------------------------
def run_fluent(c1,w1,c2,w2):
#-----------------------------------------------------------------------------------
import ansys.fluent.core as pyfluent
import subprocess
###########################################################################
# launch fluent, enable transcript file (trn), import bulkdata
# !caution! since overwriting of trn file is not allowed, they have to be removed beforehand
solver = pyfluent.launch_fluent(
precision="double",
processor_count=1,
version="2d"
)
print(solver.get_fluent_version())
# import bulk data
solver.tui.file.import_.nastran.bulkdata("mymesh.bdf")
trnfile = 'case-{0}-{1}.trn'.format(w1,w2)
solver.tui.file.start_transcript(trnfile)
solver.settings.setup.models.energy = {"enabled": False}
solver.settings.setup.models.viscous.model = "laminar"
###########################################################################
# create material property
solver.settings.setup.materials.fluid["water"] = {
"density": {"option": "constant", "value": 1000},
"viscosity": {"option": "constant","value": 0.001 },
}
###########################################################################
# adjust mesh data so fluid analysis can be performed
# continuum cells are supposed as solid when imported, change to fluid
solver.settings.setup.cell_zone_conditions.set_zone_type(
zone_list=["solid-1"], new_type="fluid"
)
# change boundary name so human can identify easily
solver.settings.setup.boundary_conditions.wall["wall-11"].rename("outlet")
solver.settings.setup.boundary_conditions.wall["wall-20"].rename("inlet1")
solver.settings.setup.boundary_conditions.wall["wall-16"].rename("inlet2")
# change boundary type from "wall" to anything appropriate
solver.settings.setup.boundary_conditions.set_zone_type(
zone_list=["inlet1","inlet2"], new_type="mass-flow-inlet"
)
solver.settings.setup.boundary_conditions.set_zone_type(
zone_list=["outlet"], new_type="pressure-outlet"
)
# assign fluid property to cell zone
solver.settings.setup.cell_zone_conditions.fluid["fluid-1"].material = "water"
# set boundary conditions
inlet1 = solver.settings.setup.boundary_conditions.mass_flow_inlet["inlet1"]
inlet1.momentum.mass_flow_rate.value = 0.05
inlet2 = solver.settings.setup.boundary_conditions.mass_flow_inlet["inlet2"]
inlet2.momentum.mass_flow_rate.value = 0.05
outlet = solver.settings.setup.boundary_conditions.pressure_outlet["outlet"]
###############################################################################
# named expression to calculate mechanical energy flux
solver.settings.setup.named_expressions["ene"] = {
"definition": "StaticPressure/Density+Velocity.mag**2/2"
}
###############################################################################
# solution methods
solver.settings.solution.methods.p_v_coupling.flow_scheme = "SIMPLEC"
solver.settings.solution.methods.spatial_discretization.discretization_scheme[
"pressure"
] = "presto!"
###############################################################################
# Initialize flow field
solver.settings.solution.initialization.initialization_type = "standard"
solver.settings.solution.initialization.standard_initialize()
###############################################################################
# Solve for 300 iterations
solver.solution.run_calculation.iterate(iter_count=300)
file = 'case-{0}-{1}.cas.h5'.format(w1,w2)
# save calculation result
solver.settings.file.write_case_data(file_name=file)
# calculate report
ein1 = solver.scheme_eval.exec(
('(ti-menu-load-string "/report/surface-integrals/flow-rate inlet1 () expr:ene no")',)
).split(" ")[-1]
ein2 = solver.scheme_eval.exec(
('(ti-menu-load-string "/report/surface-integrals/flow-rate inlet2 () expr:ene no")',)
).split(" ")[-1]
eout = solver.scheme_eval.exec(
('(ti-menu-load-string "/report/surface-integrals/flow-rate outlet () expr:ene no")',)
).split(" ")[-1]
dummy = solver.scheme_eval.exec(
('(ti-menu-load-string "/report/surface-integrals/area-weighted-avg inlet1 inlet2 outlet () pressure no")',)
)
dummy = solver.scheme_eval.exec(
('(ti-menu-load-string "/report/surface-integrals/area-weighted-avg inlet1 inlet2 outlet () velo-mag no")',)
)
dummy = solver.scheme_eval.exec(
('(ti-menu-load-string "/report/fluxes/mass-flow no inlet1 inlet2 outlet () no")',)
)
print('ein1={} ein2={} eout={}'.format(ein1,ein2,eout))
solver.tui.file.stop_transcript()
solver.exit()
return ein1,ein2,eout
#-----------------------------------------------------------------------------------
def parametric_survey():
#-----------------------------------------------------------------------------------
w1Arr = np.array([0.006, 0.008, 0.010, 0.012, 0.014])
w2Arr = np.array([0.006, 0.008, 0.010, 0.012, 0.014])
ein1Arr = np.zeros((w1Arr.shape[0], w2Arr.shape[0]))
ein2Arr = np.zeros((w1Arr.shape[0], w2Arr.shape[0]))
eoutArr = np.zeros((w1Arr.shape[0], w2Arr.shape[0]))
for idx1, w1 in np.ndenumerate(w1Arr):
for idx2, w2 in np.ndenumerate(w2Arr):
create_mesh(0.025,w1,0.045,w2)
ein1,ein2,eout = run_fluent(0.025,w1,0.045,w2)
ein1Arr[idx1][idx2] = float(ein1)
ein2Arr[idx1][idx2] = float(ein2)
eoutArr[idx1][idx2] = -float(eout)
with open("inlet1.csv","w") as o:
for row in ein1Arr:
o.write(",".join(map(str, row)) + "\n")
with open("inlet2.csv","w") as o:
for row in ein2Arr:
o.write(",".join(map(str, row)) + "\n")
with open("outlet.csv","w") as o:
for row in eoutArr:
o.write(",".join(map(str, row)) + "\n")
if __name__ == "__main__":
parametric_survey()
目的関数の等高線をプロットするスクリプト(plot_object.py)
import csv
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
w1Arr = np.array([0.006, 0.008, 0.010, 0.012, 0.014])
w2Arr = np.array([0.006, 0.008, 0.010, 0.012, 0.014])
xval = np.zeros((w1Arr.shape[0], w2Arr.shape[0]))
yval = np.zeros((w1Arr.shape[0], w2Arr.shape[0]))
zval = np.zeros((w1Arr.shape[0], w2Arr.shape[0]))
with open('inlet1.csv') as f:
reader = csv.reader(f)
ein1 = [[float(cell) for cell in row] for row in reader]
with open('inlet2.csv') as f:
reader = csv.reader(f)
ein2 = [[float(cell) for cell in row] for row in reader]
with open('outlet.csv') as f:
reader = csv.reader(f)
eout = [[float(cell) for cell in row] for row in reader]
for i in range(len(eout)):
for j in range(len(eout[0])):
xval[i][j] = w1Arr[i]
yval[i][j] = w2Arr[j]
zval[i][j] = (ein1[i][j] + ein2[i][j] - eout[i][j])/(ein1[i][j] + ein2[i][j])
# print(f"zval[{i}][{j}] = {zval[i][j]}")
##################################################################################
plt.rcParams['font.size'] = 14 # グラフの基本フォントサイズの設定
# タイトル名
my_title = f'目的関数の等高線図'
# グラフサイズ
plt.figure(figsize=(8, 6)) # 幅8インチ、高さ6インチ
# 等高線図のプロット
my_split = 10
contour = plt.contour(xval, yval, zval, levels=my_split, linewidths=0.5, colors='k')
contourf = plt.contourf(xval, yval, zval, levels=my_split, cmap='cool') # カラーマップ
# 等高線上に数値をテキストで表示
plt.clabel(contour, inline=True, fontsize=11) # fontsizeを変更
# 軸ラベルの設定
plt.xlabel(f'w1', fontsize=14)
plt.ylabel(f'w2', fontsize=14)
# タイトル
plt.title(my_title)
# カラーバーの追加
plt.colorbar(label="目的関数")
# 薄い点線のグリッドを追加
plt.grid(linestyle='dotted', alpha=0.5, color='k')
# レイアウトを調整
plt.tight_layout()
# グラフの表示
plt.show()
# グラフを画像ファイルで保存
#plt.savefig(f'contour.png')
まとめ
pyfluentを使いパラメトリック解析を行う例を示した。
📋 本解析の成果
✅ pyfluentを使ったパラメトリック解析の自動化に成功
✅ メッシュ作成から解析実行まで一括処理
✅ 効率的なパラメータ調査と応答曲面の作成が可能
弊社の解析事例
弊社の流体解析事例については、下記のリンクからご覧ください.