球形粒子の運動におけるサフマン揚力の効果
By M.Sato
概要
流体中を球形粒子が移動する際に、粒子には様々な流体力が作用している。 ここではサフマン揚力に注目し、どのような特性があるかを調べてみた。
サフマン揚力は流体中に速度勾配が存在する場合に粒子に作用する力である。 簡単のため抗力、浮力、サフマン揚力のみが粒子に作用していると 仮定し、粒子(流体)相、流速分布、粒径などを変えた場合の影響を調べた。調査の結果 以下のようなことがわかった。
- 粒径が極めて小さい場合、粒子緩和時間が極めて小さくなり、 その結果、粒子は流体に追随して移動する。両者の速度差がほぼゼロとなりサフマン揚力はほぼゼロとなる
- 粒径が極めて大きい場合、長さの$3$乗に比例する体積力項が、長さの$2$乗に比例する面積力項よりも支配的となる。 浮力項は前者、サフマン項は後者であり、その結果サフマン揚力の影響は顕著ではなくなる
- 式を見れば明白であるが、サフマン揚力の作用する方向は相対速度$(\mathbf{u}-\mathbf{v})$と渦度$\omega$の外積の方向で決まる
粒子の運動を記述する方程式
流体中を移動する球形粒子の運動方程式は次式で表される1。
$$ \begin{align} \frac{\pi d^3}{6}(\rho_p+C_M \rho) \frac{d \mathbf{v}}{d t} &= \frac{\pi d^3}{6}\rho (1+C_M)\frac{D \mathbf{u}}{D t} \\ & + \frac{1}{8}C_D\pi d^2 \rho |\mathbf{u}-\mathbf{v}|(\mathbf{u}-\mathbf{v}) \\ & + \frac{2}{3}d^2 \sqrt{\pi \rho \mu} \int_{t_0}^{t} \frac{1}{\sqrt{t-\tau}}\left(\frac{D\mathbf{u}}{D\tau}-\frac{d\mathbf{v}}{d\tau}\right)d\tau \\ & + \frac{1}{8} C_L\pi d^2 \rho |\mathbf{u}-\mathbf{v}|\frac{(\mathbf{u}-\mathbf{v})\times \mathbf{\omega}_p}{|\mathbf{\omega}_p|} \\ & + 1.61 C_s d^2 \sqrt{\mu\rho} \frac{(\mathbf{u}-\mathbf{v})\times\mathbf{\omega}}{\sqrt{|\mathbf{\omega}|}} \\ & + \frac{\pi d^3}{6}(\rho_p-\rho)\mathbf{g} \end{align} $$
ここで、
- $d$:粒子径
- $\rho_p$:粒子密度
- $\rho$:流体密度
- $\mu$:流体粘度
- $\mathbf{u}$:流体速、
- $\mathbf{v}$:粒子速度
- $\omega$:渦度$(=\nabla\times\mathbf{u})$
- $\omega_p$:粒子回転速度
- $\mathbf{g}$:重力加速度
- $C_M$:付加質量係数(=0.5)
- $C_D$:抗力係数
- $C_L$:揚力係数
- $C_s$:サフマン揚力の係数 である。
粒子運動方程式の右辺項についてわかりやすいように(1)から(6)までの番号をつけている。 これらの項は、それぞれ、以下の内容を表している。
- (1) 流体の非定常運動に起因する力
- (2) 粒子の周囲を流体が流れることで発生する抵抗力
- (3) バセット項(物体周囲の境界層の発達が時間遅れを伴うことに起因する力)
- (4) マグナス項(粒子の回転に伴って発生する揚力)
- (5) サフマン項(流速勾配がある流れ場で発生する揚力)
- (6) 浮力項(流体と粒子の密度差に起因する力)
サフマン揚力は元々低Re数の流れを想定して導出された表式を、 高Re数流れにも適用できるように、定数$C_s$を使って一般化されたものである。
$C_s$は粒子レイノルズ数($R_{ep}$)の増加とともに減少することが知られている。
今回のシミュレーションでは簡単のため以下の表現式を仮定した。
$$ \begin{align} C_s(R_{ep}) &= exp(-R_{ep}/20) \end{align} $$
数値シミュレーション
粒子運動方程式において左辺項が $d\mathbf{v}/dt$となるように変形すると以下のようになる。
$$ \begin{align} \frac{d \mathbf{v}}{d t} &= \left[ \frac{\rho}{\rho_p}(1+C_M)\frac{D \mathbf{u}}{D t} \right. \notag \\ & \qquad + \frac{\mathbf{u}-\mathbf{v}}{\tau_p} \notag \\ & \qquad + \frac{9}{d \rho_p} \sqrt{\frac{\rho \mu}{\pi}} \int_{t_0}^{t} \frac{1}{\sqrt{t-\tau}}\left(\frac{D\mathbf{u}}{D\tau}-\frac{d\mathbf{v}}{d\tau}\right)d\tau \notag \\ & \qquad + \frac{3}{4d} C_L \frac{\rho}{\rho_p} |\mathbf{u}-\mathbf{v}|\frac{(\mathbf{u}-\mathbf{v})\times \mathbf{\omega}_p}{|\mathbf{\omega}_p|} \notag \\ & \qquad + 9.66 C_s \frac{ \sqrt{\mu\rho}}{\pi d \rho_p} \frac{(\mathbf{u}-\mathbf{v})\times\mathbf{\omega}}{\sqrt{|\mathbf{\omega}|}} \notag \\ & \qquad +\left. \left(1- \frac{\rho}{\rho_p} \right)\mathbf{g} \right] / \left(1+C_M \frac{\rho}{\rho_p} \right) \notag \end{align} $$
ここで、$\tau_p$は粒子緩和時間、$R_{ep}$は粒子レイノルズ数であり以下のように表される。
$$ \tau_p = \frac{\rho_p d^2}{18\mu} \frac{24}{C_D R_{ep}} \\ R_{ep} = \frac{\rho d |\mathbf{u}-\mathbf{v}|}{\mu} $$
以下の解析では、流体慣性力は無し($D\mathbf{u}/Dt=0$)とし、バセット項、マグナス項を除外し、 右辺には抗力項、サフマン項、浮力項のみが含まれるようにした。
粒子相、流体相には水と空気を想定した。これらの物性値は以下の通りである。
| 物性 | 値 |
|---|---|
| 水密度 | $1000 [kg/m^3]$ |
| 水粘度 | $1e$-$3$ [Pa.s]$ |
| 空気密度 | $1.2 [kg/m^3]$ |
| 空気粘度 | $1.8e$-$5$ [Pa.s]$ |
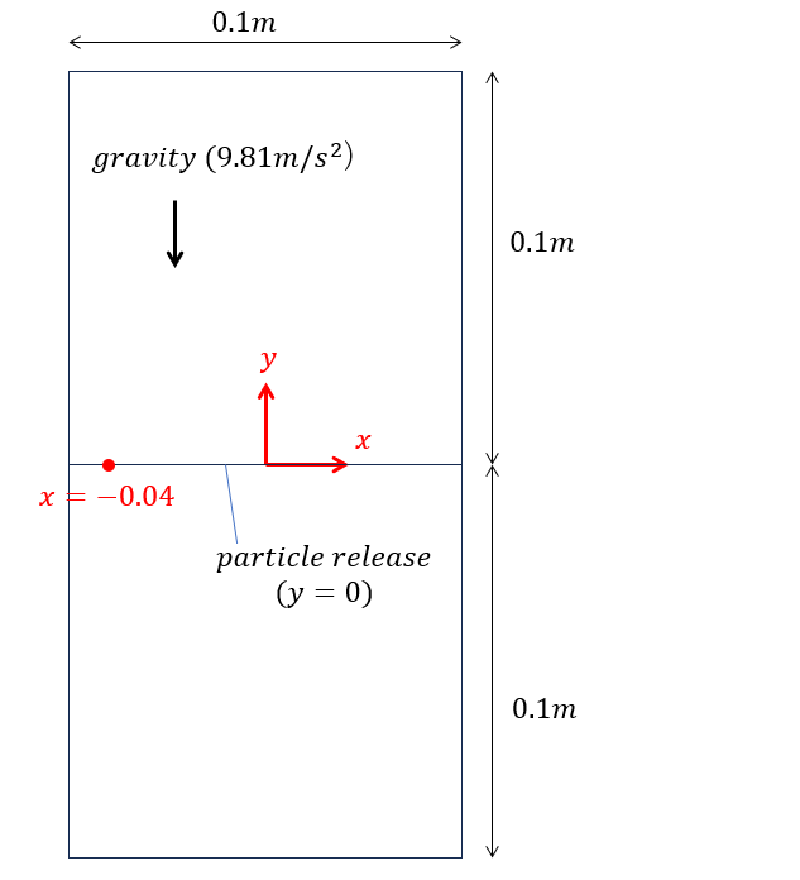
解析範囲は幅 $0.1[m]$の直線流路とし、$y=0$面上の放出点から粒子を放出した。 粒子追跡は$y=+0.1[m]$あるいは $y=-0.1[m]$に到達した時点で停止するようにした。 また側面に衝突した場合は完全反射するようにした。
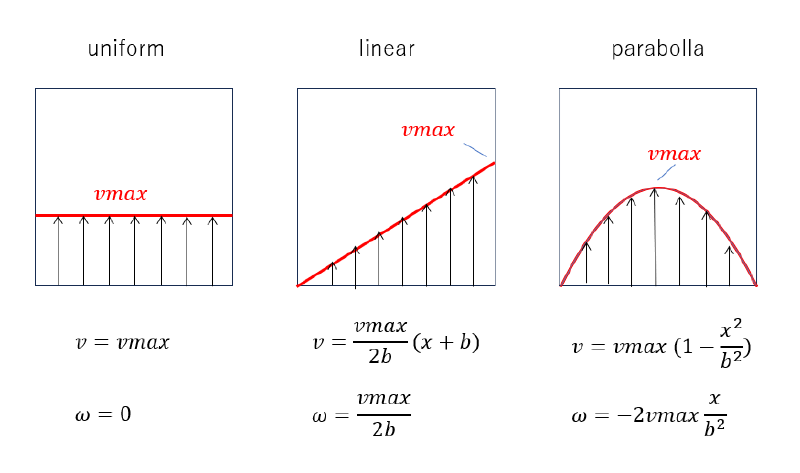
流速分布には以下の$3$種類を想定した。 $vmax$が正の場合、上向き速度、負の場合、下向き速度を表す。 図中には$(x,y)$の関数として表現した流速分布$v$、渦度$\omega$を併記している。
なお、粒子を放出する際の粒子初期速度は全てのケースにおいてゼロとした。
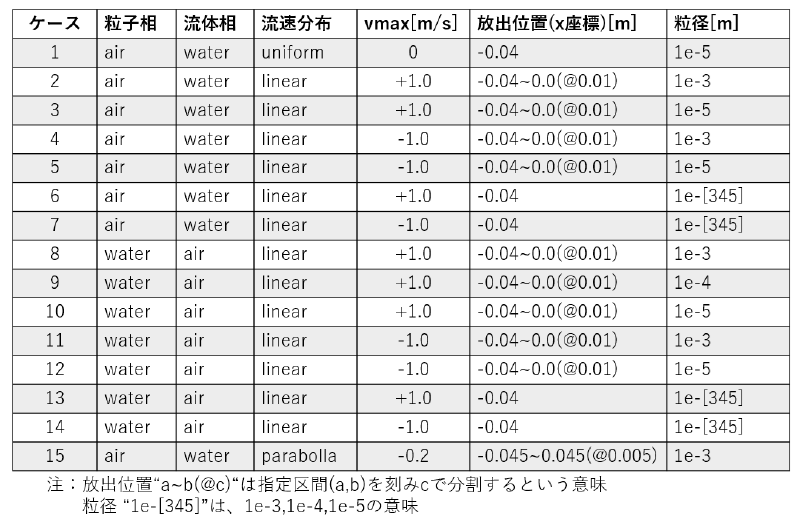
計算ケース
以下に計算ケースの一覧を示す。
計算結果
解析は julia で作成したプログラムを使い実行した。 以下に各ケースの計算結果を示す。
各ケースについて以下の結果図を表示している。
- 粒子軌跡のアニメーション表示(ケースによりグラフの$x,y$軸表示範囲は調整している)
- 粒子位置($xp,yp$)および粒子速度($up,vp$)の経時変化
case-1
このケースは粒子に作用する抵抗力のテストのために実施した。 粒子のストークス抵抗則に基づく終端速度は次式で表される。 これは粒子追跡プログラムで計算された値と一致した。
$$ \begin{align} v_{ternimal} &= \frac{g d^2 (\rho_p - \rho)}{18\mu} \\ &= \frac{-9.81\times10^{-10}\times(1.2-1000)}{18\times 10^{-3}} \\ &=5.443\times10^{-5}[m/s] \end{align} $$
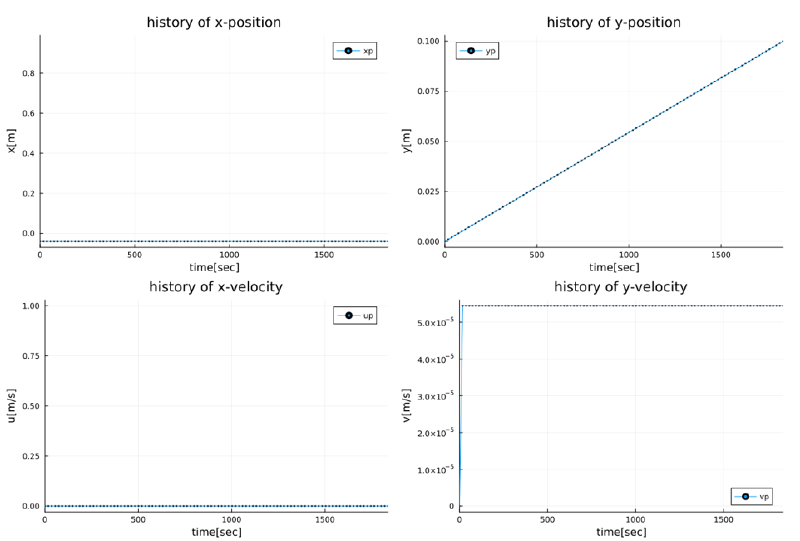
case-2
このケースは空気気泡の粒径が$1e$-$3$と大きいため浮力効果が顕著である。
そのため、相対速度$\mathbf{u}-\mathbf{v}$は下向き($-y$方向)のベクトルとなる。
一方$\omega$は紙面垂直上向きベクトルとなるため、 両者の外積$(\mathbf{u}-\mathbf{v})\times\omega$は$-x$方向のベクトルとなる。
その結果粒子は左側($-x$方向)に移動していることがわかる。
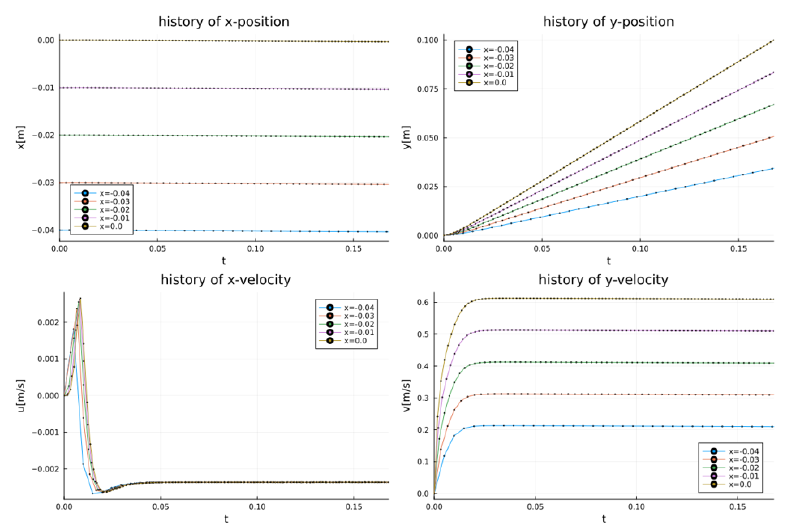
case-3
このケースは空気気泡の粒径が$1e$-$5$と小さいため、 緩和時間が極めて小さく($6.7e$-$9[sec]$)、 その結果、粒子は流体にほぼ追随して移動している。
相対速度がほぼゼロであるためサフマン項のほぼゼロとなっている。
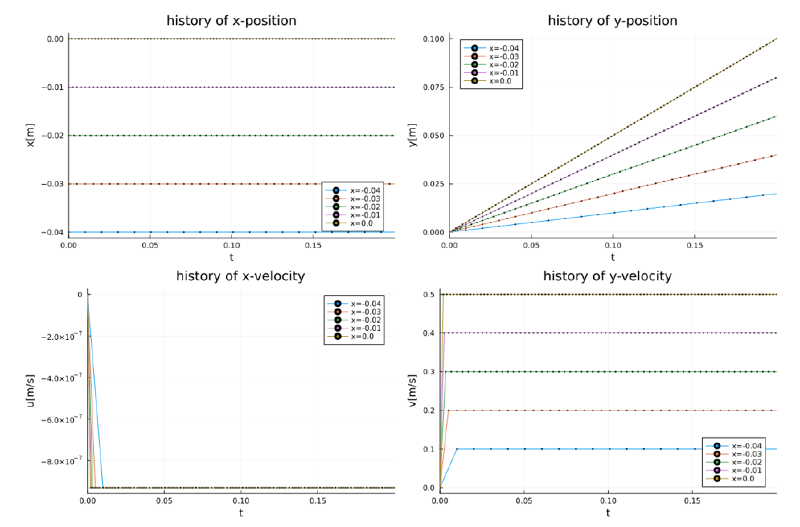
case-4
このケースはcase-2の流速を逆転したものである。 相対速度$\mathbf{u}-\mathbf{v}$は下向きのベクトルとなる。 一方$\omega$は紙面垂直下向きベクトルとなるため、 両者の外積は$+x$方向のベクトルとなる。 その結果粒子は右側($+x$方向)に移動していることがわかる。
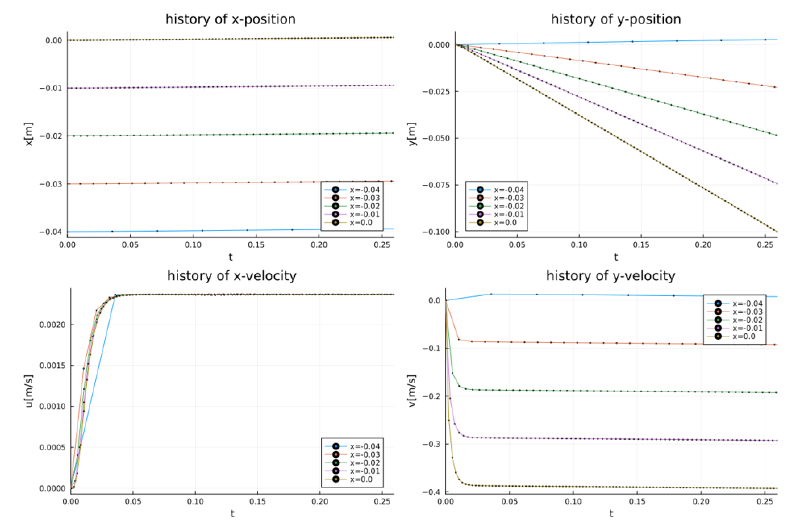
case-5
このケースは粒径が小さいため、case-3と同様にサフマン項はほぼゼロである。
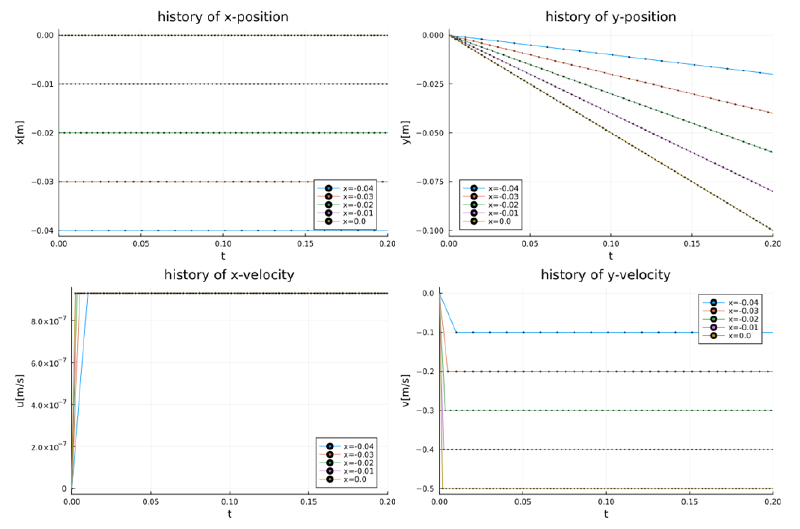
case-6
このケースは粒径の効果を調べたものである。 相対速度が$-y$方向、$\omega$が紙面上向き方向より$-x$方向のサフマン力が発生している。 粒径が大きいほど揚力が顕著となっている。
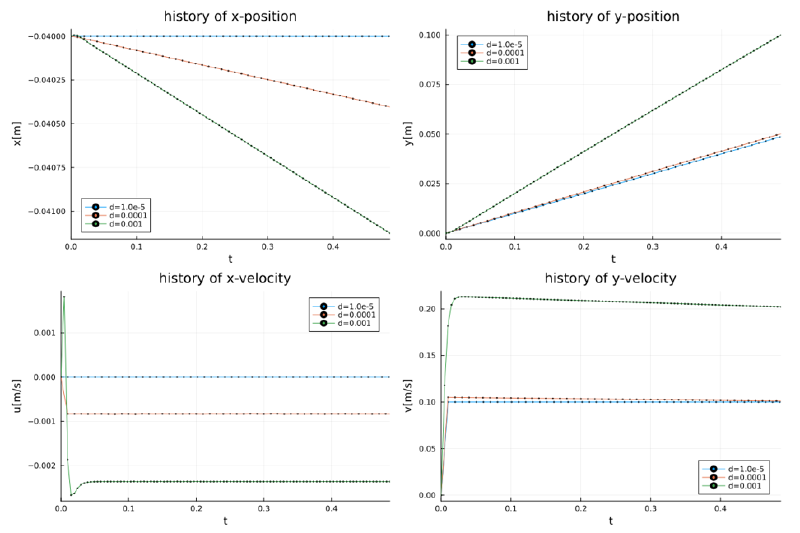
case-7
このケースはcase-6の流速方向を逆転したものであり、 相対速度と渦度のベクトル方向からサフマン力は$+x$方向となる。 この場合も粒径が大きいほうがサフマン力が顕著である。
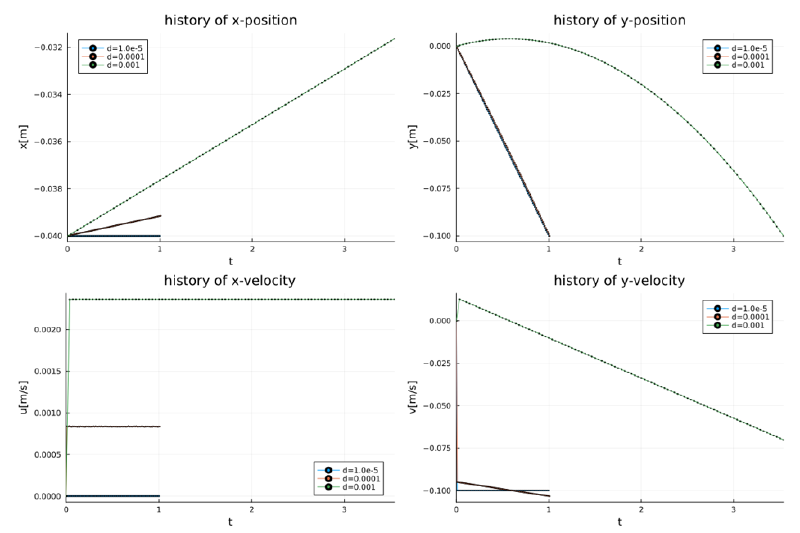
case-8
このケースは水滴粒子が空気中を落下するものである。粒径が1e-3と大きい。 重力項(浮力項)は長さの3乗に比例するのに対してサフマン項は長さの2乗に比例するため粒径が大きい場合には、 サフマン力の影響は相対的に小さくなっており、 粒子はほぼ自由落下していることがわかる。
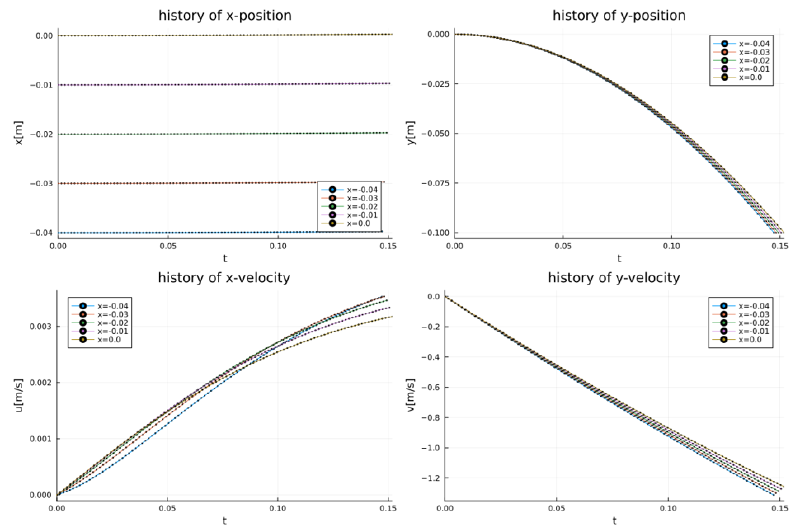
case-9
このケースはcase-8の粒径を1桁小さくしたものであり、 サフマン項の効果が顕著に見られる。 相対速度は上向き($+y$方向)、$\omega$は紙面上向き方向から$+x$方向のサフマン力が発生している揚力が発生していることがわかる。
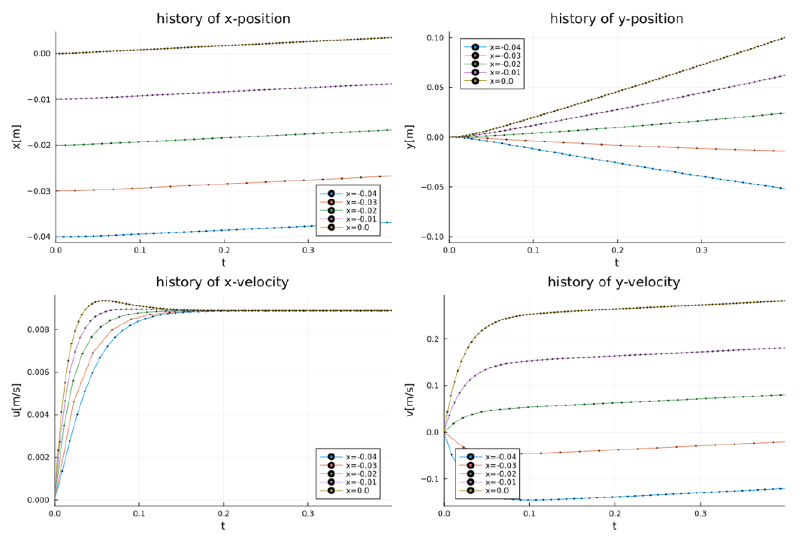
case-10
このケースはcase-9の粒径をさらに1桁小さくしたものであり、 粒子緩和時間が微小となるためサフマン力はほぼゼロとなっている。
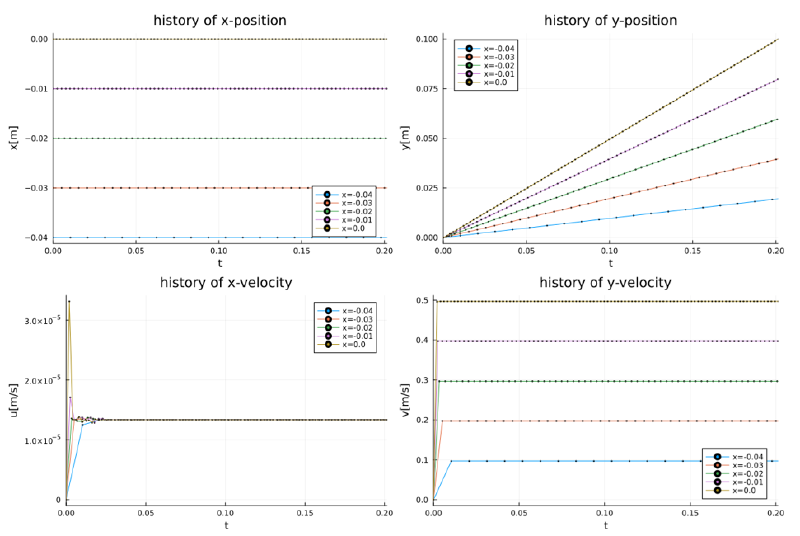
case-11
このケースは下向き流速の場を水滴粒子が落下する場合となっており、サフマン項の影響は見られない。
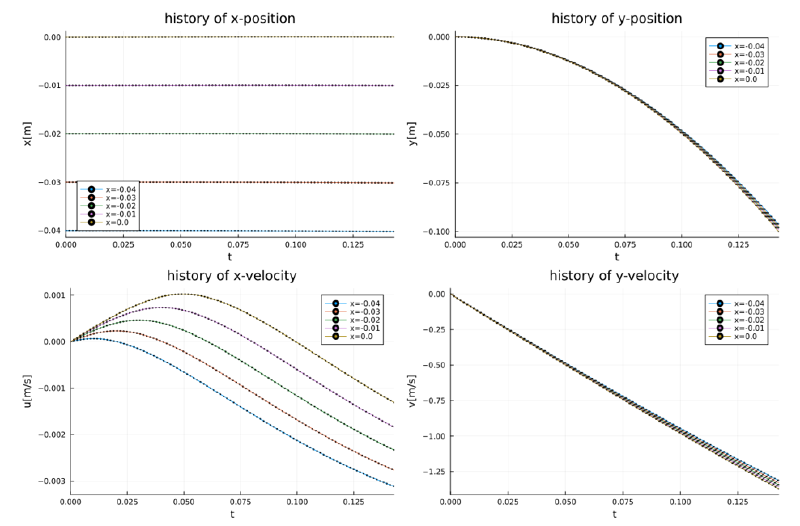
case-12
このケースもcase-11と同様である。
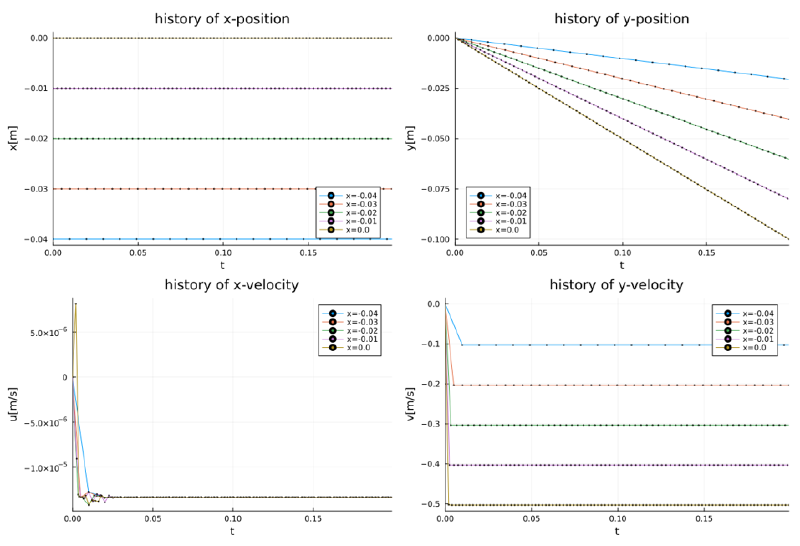
case-13
このケースは粒径の効果を見たものであり、粒径が小さい場合は粒子は流体に追随、 粒径が大きくなるとサフマン力が顕著となっている。 サフマン力は$d=1e$-$4$の場合が最も大きくなっている。
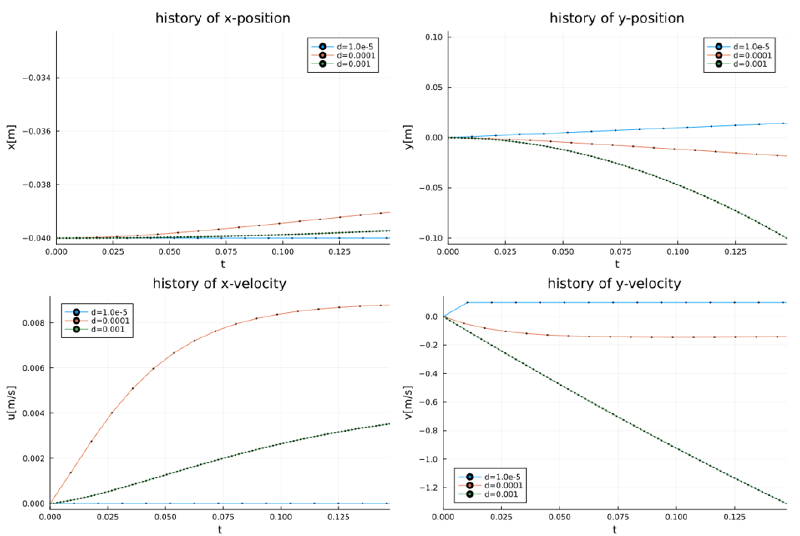
case-14
このケースはcase-13と同様に説明できる。
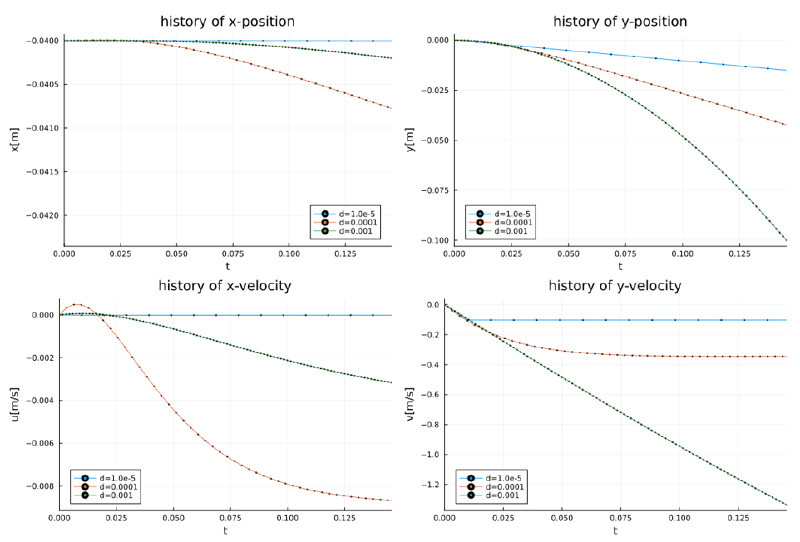
case-15
このケースは下向きの放物流速分布の場に気泡粒子を放出した場合である。 両端の気泡粒子は浮力の影響により上昇し、中央部では下降している。
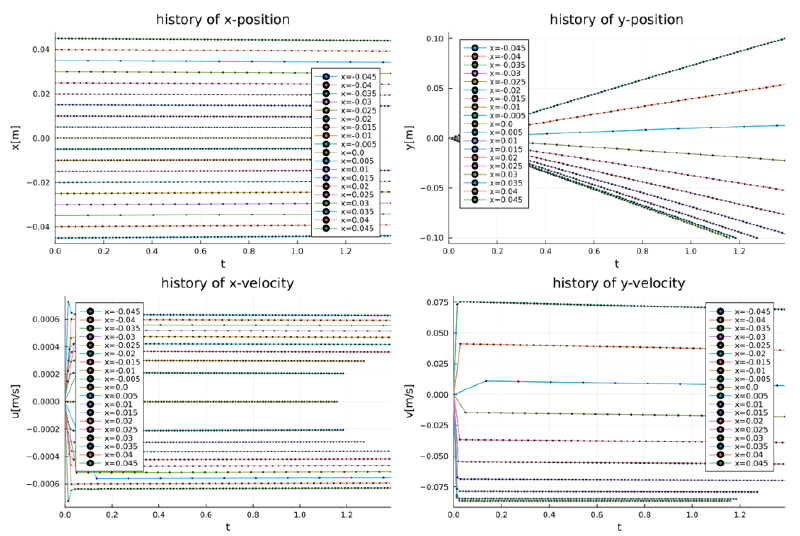
粒子追跡プログラム
以下に今回のシミュレーションで使用したjuliaプログラムを示す。 計算に必要なパラメータは全て paramete.jlの中で定義している。
#(parameter.jl)
# 流路形状
leng = 0.1 # 流路長さ
hb = 0.05 # 流路半幅
# 粒子=空気、流体=水
rhop = 1.2; rhof = 1000; muf = 1e-3
# 粒子=水、流体=空気
# rhop = 1000; rhof = 1.2; muf = 1.8e-5
# 粒子回転角速度(マグナス効果)
omgp = 0
# 粒径
dp = 1e-5
# 粒子放出位置
xini = -0.04
# 粒子放出速度
# (1) directly specify velocity value
vini = 0
# (2) set same value as velocity-profile
# vini = nothing
# 流速分布タイプ
type = "uniform"
# type = "linear"
# type = "parabolla"
# 最大流速
# vmax = 1.0
vmax = 0.0
# vmax = -1.0
#(eqn.jl)
using DifferentialEquations
using Plots
struct Geometry{T<:AbstractFloat}
length::T
hwidth::T
end
@kwdef struct Ufield{T<:AbstractFloat}
vmax::T
profile::Function
saffman::Function
end
#----------------------------------
function morsi_alexander(Re)
if Re < 0.1
CdRe = 24;
elseif Re < 1.0
CdRe = (3.690 + (22.73/Re) + (0.0903/(Re*Re)))*Re;
elseif Re < 10.0
CdRe = (1.222 + (29.1667/Re) + (-3.8889/(Re*Re)))*Re;
elseif Re < 100.0
CdRe = (0.6167 + (46.50/Re) + (-116.67/(Re*Re)))*Re;
elseif Re < 1000.0
CdRe = (0.3644 + (98.33/Re) + (-2778/(Re*Re)))*Re;
elseif Re < 5000.0
CdRe = (0.357 + (148.62/Re) + (-47500/(Re*Re)))*Re;
elseif Re < 10000.0
CdRe = (0.46 + (-490.546/Re) + (578700/(Re*Re)))*Re;
else
CdRe = (0.5191 + (-1662.5/Re) + (5416700/(Re*Re)))*Re;
end
return CdRe
end
#----------------------------------
function get_cl(dp,udif,omgp)
sp = (udif<eps() ? 0 : 0.5*dp*abs(omgp)/udif)
return 2*sp
end
#----------------------------------
function get_cs(dp,udif,rhof,muf)
re = 0.5*dp*udif*rhof/muf
cs = exp(-re/20.0)
return cs
end
#----------------------------------
function particle!(du,u,p,t)
dp, coefp, coeff, ratio, rhop, rhof, muf, omgp, gravity, ufluid = p
# u[1] --> x-coord
# u[2] --> x-velocity
# u[3] --> y-coord
# u[4] --> y-velocity
xp, up, yp, vp = u
uf, vf = ufluid.profile(xp, yp)
udif = sqrt((uf-up)^2 + (vf-vp)^2)
Re = rhof * dp * udif / muf
cdre = morsi_alexander(Re)
taup = rhop*dp^2/(18*muf) * 24/cdre
gravx, gravy = gravity()
cl = get_cl(dp,udif,omgp)
cs = get_cs(dp,udif,rhof,muf)
(saffx, saffy) = ufluid.saffman(xp,up, yp,vp, uf,vf)
(magnx, magny) = ( (vf-vp)*sign(omgp),
-(uf-up)*sign(omgp) )
du[1] = up
du[2] = (
(uf-up)/taup
+ 0.75*cl/dp*ratio*udif*magnx
+ 9.66*cs/(pi*dp)*sqrt(muf*rhof)/rhop*saffx
+ (1-ratio)*gravx
) / coefp
du[3] = vp
du[4] = (
(vf-vp)/taup
+ 0.75*cl/dp*ratio*udif*magny
+ 9.66*cs/(pi*dp)*sqrt(muf*rhof)/rhop*saffy
+ (1-ratio)*gravy
) / coefp
end
#----------------------------------
function track(params)
(cm,rhop,rhof,muf,dp,omgp,inipos,inivel,gravity,ufluid,geom) = params
hb = geom.hwidth
leng = geom.length
ratio = rhof/rhop
coefp = 1 + ratio*cm
coeff = ratio*(1 + cm)
(xini, yini) = inipos()
(xvel, yvel) = inivel(xini, yini)
u0 = [ xini, xvel, yini, yvel ]
tspan = (0.0, 1e4)
# when particle hit outlet face, terminate calculation
# also, particle will reflect when hitting side wall
function condition(out, u, t, integrator)
out[1] = leng-abs(u[3])
out[2] = (hb-u[1])*(hb+u[1])
end
function affect!(integrator, idx)
if idx == 1
terminate!(integrator)
elseif idx == 2
integrator.u[2] = -integrator.u[2]
end
end
cb = VectorContinuousCallback(condition, affect!, 2)
p = [ dp, coefp, coeff, ratio, rhop, rhof, muf, omgp, gravity, ufluid ]
prob = ODEProblem(particle!, u0, tspan, p)
sol = solve(prob, callback=cb )
(nrow,ncol) = size(sol)
lasttime = sol.t[ncol]
times = Vector{Float64}(undef,ncol)
xps = Vector{Float64}(undef,ncol)
ups = Vector{Float64}(undef,ncol)
yps = Vector{Float64}(undef,ncol)
vps = Vector{Float64}(undef,ncol)
for j=1:ncol
time = sol.t[j]
xp = sol.u[j][1]
up = sol.u[j][2]
yp = sol.u[j][3]
vp = sol.u[j][4]
times[j] = time
xps[j] = xp
ups[j] = up
yps[j] = yp
vps[j] = vp
end
out = open( "outfile", "w")
println(out,"time xps ups yps vps")
for j=1:ncol
println(out,times[j]," ",xps[j]," ",ups[j]," ",yps[j]," ",vps[j])
end
close(out)
# animation (trajectory)
nframes = 100
anim = @animate for t in LinRange(0, lasttime, nframes)
plt = plot(sol, idxs = (1,3), tspan = (0.0, t), label = false)
scatter!(sol, idxs = (1,3), tspan = (t, t), lab = nothing)
plot(plt, layout = (1,1),
xaxis = ("x" ,(-0.05, 0.01)),yaxis = ("y" ,(0, 0.1)),
plot_title = "t = $(round(t, digits = 2))")
end
gif(anim, "trajectory.gif"; fps = 10)
# trajectory plot
plot(sol,idxs=(1,3), title="trajectory",
markershape=:circle, markersize=1, plotdensity=100,
xlabel="x[m]", ylabel="y[m]", label=nothing )
savefig("trajectory.png")
# history plot
plot(sol,idxs=(0,1), title="history of x-position",
markershape=:circle, markersize=1, plotdensity=100,
xlabel="time[sec]", ylabel="x[m]", label="xp")
savefig("hist-xp.png")
plot(sol,idxs=(0,2), title="history of x-velocity",
markershape=:circle, markersize=1, plotdensity=100,
xlabel="time[sec]", ylabel="u[m/s]", label="up")
savefig("hist-up.png")
plot(sol,idxs=(0,3), title="history of y-position",
markershape=:circle, markersize=1, plotdensity=100,
xlabel="time[sec]", ylabel="y[m]", label="yp")
savefig("hist-yp.png")
plot(sol,idxs=(0,4), title="history of y-velocity",
markershape=:circle, markersize=1, plotdensity=100,
xlabel="time[sec]", ylabel="v[m/s]", label="vp")
savefig("hist-vp.png")
end
#----------------------------------
function run()
# all simulation parameters are imported from parameter.jl
include("parameter.jl")
if @isdefined xinis
yinis = fill(0.0, length(xinis))
inipos = () -> ( xinis, yinis )
else
inipos = () -> ( xini, 0.0 )
end
if vini == nothing
inivel = (xp,yp) -> ( ufluid.profile(xp,yp) )
else
inivel = (xp,yp) -> ( 0.0, vini )
end
cm = 0.5 # virtual mass coef. for sphere
geom = Geometry( leng, hb )
gravity = () -> ( 0.0, -9.81 )
if type == "uniform"
ufluid = Ufield(
vmax = vmax,
profile = (xp,yp) -> (0.0, vmax),
saffman = (xp,up, yp,vp, uf,vf) -> (0,0),
)
elseif type == "linear"
ufluid = Ufield(
vmax = vmax,
profile = (xp,yp) -> (0.0, vmax/(2*hb)*(xp+hb)),
saffman = (xp,up, yp,vp, uf,vf) -> begin
omega = 0.5*vmax/hb
bunbo = sqrt(abs(omega))
return ( (vf-vp)*omega,
-(uf-up)*omega )
end
)
elseif type == "parabolla"
ufluid = Ufield(
vmax = vmax,
profile = (xp,yp) -> (0.0, vmax*(1.0 - (xp/hb)^2) ),
saffman = (xp,up, yp,vp, uf,vf) -> begin
bunbo = sqrt(2*abs(vmax*xp))/hb
if bunbo < eps()
return ( 0.0, 0.0 )
else
return ( -2*vmax*(vf-vp)*xp/hb^2 /bunbo,
2*vmax*(uf-up)*xp/hb^2 /bunbo )
end
end
)
end
params = (cm,rhop,rhof,muf,dp,omgp,inipos,inivel,gravity,ufluid,geom)
track(params)
end
run()
まとめ
流体中における粒子の運動を追跡するシミュレータを作成した。
サフマン揚力の効果に注目し、いくつかのテスト計算を実施した。
サフマン揚力は、以下の特徴を持つことがわかった。
- 粒径が極めて小さい場合、粒子緩和時間が極めて小さくなり、 その結果、粒子は流体に追随して移動する。両者の速度差がほぼゼロとなりサフマン揚力はほぼゼロとなる
- 粒径が極めて大きい場合、長さの$3$乗に比例する体積力項が、長さの$2$乗に比例する面積力項よりも支配的となる。 浮力項は前者、サフマン項は後者であり、その結果サフマン揚力の影響は顕著ではなくなる
- 式を見れば明白であるが、サフマン揚力の作用する方向は相対速度$(\mathbf{u}-\mathbf{v})$と渦度$\omega$の外積の方向で決まる
弊社の解析事例
弊社の流体解析事例については、下記のリンクからご覧ください.