テイラー渦流れ
By Y.Sasaki
はじめに
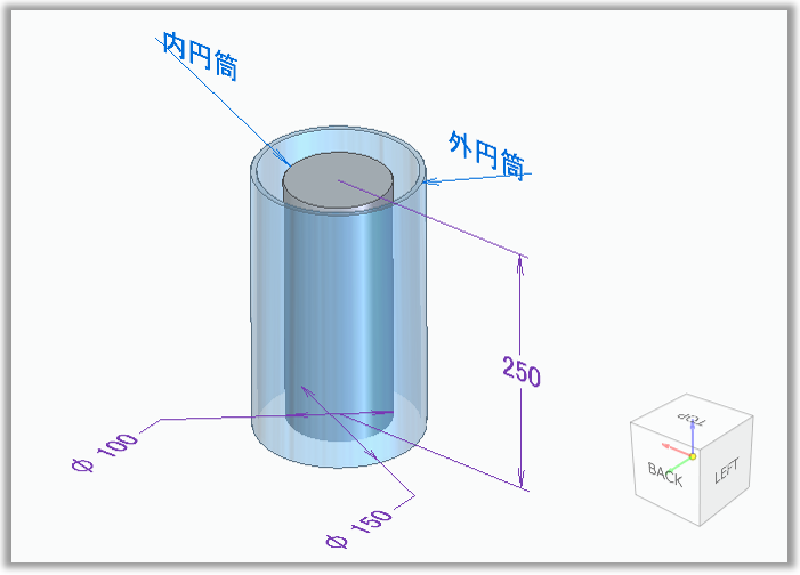
半径の差が直径に比較して小さい二つの同心円筒の内部が流体で満たされ、 外側の円筒は静止した状態で内円筒を回転させるとドーナツ状のたがいに反対方向に回転する渦の列が形成され、 これをテイラー渦と呼んでいます。
二つの円筒がともに回転している場合も、回転角速度が妥当な条件であればテイラー渦が形成されます。
このテイラー渦は、流体塊に働く遠心力とその周囲の圧力が釣合わない(遠心力不安定)ために生じるものです。
テイラー渦流れは、外乱に対して強い安定性を持ち、攪拌装置、ジャーナル軸受などの様々な流体機械に用いられています。
テイラー数 (Ta)
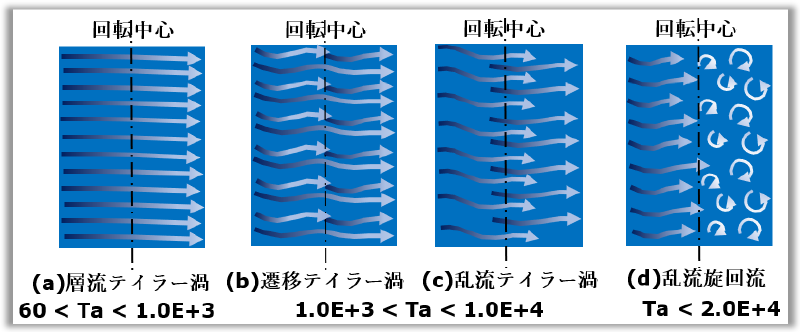
この回転二重円筒間の流れは、回転数の増加に伴いセルと呼ばれるトーラス状の流れが幾重にも重なって現われ
- (a) 層流テイラー渦
- (b) 遷移テイラー渦
- (c) 乱流テイラー渦
- (d) 乱流旋回流
へと遷移して行きます。
この回転粘性流で出現する無次元量テイラー数(Ta)は以下のように表されます。
$$ Ta \equiv Re \left( \frac{d}{Ri} \right)^{\frac{3}{2}} $$
ここで、
$$ Re \equiv \frac{Ui\cdot Ri}{v} = \frac{Ri^2 \cdot \Omega i}{v} $$
- 内筒半径(m) : $Ri$
- 内筒周速(m/s) : $Ui$
- 外筒半径(m) : $Ro$
- 内筒角速度(rad/s) : $\Omega_i$
- 半径比 : $Ri/Ro$
- 円筒と外筒の半径方向すきま(m) : d
- すきま比 : $d/Ri$
計算例
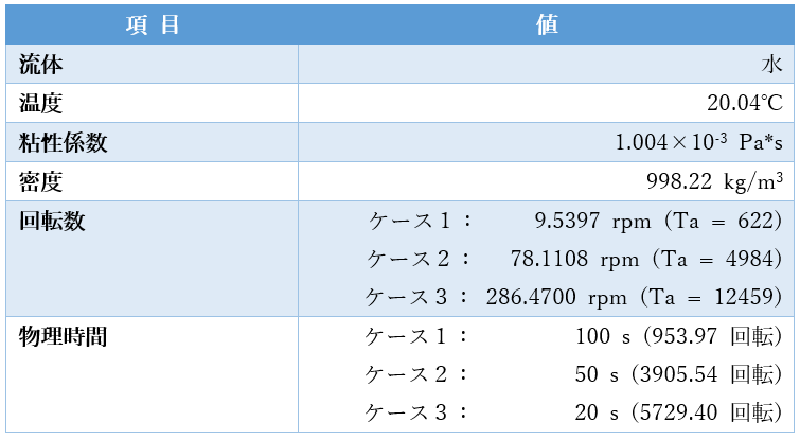
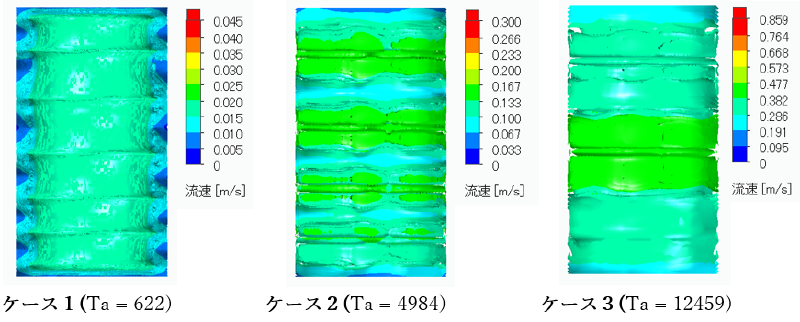
次の3つのテイラー数について計算を行い、それぞれの流れの違いを確認しました。
比較したケースは
- Ta = 622の層流テイラー渦流れ
- Ta = 4984の遷移テイラー渦流れ
- Ta = 12459の乱流旋回流れ
の3つです。
計算結果
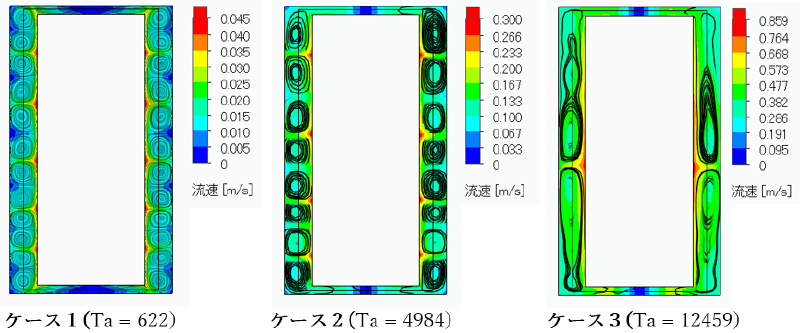
ケース1では、径方向中心断面の流速分布から6組の対になる安定した層流テイラー渦が形成され、蛇行もなく安定した流れであることが等値面図から分かります。
ケース2では、渦に歪みが生じ遷移テイラー渦に移行しており、4組の対の渦が形成されています。また等値面図からも流れ振動している様子が分かります。
ケース3では、テイラー渦は消失し始め乱流テイラー渦に移行していることが径方向中心断面の流速分布及び等値面図から確認出来ます。
弊社の解析事例
弊社の流体解析事例については、下記のリンクからご覧ください.