時空間変動する流入境界条件の開発
By M.Sato
概要
任意の断面形状の流路に対して時間変動する流入境界条件を設定することを考える。
流路断面に流速分布形状を指定する必要があるが、最も単純な指定は一定値である。 流れのレイノルズ数が十分大きければこのような一様分布で近似しても問題はない。 もしレイノルズ数が小さく流れが層流であれば流速分布はポテンシャル流れに類似したものになるはずである。
OpenFOAMには時間変動するポテンシャル流れの流速分布形状を簡単に指定する方法が無かったため、このようなタイプの境界条件を作成した。
💡 本境界条件の特徴
- 空間分布パターンと時間変動パターンを分離して指定可能
- ポテンシャル流れなど任意の流速分布形状に対応
- 血流解析など脈動流の境界条件設定に最適
テスト計算により正しく動作することが確認できた。 この境界条件タイプを使うことにより例えば大動脈を通過する脈動流の境界条件を適切に指定することができる。
開発の動機
前回のブログにおいてwindkessel境界について紹介した。
そこで実際の血管に対して、このモデルを適用してみたい。 OpenFOAMでは、時間変動する流速境界条件を指定することができる。
例えば以下に示すような指定が可能である。
ℹ️ OpenFOAMの既存境界条件タイプ
✅ codedFixedValueタイプ境界
- 境界条件ファイルの中に自分でc++でコードを記述
- 任意の流速分布を指定可能である
- 必要に応じて流速の空間分布、時間変化データをファイルなどから読み込む
✅ uniformValueFixedタイプ境界
- 空間分布については一様値
- 時間パターンについては Function1関数オブジェクトを使い任意の関数形を指定可能
✅ timeVaryingMappedFixedValueタイプ境界
- 実験データなどを指定するのに便利
- 時間変動は時刻ごとのデータをファイルとして用意する必要がある
今回は大動脈を通過する血流の解析を行いたいので、上記の指定方法が使えないか考えてみる。
⚠️ 既存境界条件の課題
❌ codedFixedValueではc++のコーディングが難しそうである(ファイル読み込み管理、座標の対応関係など)
❌ uniformValueFixedでは空間的な分布を与えることができない
❌ timeVaryingMappedFixedValueでは各時刻の流入速度データを用意すれば、使用できるが時間パターンが長期間にわたる場合には使いづらい
流速の空間分布と時間変動パターンを組み合わせて指定することで簡易的に境界条件を指定したいが これらの境界条件タイプでは難しそうである。
💡 ということで、もっと扱いやすい境界条件タイプを自作することにした。
境界条件の指定方針
血流は脈動しており、非常に高速の流れになっているわけではない(Re数が十分発達した乱流状態にはなっていないという意味)。
従って流入部の流速空間分布はポテンシャル流れで近似できると仮定する。 これには低Re数流れの解を使用することができる。
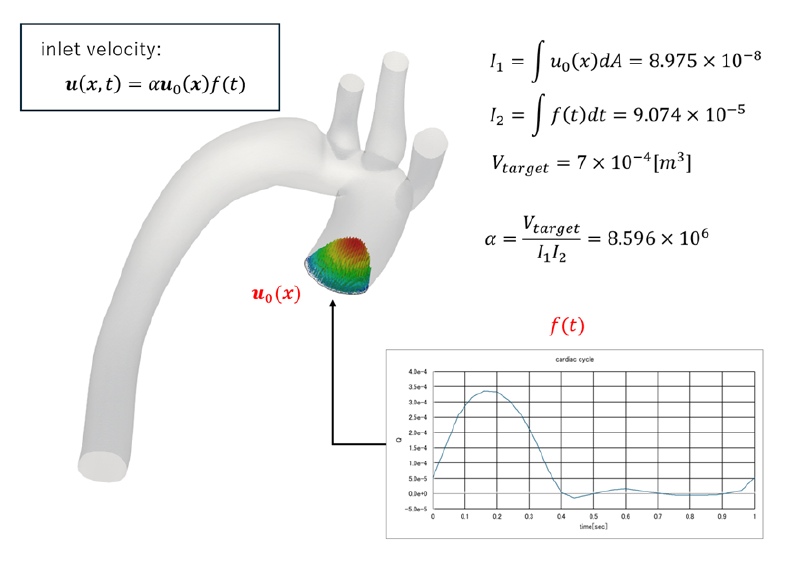
血液は脈動しているがこれは流量の経時変化から時間変動パターンを知ることができる。 流入境界の流速$\mathbf{u}(\mathbf{x},t)$は次式で表されると仮定する。
$$ \begin{align} \mathbf{u}(\mathbf{x},t) &= \alpha \times \mathbf{u}_0(\mathbf{x})\times f(t) \notag \end{align} $$
📝 記号の説明
- $\mathbf{x}$:位置ベクトル
- $t$:時間
- $\alpha$:値を調整するための係数
- $\mathbf{u}_0(\mathbf{x})$:流入速度の空間分布パターン
- $f(t)$:時間変動パターン
$\mathbf{u}_0(\mathbf{x})$および$f(t)$は、あくまでパターン値なので現実値に変換するために調整係数$\alpha$を掛けるようにしている。
心臓の1拍動当たりの拍出量$V[m^3]$は流速分布から次式で表される。
$$ \begin{align} V &= \int_A \int_t \mathbf{u}(\mathbf{x},t) dA dt \notag \\ & = \int_A \int_t \alpha \mathbf{u}_0(\mathbf{x})f(t) dA dt \notag \\ & = \alpha \int_A \mathbf{u}_0(\mathbf{x})dA \int_0^T f(t) dt \notag \end{align} $$
ここで$T$は心拍の1周期時間である。$\mathbf{u}_0(\mathbf{x})$および$f(t)$が既知であれば、これから$\alpha$を求めることができる。
$$ \begin{align} \alpha &= \frac{V}{\int_A \mathbf{u}_0(\mathbf{x})dA \int_0^T f(t) dt } \notag \end{align} $$
❤️ 成人の心拍出量
成人の場合、1拍動当たりの拍出量は $V=70 [mL]$ 程度であると言われている。
境界条件の実装
OpenFOAMに標準で組み込まれているtimeVaryingMappedFixedValueタイプ境界が類似した境界条件になっているので これをベースにして新しい境界条件(spaceTimeVaryingMappedFixedValue)を作成した。
⭐ 新規境界条件: spaceTimeVaryingMappedFixedValue
既存の
timeVaryingMappedFixedValueをベースに、空間分布パターンと時間パターンを独立して指定できるように拡張
以下に実装の要点を記述する。
1️⃣ 空間分布、時間パターンを保持する変数を定義
ファイル: spaceTimeVaryingMappedFixedValue.H
autoPtr<PatchFunction1Types::MappedFile<Type>> spacePattern_;
autoPtr<Function1<scalar>> timePattern_;
scalar scaling_;
📝 実装のポイント
timePattern_はFunction1タイプの変数としている。spacePattern_は元々のuniformValue_と同じ内容であるが変数名を変更した。
2️⃣ 変数の初期化
ファイル: spaceTimeVaryingMappedFixedValue.C
spaceTimeVaryingMappedFixedValueFvPatchField
(
const fvPatch& p,
const DimensionedField<Type, volMesh>& iF,
const dictionary& dict
)
:
fixedValueFvPatchField<Type>(p, iF, dict, IOobjectOption::NO_READ),
spacePattern_
(
new PatchFunction1Types::MappedFile<Type>
(
p.patch(),
"spacePattern",
dict,
iF.name(), // field table name
true // face values
)
),
timePattern_
(
Function1<scalar>::New("timePattern", dict)
),
scaling_(dict.getOrDefault<scalar>("scaling", 1.0))
{
if (!this->readValueEntry(dict))
{
// Note: we use evaluate() here to trigger updateCoeffs followed
// by re-setting of fvatchfield::updated_ flag. This is
// so if first use is in the next time step it retriggers
// a new update.
this->evaluate(Pstream::commsTypes::buffered);
}
}
📄 空間分布の処理
空間分布はMappedFile関数で計算している。この関数は複数の時刻データがある場合には中間の時刻での値を線形補間するようになっている。
今回の境界条件ではこのような余計な処理は不要なので、
constant/boundaryDataでは必ず時刻0の値(流速分布)のみを指定する。
3️⃣ 境界条件の計算
ファイル: spaceTimeVaryingMappedFixedValue.C
void Foam::spaceTimeVaryingMappedFixedValueFvPatchField<Type>::updateCoeffs()
{
if (this->updated())
{
return;
}
const scalar t = this->db().time().value();
fvPatchField<Type>::operator==(spacePattern_->value(t)
*timePattern_->value(t)
*scaling_);
fixedValueFvPatchField<Type>::updateCoeffs();
}
⚙️ 計算方法
空間パターン、時間パターン、調整係数を掛けて境界条件値を計算している。
解析例
💻 解析モデル
実際の血管を対象とするため、オープンソースの血管形状データベースから適当な大動脈形状をダウンロードした。
モデル形状を以下に示す。
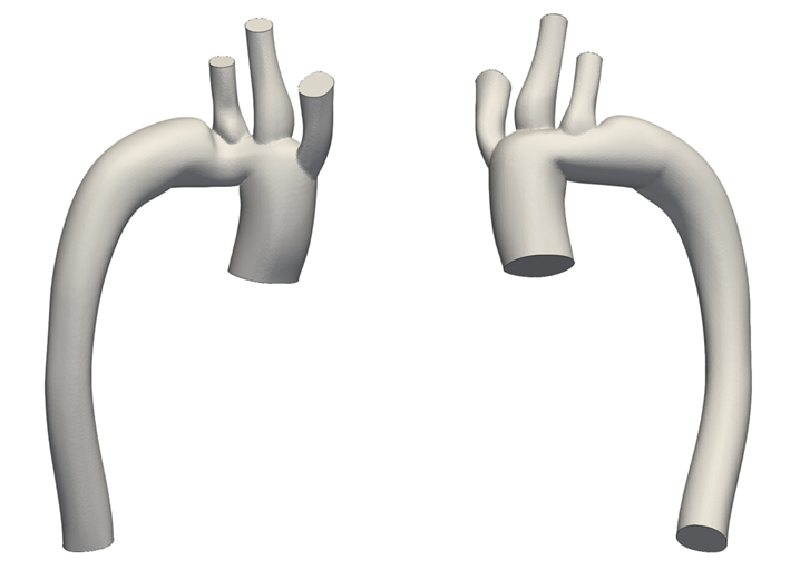
ℹ️ モデル形状
実際の大動脈形状を使用した血流解析モデル
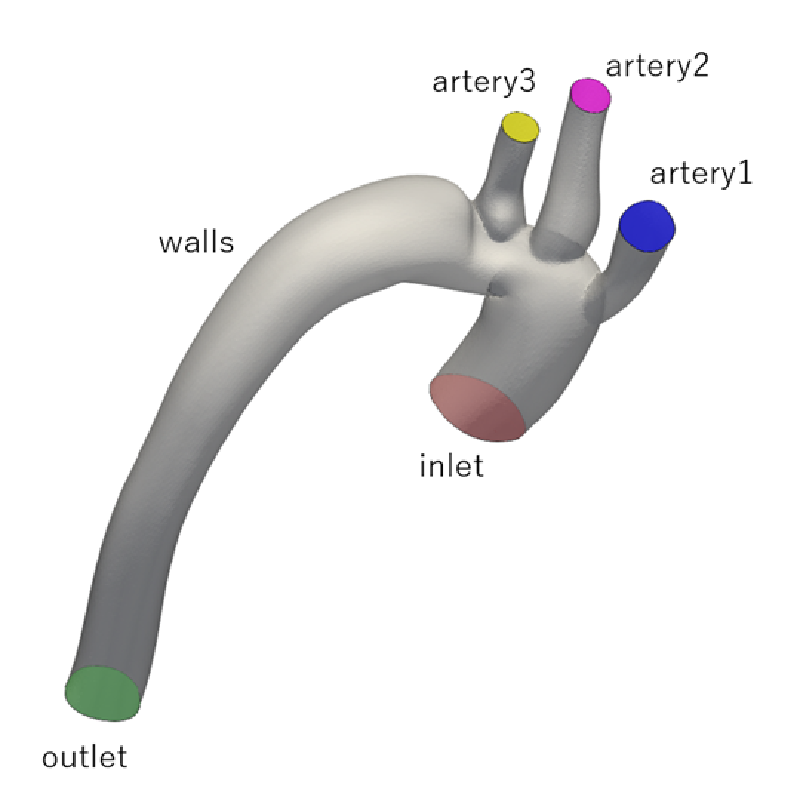
✂️ 境界パッチの分割
元の形状(STLファイル)は全面が単一の境界面になっていたため、流出入面を区別できるように境界面を分割した。
💡 境界面分割の方法
推奨: foundation版のOpenFOAM(OpenFOAM-13)では
surfaceAutoPatchコマンドが利用できるのでこれを使うのが最も簡単である。代替案: paraviewで分割を行いたい場合は、STLファイル読み込み後、以下の手順でフィルターを操作すれば境界面の分割が可能である。
"Generate Surface Normal" -> "connectivity" -> "threshould"で番号 指定 -> "extract surface"の後でファイル保存
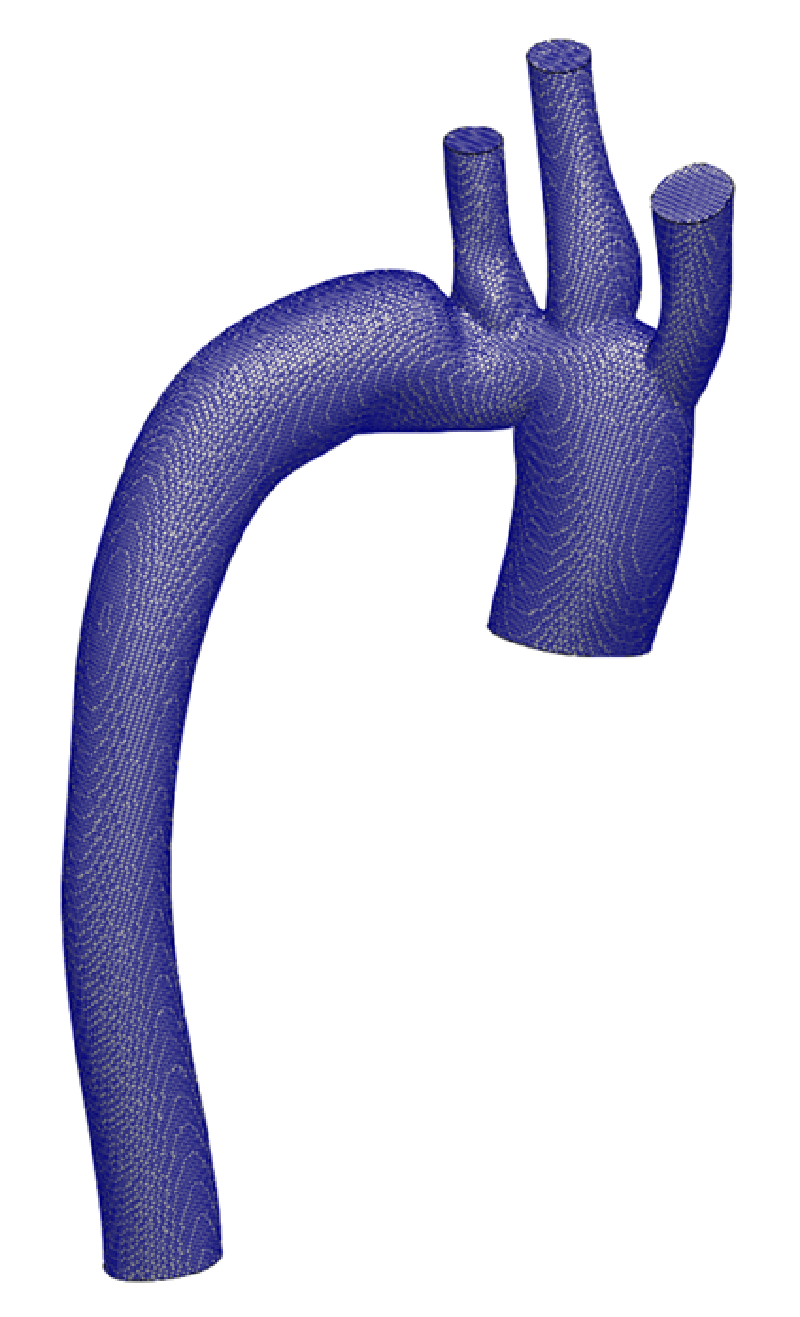
📐 メッシュ分割
OpenFOAMに付属のメッシャsnappyHexMeshを使いメッシュを作成した。
以下にメッシュ分割図を示す。
💧 物性値
ℹ️ 流体物性値(血液)
物性 値 単位 密度 $\rho$ 1060 kg/m³ 粘度 $\mu$ 0.004 Pa·s
🔄 解析手順
解析は二段階に分けて実施した。
📖 解析フロー
STEP 1: 流入速度空間分布を求めるための定常解析
- 流入圧力指定
- 低Re数流れ
STEP 2: 時空間変動流入速度を指定した非定常解析(本番計算)
📈 流入流速の空間パターン
定常解析で得られた結果に基づき、関数オブジェクトを使い流入流速分布データおよび流入境界での体積流量を求める。
以下に関数オブジェクト計算の指定を示す。
設定ファイル: system/controlDict 内の functions
functions
{
sample.inlet
{
type surfaces;
libs (sampling);
writeControl writeTime;
surfaceFormat foam;
interpolationScheme face;
fields (U);
surfaces
(
inlet
{
type patch;
patches ( "inlet" );
}
);
}
flowRateInlet
{
type surfaceFieldValue;
libs (fieldFunctionObjects);
enabled true;
writeControl timeStep;
writeInterval 1;
log true;
valueOutput true;
writeFields no;
regionType patch;
name inlet;
operation sum;
fields (phi);
}
};
⚠️ データのコピー
流速分布データは
postProcessing/sample.inlet/(ステップNo)/inletに保存されているので、これらを非定常解析の境界データとしてコピーする。cp (定常解析ケース)/postProcessing/sample.inlet/(ステップNo)/inlet/faceCenters \ (非定常解析ケース)/constant/boundaryData/inlet/points cp (定常解析ケース)/postProcessing/sample.inlet/(ステップNo)/inlet/vectorField/U \ (非定常解析ケース)/constant/boundaryData/inlet/0/U
👉 flowRateInletで計算された流量値は調整係数$\alpha$を求めるために使われる。
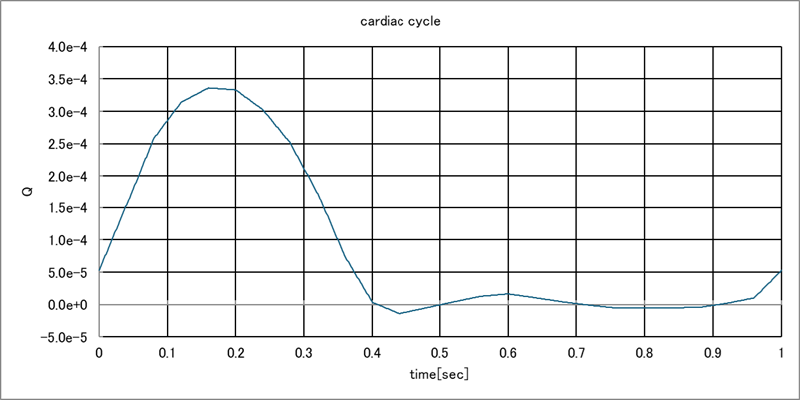
💓 流量の時間パターン
ここでは、以下の資料の例を使用した。
時間パターンデータを以下のファイル名で保存しておく。
データファイル: (非定常解析ケース)/constant/timeData/pulse.dat
(
( 0.00000 5.25792000E-05 )
( 0.00100 5.51130000E-05 )
. . .
. . .
( 0.99900 5.15172200E-05 )
( 1.00000 5.25792000E-05 )
);
⚙️ 境界条件(非定常解析)
非定常解析では、流入境界(inlet)には今回作成した spaceTimeVaryingMappedFixedValueタイプを指定した。
✅ 境界条件設定のポイント
- 流入速度分布および流量の時間変動パターンを組み合わせて指定
- 一拍動当たりの流量が70[mL]と仮定
- 調整係数 $\alpha=8.596\times10^6$ と設定
- 流出境界:圧力ゼロ(本来ならばwindkesselモデルを指定)
- 壁面:速度ゼロ
設定ファイル: 0/U の抜粋
inlet
{
type spaceTimeVaryingMappedFixedValue;
mapMethod nearest;
scaling 8.596e6; // = 7e-5 / (8.974624582e-08 * 9.0738e-5)
timePattern tableFile;
timePatternCoeffs
{
file "$FOAM_CASE/constant/timeData/pulse.dat";
interpolationScheme linear;
outOfBounds repeat;
}
}
📊 解析結果
ℹ️ 解析条件
項目 設定値 ソルバー pimpleFOAM 時間刻み 可変 解析期間 2秒間(2拍動分) 可視化期間 時刻1~2秒
以下にいくつかの計算結果のアニメを示す(時刻1~2秒の間をアニメにしている)。
流入速度ベクトルを見ると正しく境界条件の設定が反映されていることがわかった。
流出入境界における流速ベクトル
血管内部における流速ベクトル
血管表面のオイルフロー流線(Line Integral Convolution)
🏥 実際の血管への適用
前述の計算結果は、流出境界(outlet, artery1~3) において圧力ゼロとし自由流出境界になっている。
これらの流出境界においてwindkessel境界を設定して計算を行ってみた。
⚠️ 計算上の制約
windkesselパラメータは文献などから適当な値を設定した。
その結果、計算の安定のために時間刻みを $10^{-6}[sec]$ 程度にする必要があり、筆者のノートPCでは計算時間がかかりすぎるため、実施できなかった。
❗ 重要な注意事項
前回のブログで紹介したwindkesselモデルでは境界における圧力の微分方程式の時間積分は固定時間刻みを仮定しているため、ソルバーの時間積分アルゴリズムはPISO法(pimpleFoamで
nOuterCorrectors=1)を使う必要があることに注意。
📝 まとめ
血流解析を行う際に流入速度の空間分布パターン、時間変動パターンを簡便に指定できるように新しくカスタム境界条件を作成した。
テスト計算の結果正しく動作していることがわかった。
🌟 開発成果
✅ 空間分布と時間パターンを独立して指定可能な境界条件を実装
✅ 大動脈モデルでの検証により正常動作を確認
✅ 脈動流の境界条件設定が簡便に
今回の解析で使用したデータは以下からダウンロード可能である。
⬇️ ダウンロード
🏢 弊社の解析事例
弊社の流体解析事例については、下記のリンクからご覧ください.