Windkesselモデルを用いた血流解析
By M.Sato
概要
Windkesselモデルは、血流の動態を簡略化して表現するための数学モデルで、例えば大動脈の圧力と流量の関係を記述するために使われる。
Windkesselはドイツ語で「風船(空気室)」を意味し、弾性容器としての動脈の性質をモデル化している。
以下にウィキペディアウィンドケッセルモデルに描かれている模式図を示す。
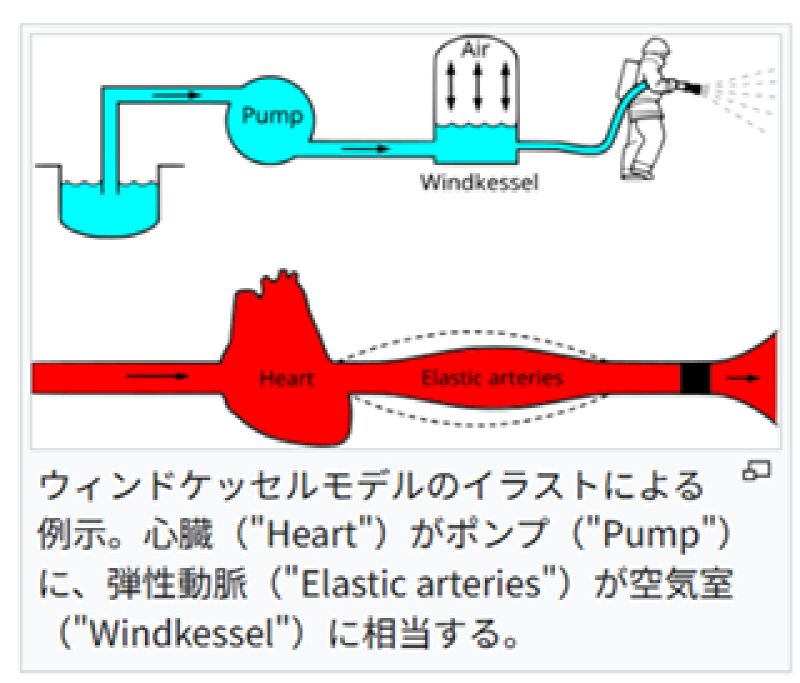
Windkesselモデルはシンプルな構造ながら、血行動態の理解に有用なツールであり、 数値シミュレーションや非侵襲的測定の解析にも広く利用されている。
例えば下図に示すような大動脈の解析では、 一部の血管を抽出して解析を行うことが必要であり、 流出側の切断面には弾性血管壁の貯留効果、 下流側の毛細血管の流動抵抗などを考慮することが適正なモデル化のために必須である。
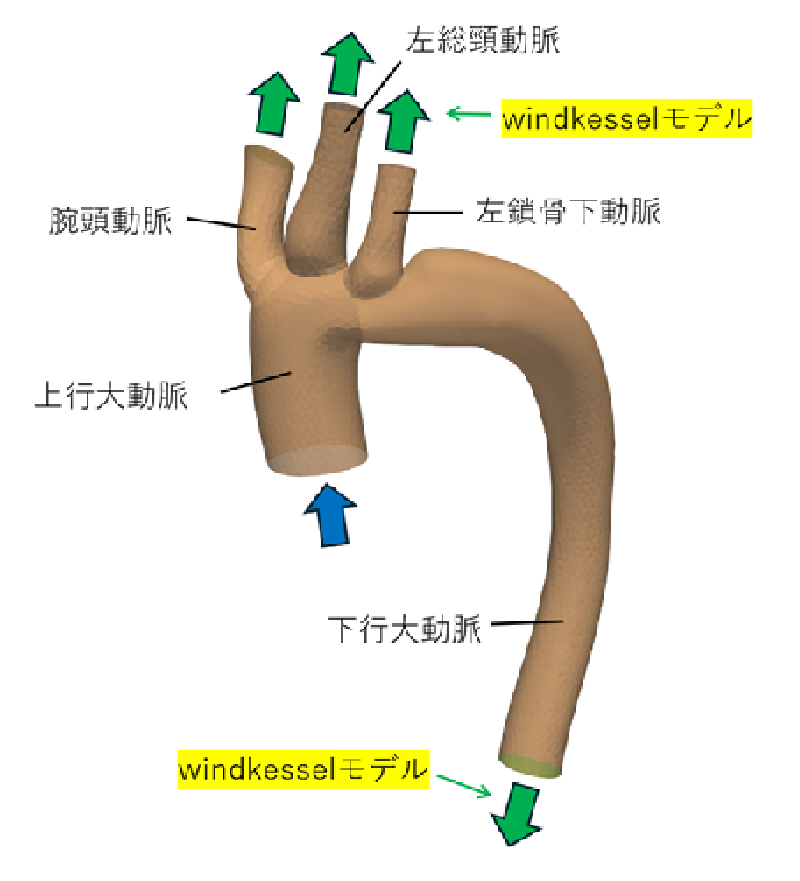
ここでは、OpenFOAMにWindkesselモデルを実装して計算した例を示す。
なお、OpenFOAMには先行研究でいくつかの実装例がある。
ここで参考にした資料は Implementation of Lumped Parameter Network Boundary Conditions for the Patient-Specific CFD Simulations of Coronary Arteries in OpenFOAM である。
Windkesselモデル
元々のwindkesselモデルは Otto Frank氏が最初に提案したものであり、 大きな血管のコンプライアンス(血液貯留効果)と毛細血管の抵抗を表現したモデルになっている。
その後、いくつかの改良モデルが提案されており、血管の近位(proximal)抵抗、 遠位(distal)抵抗、血液の慣性などを考慮することでより正確な表現が可能となった。
しかし精度のよい結果を得るためには、 これらのモデル要素のパラメータを測定して適切に同定することが必要である。 またwindkesselモデルは集中定数モデルであることから 境界条件適用箇所より先の部分の詳細な現象を 必ずしも正確に表現できていないことに注意しなければならない。
windkesselモデルは電流回路とのアナロジーで表現することができる。以下に対応関係を 示す。
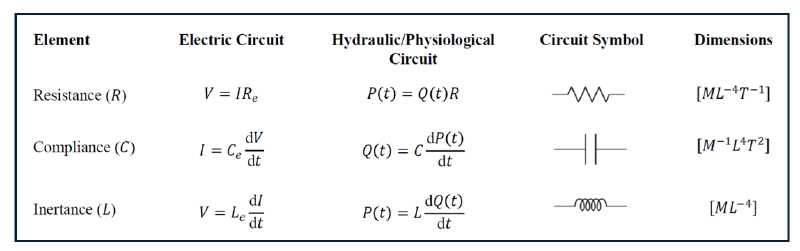
以下にいくつかの代表的なwindkesseuモデルを記述する。
2要素モデル
これは最も簡単なWindkesselモデルであり、下図に示すように遠位抵抗$R_d$、 キャパシタンス$C$、遠位圧力$P_d$で表される。
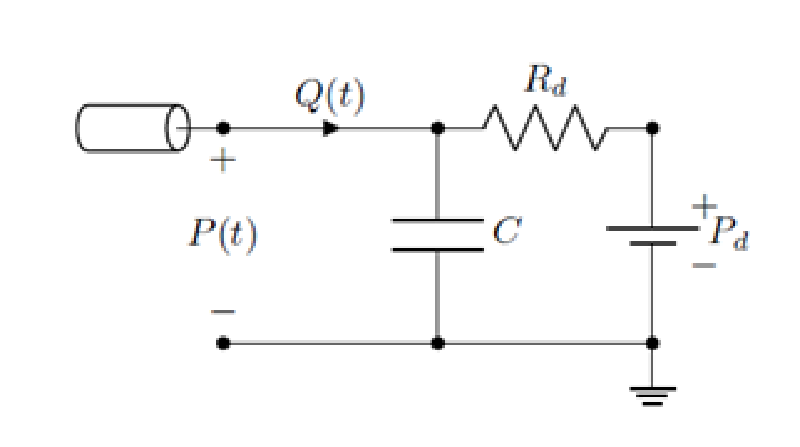
流量$Q(t)$と出口圧力$P(t)$の関係は次式で表される。
$$ \begin{align} Q(t) = C \frac{d P(t)}{dt} + \frac{ P(t)-P_d}{R_d} \end{align} $$
$$ \begin{align} P(t) = R_d Q(t) + P_d - R_d C \frac{d P(t)}{dt} \end{align} $$
3要素モデル
これは2要素モデルを改良したものであり、遠位抵抗$R_d$、 キャパシタンス$C$、遠位圧力$P_d$に、近位抵抗$R_p$を加えたモデルになっている。
このモデルは大動脈の特性インピーダンスを模擬することができる。
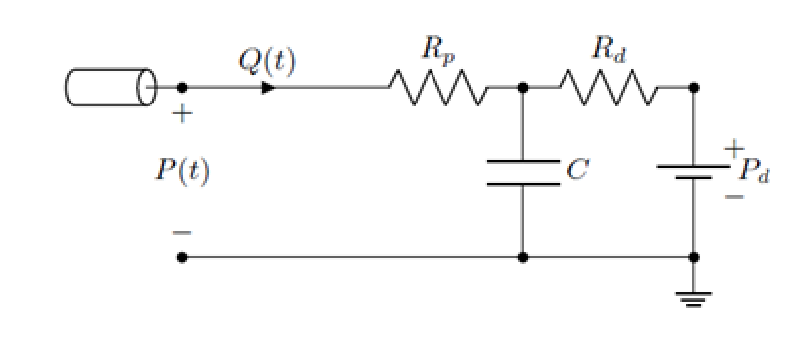
流量$Q(t)$と出口圧力$P(t)$の関係は次式で表される。
$$ \begin{align} \left( 1+ \frac{R_p}{R_d} \right) Q(t) +R_p C \frac{d Q(t)}{dt} = C \frac{d P(t)}{dt} + \frac{ P(t)-P_d}{R_d} \end{align} $$
$$ \begin{align} P(t) = R_p R_d C \frac{d Q(t)}{dt} + (R_p+R_d) Q(t)+P_d - R_d C \frac{d P(t)}{dt} \end{align} $$
4要素モデル(直列タイプ)
4要素モデルは回路内にインダクター(L)を含み、血流の慣性を考慮することができる。
4要素モデルは、2要素および3要素モデルと比較して、 血圧対心拍周期曲線をより正確に表現する。
インダクター$L$と近位抵抗$R_p$を直列に配置したモデルを下図に示す。
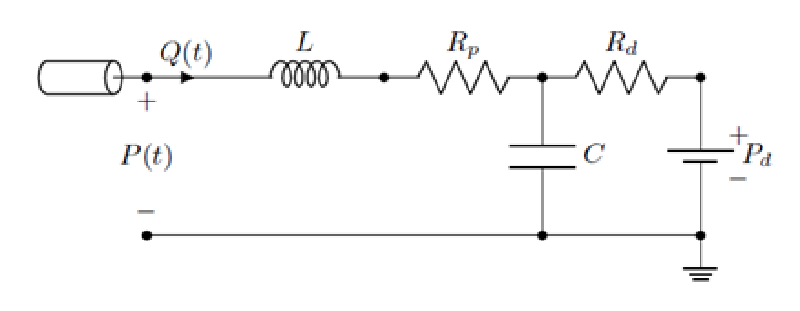
流量$Q(t)$と出口圧力$P(t)$の関係は次式で表される。
$$ \begin{align} \left( 1+\frac{R_p}{R_d} \right) Q(t) +\left( \frac{L}{R_d} + R_p C \right) \frac{d Q(t)}{dt} + CL \frac{d^2 Q(t)}{dt^2} = C \frac{d P(t)}{dt} + \frac{ P(t)-P_d}{R_d} \end{align} $$
$$ \begin{align} P(t) = (R_p+R_d) Q(t) + \left( L+R_p R_d C \right) \frac{d Q(t)}{dt} + R_d C L \frac{ d^2 Q(t)}{dt^2} +P_d - R_d C \frac{d P(t)}{dt} \end{align} $$
4要素モデル(並列タイプ)
4要素windkesselモデルにおいてインダクター$L$と近位抵抗$R_p$を並列に配置したモデルを下図に示す。
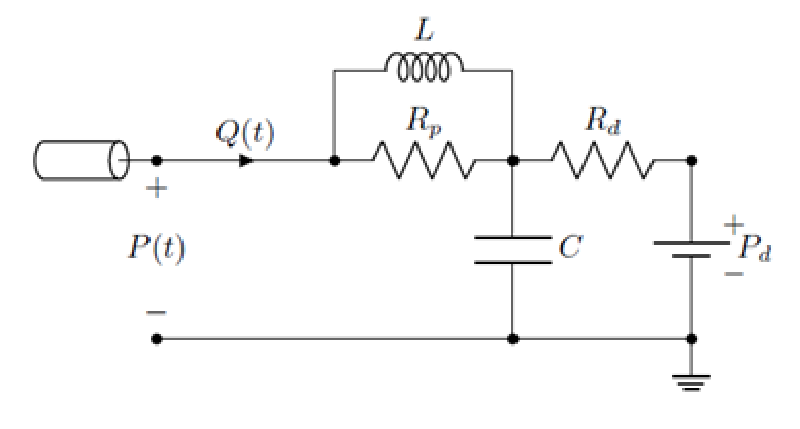
流量$Q(t)$と出口圧力$P(t)$の関係は次式で表される。
$$ \begin{align} Q(t) +L\left( \frac{R_p+R_d}{R_p R_d} \right) \frac{d Q(t)}{dt} + CL \frac{d^2 Q(t)}{dt^2} = \frac{CL}{R_p} \frac{d^2 P(t)}{dt^2} +\left( C + \frac{L}{R_p R_d} \right) \frac{d P(t)}{dt} +\frac{ P(t)-P_d}{R_d} \end{align} $$
$$ \begin{align} P(t) = R_d Q(t) + L \left( 1+\frac{R_d}{R_p} \right) \frac{d Q(t)}{dt} +R_d C L\frac{d^2 Q(t)}{dt^2} +P_d - \frac{L+R_p R_d C}{R_p} \frac{d P(t)}{dt} - \frac{R_d C L}{R_p} \frac{ d^2 P(t)}{dt^2} \end{align} $$
OpenFOAMを使った解析
OpenFOAM実装は、 コミュニティ版のOpenFOAM (foam-extend-4.1およびsolids4Foam-v2.1)を 参考にして実施した。
https://github.com/MA-Raza/CoronaryLumpedParameterNetworkBC
ここではソースプログラムを修正し、汎用のESI版OpenFOAM (v2506)で稼働するように 若干の変更を行った。
なお実際にはほとんど修正は不要であり一部の関数呼び出しの形式を変更する程度である。
解析モデル
直径3cm、長さ12cmの円柱を考える。円柱下端において流入速度を指定した。 円柱上端はwindkessel境界を設定した。
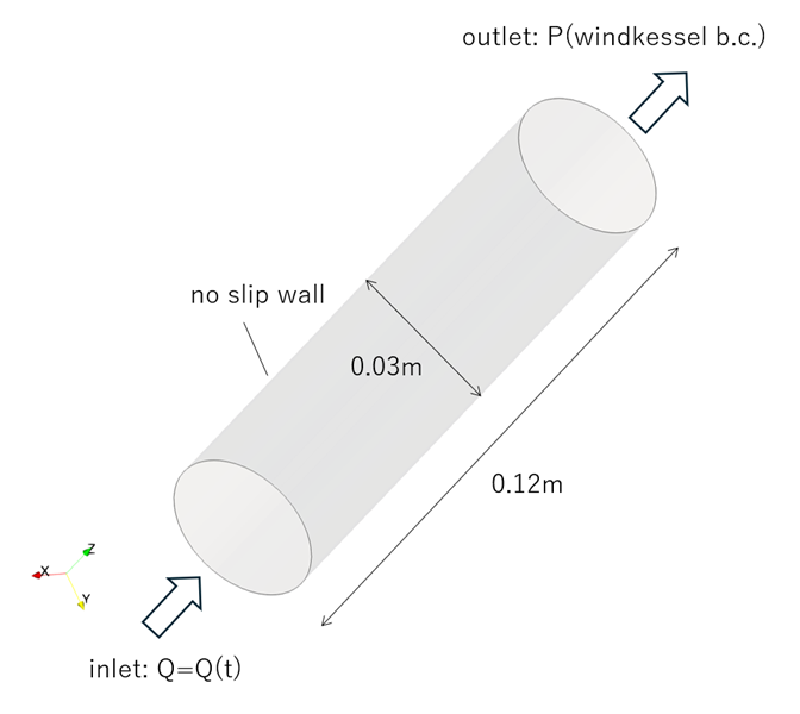
以下にメッシュ分割図を示す。

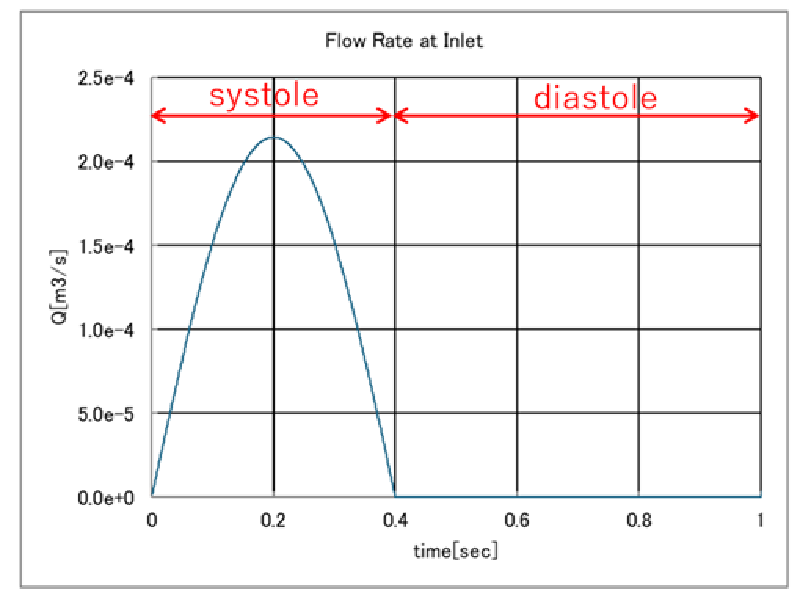
流入速度の心臓の拍動を模擬するために以下のような時間パターン(正弦関数)で設定した。
なお図中のsystoleは心臓収縮期、diastoleは心臓拡張期を示している。
流量値は1拍動当たりの平均的な心拍流量70[mL]から算出した。 ここでは心拍周期は1[sec]とした。
物性値
流体は血液を想定し、密度$\rho=1060[kg/m^3]$、粘度$\mu=0.004[Pa.s]$とした。
windkessel境界に関するパラメータは前記資料の例題値と同じとした。
3要素windkesselモデル(wk3)の係数
- 近位抵抗 $R_p=1.3997\times10^7[kg/m^4/s]$
- 遠位抵抗 $R_d=1.4152\times10^8[kg/m^4/s]$
- コンプライアンス $C=1.0\times10^{-8}[m^4s^2/kg]$
- $P_d=0$
境界条件の指定
流量は関数式を使って指定した。以下に OpenFOAMの0/U ファイルの抜粋を示す。
流速強度は心拍周期1[sec]で変動する。 心臓収縮期(0.4[sec])には正弦関数で流量が増減し、 心臓拡張期(0.6[sec])には流量ゼロとした。 またinlet境界面の流速分布形状は放物面を仮定した。
inlet
{
type codedFixedValue;
name pulse;
value uniform (0 0 0);
code
#{
const fvMesh& mesh = patch().boundaryMesh().mesh();
const scalar t = mesh.time().value();
const scalar pi = constant::mathematical::pi;
const scalar R = 0.015; // radius [m]
const scalar R2 = R*R;
const scalar area = pi * R2; // area [m2]
const scalar qmax = 2.75e-4; // [m3/s]
const scalar umax = 2.0*qmax/area;
const scalar Ts = 0.4; // systole time [sec]
const scalar Td = 0.6; // diastole time [sec]
const scalar Tp = Ts + Td; // cardiac cycle time [sec]
const scalar tfrac = fmod(t,Tp);
const scalar factor = (tfrac>Ts ? 0.0 : umax*sin(pi/Ts*tfrac));
vectorField ans(patch().size(), Zero);
forAll(ans, fi)
{
ans[fi].z() = umax * factor
* (1.0 - (pow(patch().Cf()[fi].x(),2.0)
+pow(patch().Cf()[fi].y(),2.0))/R2 );
}
operator==(ans);
#};
}
以下に OpenFOAMの0/p ファイルのwindkessel境界条件の指定例を示す。
これは時間積分が一次精度の3要素windkesselモデルである。
outlet
{
type windkesselOutletPressure;
windkesselModel WK3;
diffScheme firstOrder;
Rp 13997000; // Proximal resistance in [kgm^-4s^-1]
Rd 141520000; // Distal resistance in [kgm^-4s^-1]
C 1.0000e-08; // Compliance in [m^4s^2kg^-1]
Pd 0; // Distal pressure in [Pa]
value uniform 0;
}
解析結果
時間刻みを0.001[sec]で8[sec]に渡って解析を行った。 使用したソルバーはpimpleFoamである。 時間積分法は一次精度とした。 以下に3要素windkesselモデルを使った場合の流速ベクトル、圧力コンターの結果を示す。
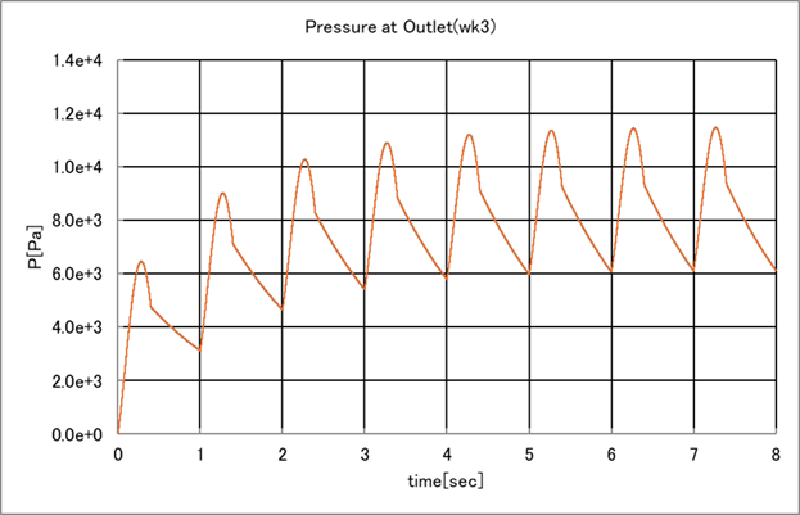
出口境界面における圧力の経時変化を調べると下図のようになった。 8周期程度でほぼ定常状態に漸近していることがわかる。
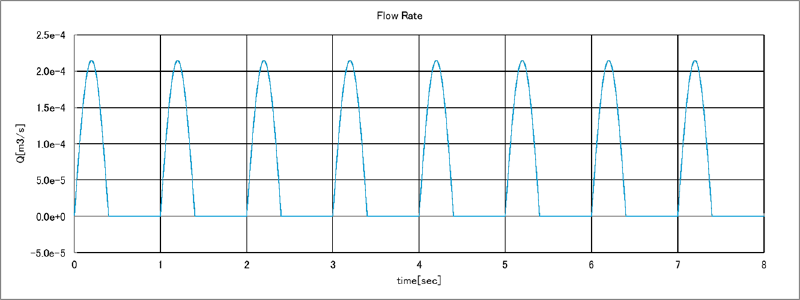
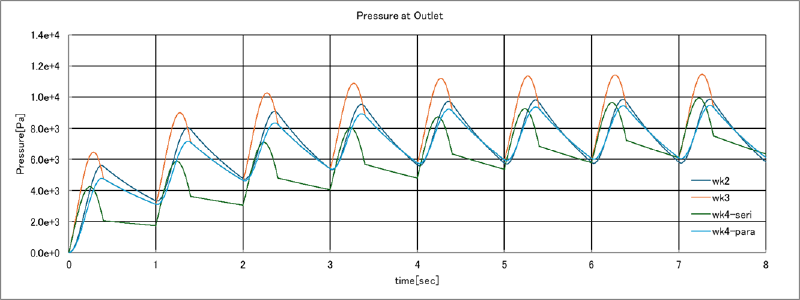
次にwindkesselモデルの全ケース(wk2,wk3,wk4-seri,wk4-para)の流量、 および出口圧力の経時変化を示す。 使用するwindkesselモデルにより圧力の変動特性が大きく異なっていることがわかる。
まとめ
openfoamにwindkesselモデルを組み込んだ計算モデルの紹介を行った。 なお今回の解析で使用したOpenFOAM関連のデータ(境界条件ソースプログラム、 解析データ)は以下からダウンロード可能である。
弊社の解析事例
弊社の流体解析事例については、下記のリンクからご覧ください.