等価な流体力ベクトルの図表示

By M.Sato

September 7, 2023

はじめに

fluentで流体解析を行う目的の一つは、物体に作用す流体力を評価することです。粘性流体の場合、全流体力は、圧力と粘性力の和として表されます。境界面に作用する流体力を積分する（すなわち足し合わせる）と一個のベクトルになります。これは流体力を等価な一個のベクトルに置き換えたものとみなすことができます。 fluentではこの等価流体力ベクトルを図として表示できないのでpythonのmatplotlibライブラリを使い表示できるようにしてみました

計算モデル

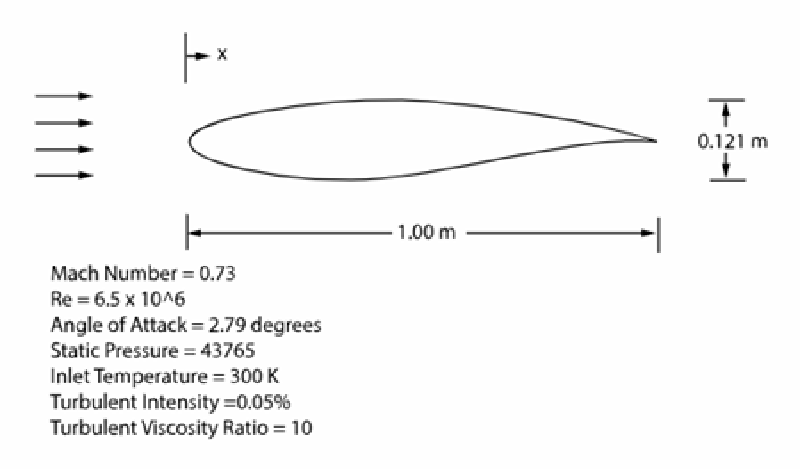
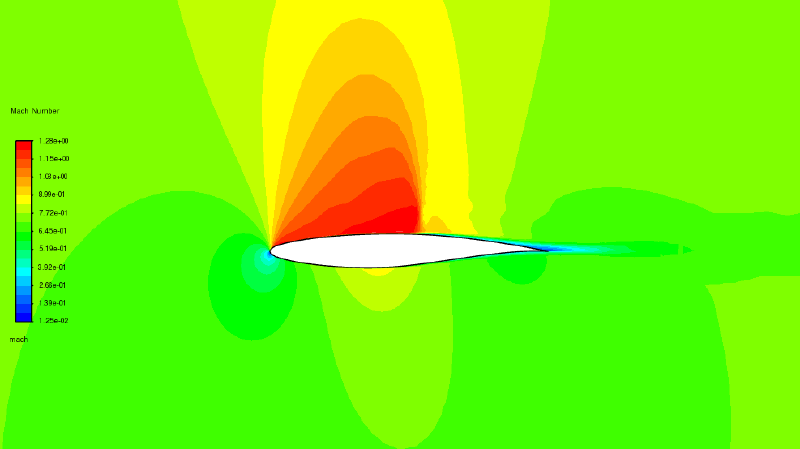
fluentのvalidattionマニュアルの検証例題17 （👈アクセスするにはAnsysユーザ－である必要があります）を使います。これはRAE2822翼型周囲を迎え角2.79度で通過する気流の計算です。マッハ数は0.73で、二次元圧縮性流体として計算しています。乱流モデルはSST $k-omega$モデルです。

モデル図

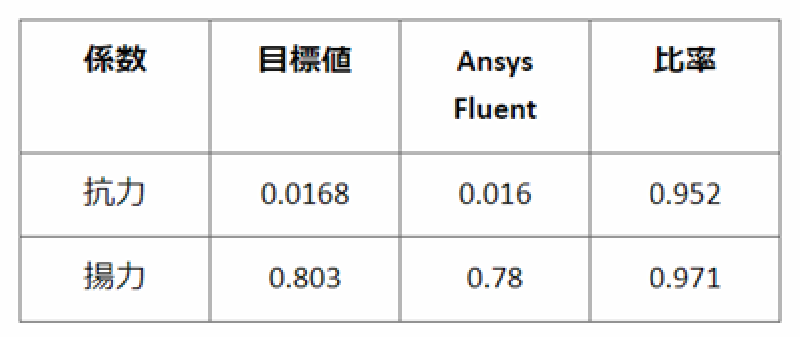
計算条件は下表のようになっています。

計算条件

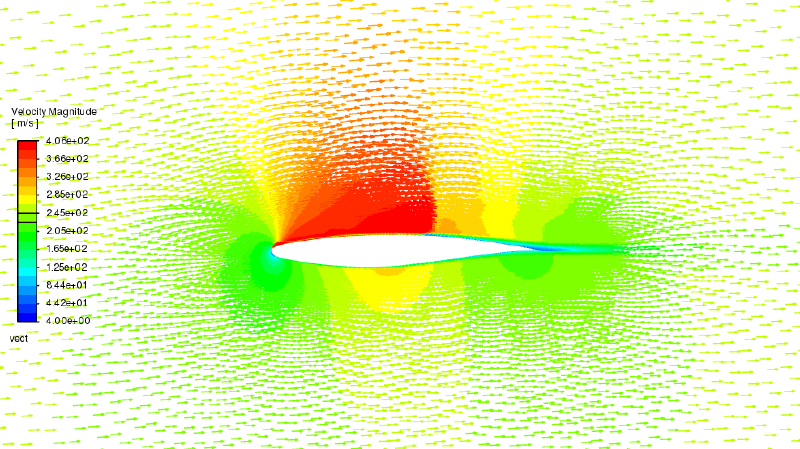
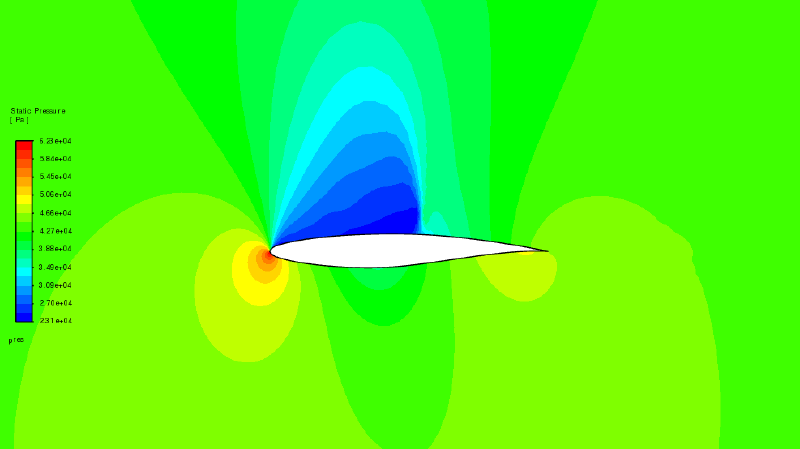
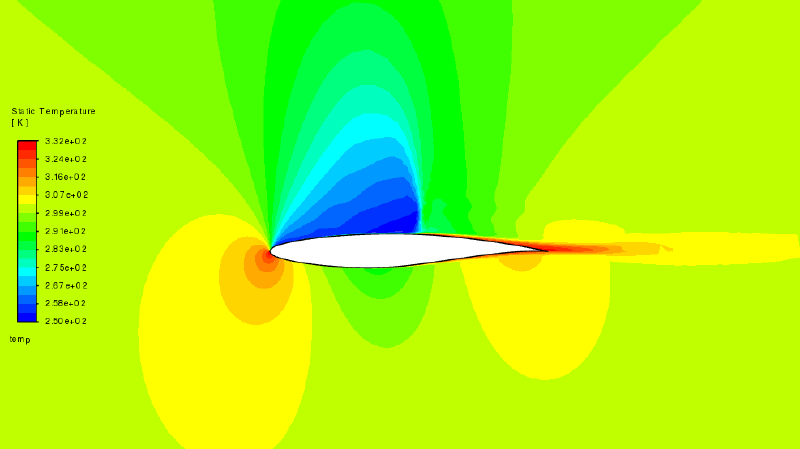
いくつかの計算結果図を示します。

メッシュ分割図

流速ベクトル図

圧力コンター図

温度コンター図

Ma数コンター図

なお、参考までに効力係数、揚力係数の実験値とfluentの計算値との比較は下表のようになっています。

作用力ベクトル図

作用力ベクトル図を表示するための手順を示します。

翼形状データの作成（もし必要な場合）
境界作用力の計算
圧力中心の計算
matplotlibを使った作図

翼形状データの作成

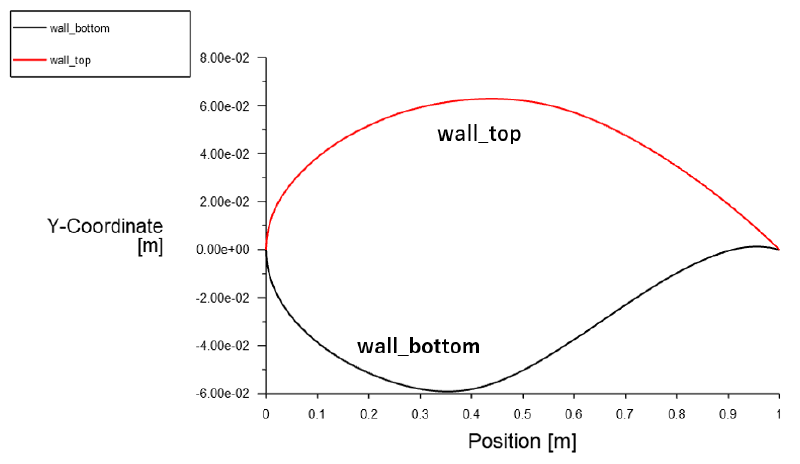
今回は、fluentのメッシュデータから翼形状データを抽出します。もし形状データが別手段ですでに利用可能なのであれば、この作業は不要です。まず、fluentのxyplot図を使い翼形状の座標データをファイルに出力します。

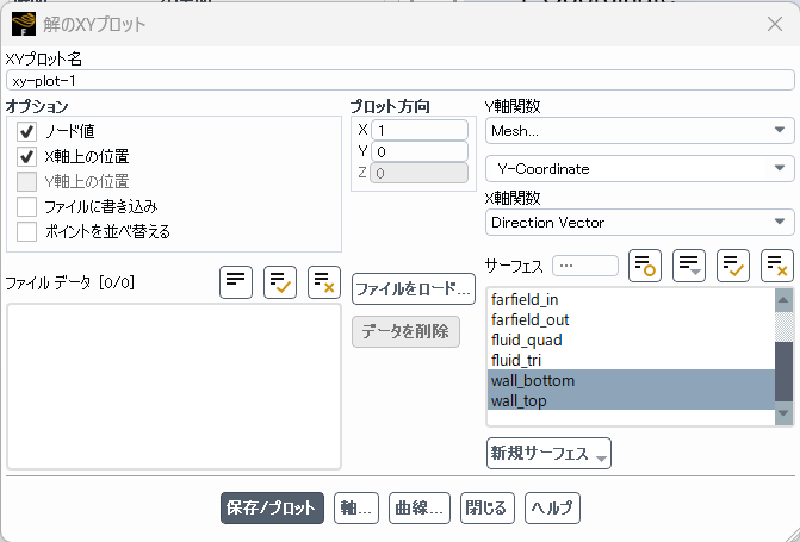
ファイル出力したデータは以下のようになっています。各行の2個の数値が$(x,y)$座標になっています。翼形状は上面(wall_top)と下面(wall_bottom)で構成されていますが、wall_top側のデータ順を逆転させて wall_bottomとwall_topデータを一筆書き可能なループデータに変換します。その際に接合部の重複データを削除します。手作業で行うと手間がかかるのでシェルスクリプト(shl)で最終翼形状データを作成します。

xyplotコマンドで出力した翼形状データ(y-coord.xy)

(title "Y-Coordinate")
(labels "Position" "Y-Coordinate")

((xy/key/label "wall_bottom")
0	0
8.19127e-06	-0.000300059
2.91103e-05	-0.000617552
6.43601e-05	-0.000952979
[snip]
0.994661	0.000187287
0.996493	8.39031e-05
0.998272	-1.10087e-05
1	-9.98777e-05
)

((xy/key/label "wall_top")
0	0
3.47302e-06	0.000303286
1.9783e-05	0.000624377
5.07541e-05	0.000963767
[snip]
0.994773	0.00102965
0.996569	0.000649873
0.998311	0.000273724
1	-9.98777e-05
)

プロット図作成用の形状データを作成するシェルスクリプト(shl)


sed -n -e '/wall_bottom/,/^)/{ /^[0-9-]/p }' y-coord.xy > _bot.dat      # wall_bottom 境界のデータを抽出

sed -n -e '/wall_top/,/^)/{ /^[0-9-]/p }' y-coord.xy | tac > _top.dat   # wall_top 境界のデータを抽出 (データ順を逆転)

cat _bot.dat _top.dat | uniq > aerofoil.txt                             # bottom側とtop側データを結合して ファイル出力

rm -f _bot.dat _top.dat                                                 # 作業データを削除

最終的に翼形状データを aerofoil.txtというファイル名で保存します。

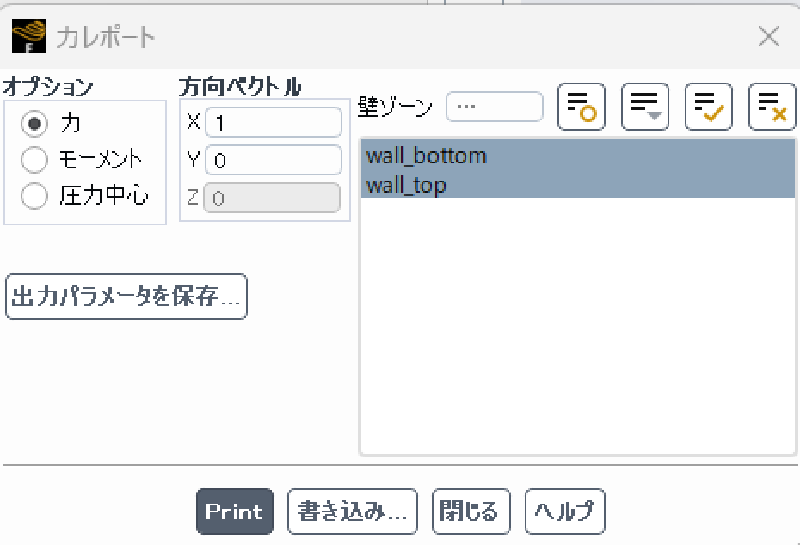
境界作用力の計算

作用力の計算入力フォーム

作用力の計算結果

図中の赤字部分が全流体力のベクトルになります。方向ベクトルを$x=1$としていますが、出力ファイルには3成分値が全て出力されています。

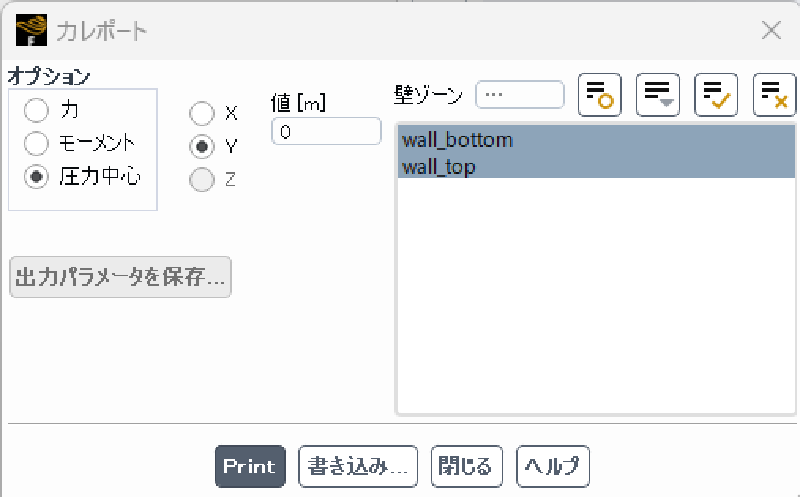
圧力中心の計算

圧力中心とは、モーメントがゼロとなるような、座標位置のことです。原点を基準にした場合のモーメントは次式で表されます。

$M_x = F_z Y - F_y Z$
$M_y = F_x Z - F_z X$
$M_z = F_y X - F_x Y$

三次元では、これらのうち2つの式をゼロとし、ユーザー指定の（拘束となる）参照平面の式を用いて、作用軸と指定された参照平面の交点を求めます。二次元では、最後の式を使い圧力中心を計算します。例えば$y=0$が翼中心線となるような二次元翼型を考えます。この場合 $y=0$という参照線上の圧力中心は、

$x = M_z/F_y$

と計算されます。この座標値は翼の揚力が作用する位置を表しています。

💡 圧力中心で使用する力、モーメントは”圧力の寄与分のみ”であり粘性力は含まれません。

圧力中心の計算入力フォーム

圧力中心の計算結果

$y=0$という参照線上の作用力中心($x$座標)は 0.36 程度であることがわかります。

matplotlibを使った作図

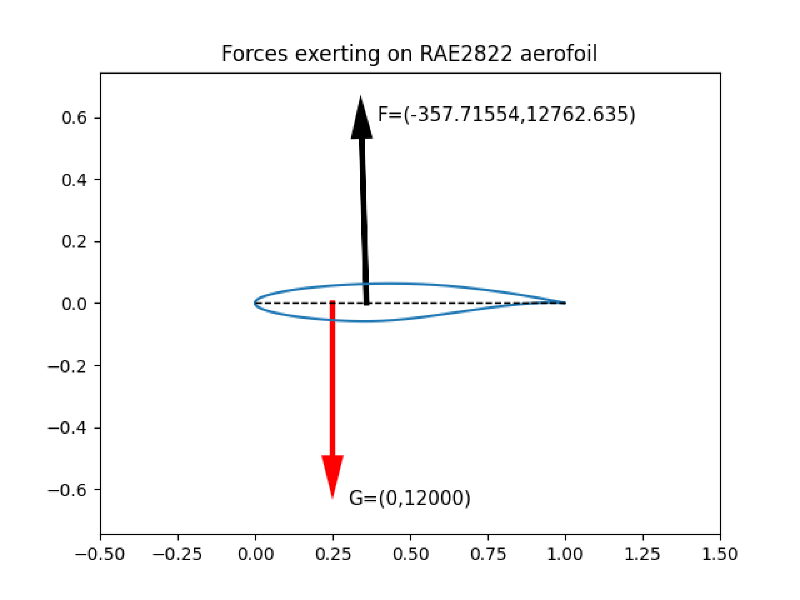
以下に翼型に作用する力をベクトルを表示した例を示します。ここでは以下の仮定を行っています。

力の作用点は全流体力（圧力＋粘性力）から計算すべきですが、ここでは圧力中心を使用(粘性力の影響は小さいと仮定)
翼に作用する重力、およびその作用位置は、本来、翼内部の密度分布から算出すべきですが、ここでは適当に仮定

作図を行うpythonスクリプトの例を示します。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure, show

# 翼表面作用力
fx = -357.71554    # x方向力
fy = 12762.635     # y方向力
cpx = 0.3594281    # x作用点
cpy = 0            # y作用点

scale = 1/20000  # 表示図内に収まるように適当にスケーリング

# 翼体積作用力(重力) -- これは適当に設定した値です(仮想値)
gx = 0        # x方向力     
gy = 12000    # y方向力         
gpx = 0.25    # x作用点         
gpy = 0       # y作用点      

# ----> 翼形状データを読み込む
data = np.loadtxt("aerofoil.txt")
x = data[:,0]
y = data[:,1]
# <----

plt.figure()
plt.axis('equal')  # アスペクト比を保つ

plt.plot(x, y) # 翼形状をプロット

# 翼中心線を破線で表示
plt.plot([0,1], [0,0], linestyle='--', linewidth=1.0, color="black" )

# 翼に作用する流体力ベクトルをプロット
plt.arrow(cpx, cpy, fx*scale, fy*scale, facecolor='black', edgecolor='black', alpha=1,
     length_includes_head=True, shape='full', overhang=0,
     head_width=0.05, head_length=0.10,
     linewidth=3 )

# 矢印の先端位置を求める
tipx = cpx + fx*scale + 0.05
tipy = cpy + fy*scale

# 作用力値を表示
plt.text(tipx, tipy, f'F=({fx},{fy})', fontsize=11,
     horizontalalignment='left',
     verticalalignment='top',
     clip_on=False)

# 翼に作用する重力ベクトルをプロット(仮想値)
plt.arrow(gpx, gpy, gx*scale, -gy*scale, facecolor='red', edgecolor='red', alpha=1,
     length_includes_head=True, shape='full', overhang=0,
     head_width=0.05, head_length=0.10,
     linewidth=3 )

# 矢印の先端位置を求める
tipx = gpx + gx*scale + 0.05
tipy = gpy - gy*scale

# 作用力値を表示
plt.text(tipx, tipy, f'G=({gx},{gy})', fontsize=11,
     horizontalalignment='left',
     verticalalignment='top',
     clip_on=False)

plt.xlim([-0.5,1.5])
plt.ylim([-1.0,1.0])

plt.title("Forces exerting on RAE2822 aerofoil")
plt.grid(False)
plt.show()

まとめ

fluentで計算された流体力を力の作用線上にベクトルとして表示する方法を記述しました。なお、ここでは示しませんでしたが、外部モーメントがある場合には円弧の矢印を使って図表示することもできると思います。流体力の表示を工夫することで分かりやすい図を作成してみてください。

👉 本記事で使用したデータやプログラムを実際に試したい場合は、弊社までお問い合わせください。

弊社の解析事例

弊社の流体解析事例については、下記のリンクからご覧ください．

👉 解析事例のご紹介 FLUENT

👉 流体解析実績及び事例

参考文献

P.H.Cook, M.A. McDonald, M.C.P.Firmin, “AEROFOIL RAE 2822 Pressure Distribution and Boundary Layer and Wake Measurements”.AGARD Advisory Report.No. 138.1979.
S.J.Kline, B.J.Cantwell, G.M.Lilley, “1980-81 AFOSR-HTTM-Stanford Conference on Complex Turbulent Flows: Comparison of Computation and Experiment”, Stanford University, Stanford, Calif., 1982.