毛細管現象のシミュレーション
By M.Sato
概要
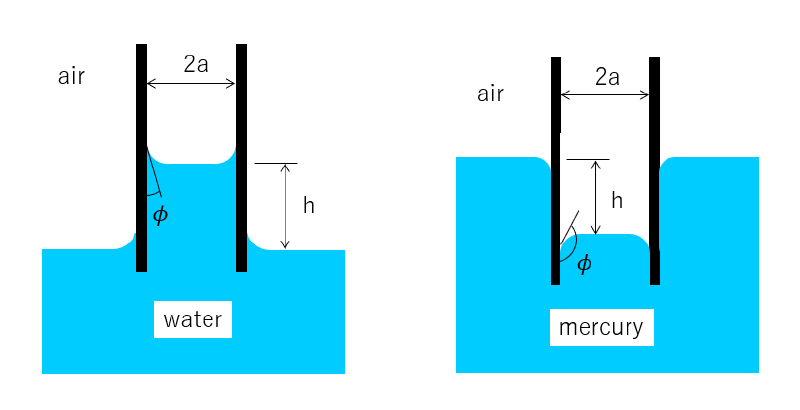
水たまりに微小な円筒空洞があるパイプ(毛管)を挿入すると毛管内の水面位置が上昇する。
また、水銀(常温で液体)たまりに毛管を挿入すると毛管内の自由表面位置は周辺の液面位置よりも下降している。
これらは毛細管現象として知られている。
ここでは、Ansys Fluentを使い毛細管現象のシミュレーションを行ってみた。
また、自由表面(メニスカス)形状の理論解を導いてみた。
👉 Youtube動画もありますので、ご参考ください。
Fluentを使った解析
Fluentでは自由表面に作用する表面張力係数および、自由表面が固体壁と接する場合の接触角を指定した解析が可能である。
ここでは、液体が水の場合と水銀の場合を対象にしてVOF法を使ってシミュレーションを行ってみた。
なお、形状の対称性を考慮し軸対称モデルを使って計算を行った。
水-空気界面の毛管上昇
毛管の半径$a$が、$1$mm, $2$mm, $4$mmの3ケースについて計算を行った。
物性値
ここでは流体物性値を以下のように設定した。
なお、今回の計算では静止状態の流体の平衡を計算することになるため、 計算の安定性を考慮して粘度値は実際の値を1000倍したものにしている。
$$ \begin{array}{ll} 空気密度:&\rho_{air} = 1.2 [kg/m^3] \\ 空気粘度:&\mu_{air} = 1.8\times10^{-2} [Pa.s] \\ 水密度:&\rho_{water} = 1000 [kg/m^3] \\ 水粘度:&\mu_{water} = 1.0 [Pa.s] \\ 水-空気間の表面張力: &\sigma = 0.072 [N/m] \\ 接触角: &\phi = 30 [deg] \end{array} $$
解析領域
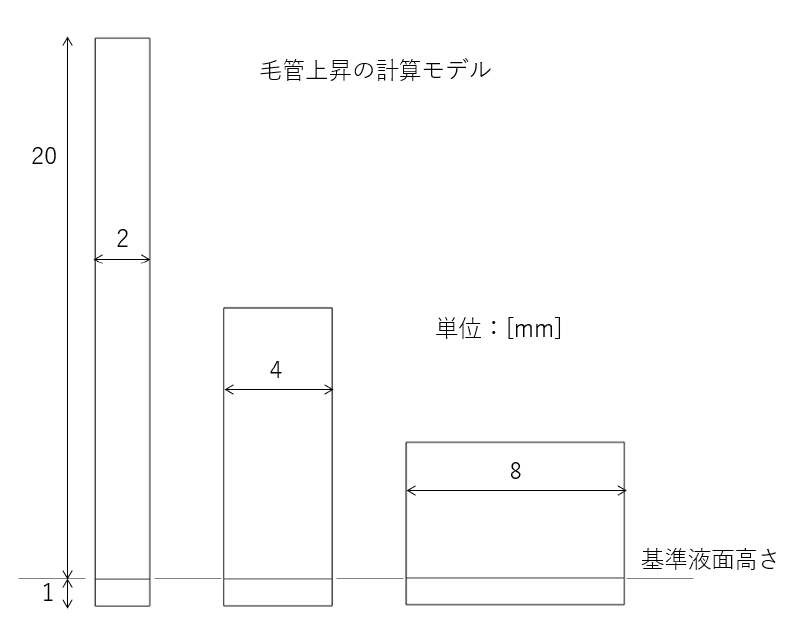
基準水面位置からの毛管上昇量の概算値を推定し解析領域を設定した。
毛管上昇量の推定値$h$は次式で表される。 これは自由表面形状が球面であると仮定した時の簡易式である。
$$ h = \frac{ 2 \sigma \cos\phi } {\rho g a} $$
ここで、 $\sigma$:表面張力係数、$\phi$:接触角、$\rho$:液体密度、$g$:重力加速度、$a$:毛管の半径
これから液面上昇量を推定すると以下のようになった。
| 半径a[mm] | 上昇量h[mm] |
|---|---|
| 1 | 12.7 |
| 2 | 6.36 |
| 4 | 3.18 |
メッシュ分割を以下に示す。セルサイズはすべて同じ(辺長0.1mmの四角形)にしている。
解析結果
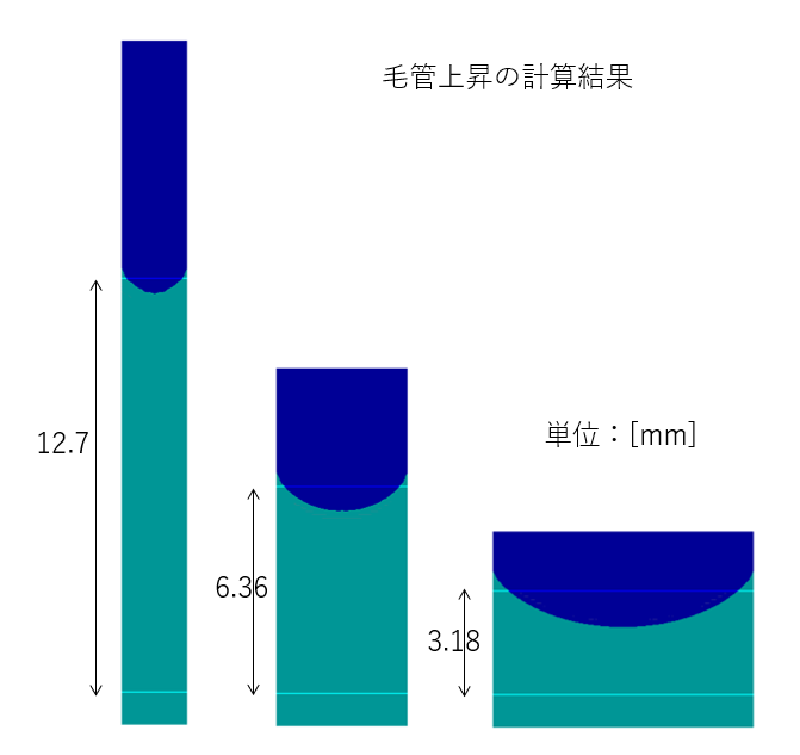
計算は非定常で行い、解が定常状態に漸近するまで実施した。 最終的な自由表面形状を以下に示す。
図中には簡易式で推定した液面位置も表示している。 液面の上昇量は概ね推定値に一致していることがわかる。
水銀-空気界面の毛管下降
毛管の半径$a$が、$1$mm, $2$mmの2ケースについて計算を行った。
物性値
ここでは流体物性値を以下にように設定した。
なお、今回の計算では静止状態の流体の平衡を計算することになるため、 計算の安定性を考慮して粘度値は実際の値を1000倍したものになっている。
$$ \begin{array}{ll} 空気密度:&\rho_{air} = 1.2 [kg/m^3] \\ 空気粘度:&\mu_{air} = 1.8\times10^{-2} [Pa.s] \\ 水銀密度:&\rho_{mercury} = 13600 [kg/m^3] \\ 水銀粘度:&\mu_{mercury} = 1.5 [Pa.s] \\ 水銀-空気間の表面張力: &\sigma = 0.48 [N/m] \\ 接触角: &\phi = 140 [deg] \end{array} $$
解析領域
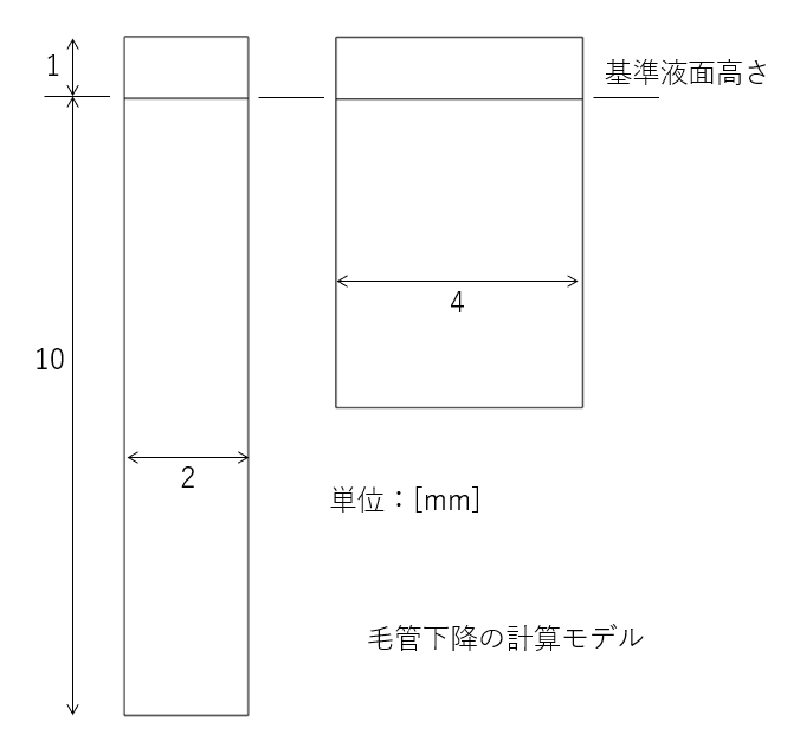
基準液面位置からの毛管下降量の概算値を推定し解析領域を設定した。
毛管下降量の推定値$h$は次式で表される。 これは自由表面形状が球面であると仮定した時の簡易式である。
$$ h = \frac{ 2 \sigma \cos \phi } {\rho g a} $$
ここで、 $\sigma$:表面張力係数、$\phi$:接触角、$\rho$:液体密度、$g$:重力加速度、$a$:毛管の半径
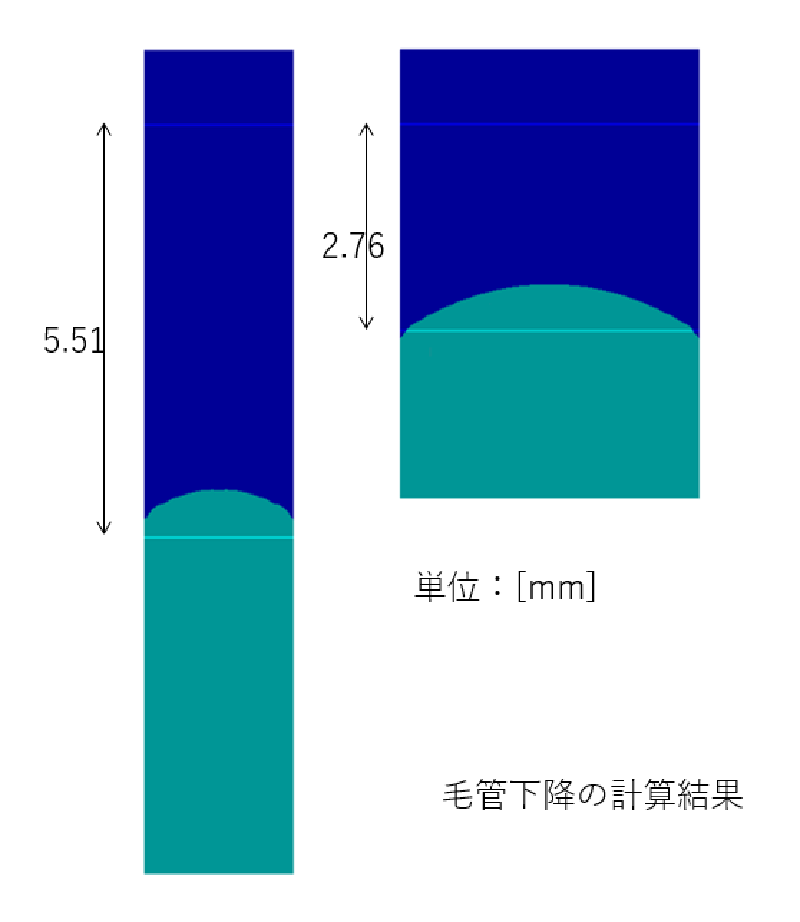
| 半径a[mm] | 下降量h[mm] |
|---|---|
| 1 | -5.51 |
| 2 | -2.76 |
メッシュ分割を以下に示す。 セルサイズはすべて同じ(辺長0.1mmの四角形)にしている。
解析結果
計算は非定常で行い、解が定常状態に漸近するまで実施した。
最終的な自由表面形状を以下に示す。 液面の下降量は概ね推定値に一致していることがわかる。
メニスカス形状の理論解
界面に作用している圧力は、表面張力係数と曲率の積に比例している。
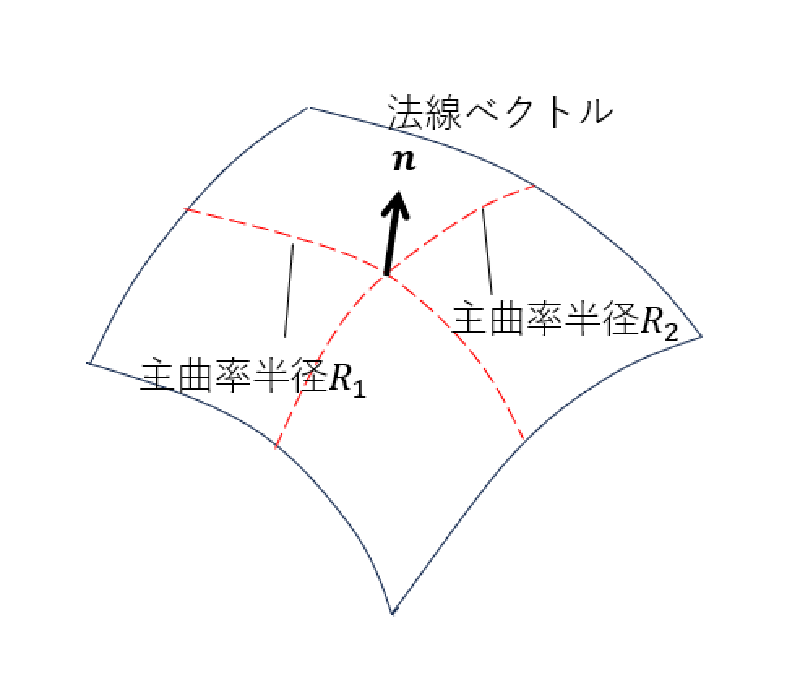
3次元空間では界面形状は曲面となるが、 曲面上の任意点における曲率はその任意点を通過する直交する2平面を想定し、 それらの平面内の曲率の和で表される。 なお、曲率とは曲率半径の逆数である。
2平面は直交していれば任意にとることができるが、 曲率が最大、最小となるように選択することが可能である(主曲率)。
この場合、表面張力により生成される圧力差(ラプラス圧)$\Delta p$は次式で表される。
$$ \Delta p = \sigma \left( \frac{1}{R_1} + \frac{1}{R_2} \right) $$
ここで、$\Delta p$:圧力差、$\sigma$:表面張力係数、$R_1,R_2$:主曲率半径
次に毛管上昇で形成される自由表面形状を考える。
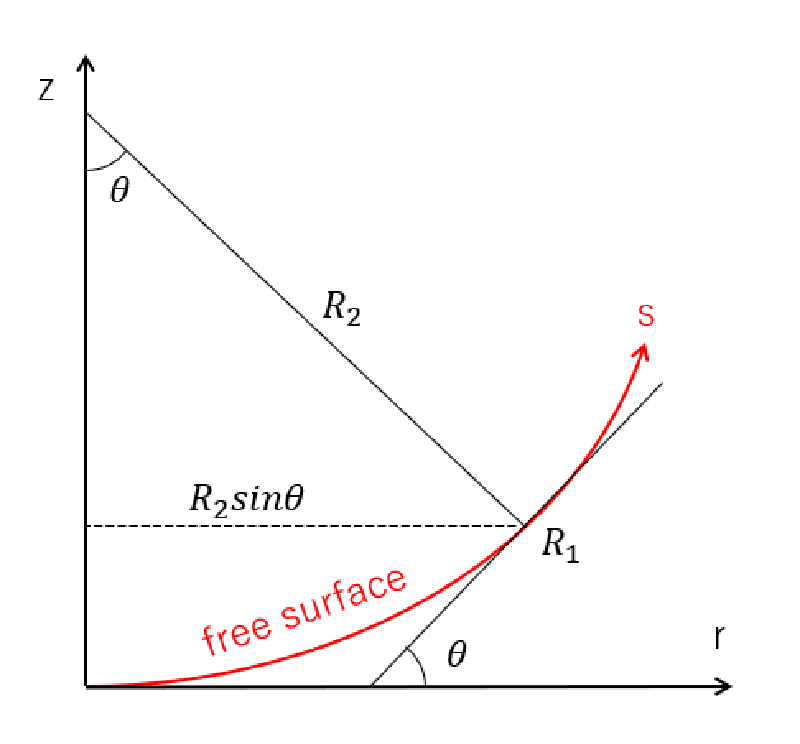
形状は軸対称であることから鉛直断面内を対象としてよい。 自由表面の最下端を原点とし鉛直方向にz軸、半径方向にr軸を設置する。
自由表面の曲率について考える。
一つは主曲率のr-z平面内の曲線形状から算出されるものである($\kappa_1$)。
もう一つはz軸周りの回転に伴う曲面から算出されるものである($\kappa_2$)。
$r, z$座標で表現すると次式で表される。
$$ \begin{array}{l} \kappa_1 = \frac{1}{R_1}= \frac{ d^2 z / d r^2 }{ (1+(d z/d r)^2 )^{3/2} } \\ \kappa_2 = \frac{1}{R_2}= \frac{ dz/ dr }{ r(1+(d z/d r)^2 )^{1/2}} \end{array} $$
静止状態の液体には静水圧が作用していることから、圧力の釣り合い式を立てると次式が得られる。
$$ \rho g z - \sigma \left[ \frac{ d^2 z / d r^2 }{ (1+(d z/d r)^2 )^{3/2} } + \frac{ dz/ dr }{ r(1+(d z/d r)^2 )^{1/2}} \right] = - \frac{2 \sigma}{R_0} $$
ここで $R_0$は最下端点(対称軸上)における曲率半径である。
この微分方程式を解くことで自由表面形状が得られることになるが、 変数を別のものにすることでもっと簡潔な表現が可能である。
自由表面上の任意点での勾配角を$\theta$ととることで、次に示す微分方程式が得られる。
$$ \frac{d r}{d s} = \sin \theta \ \frac{d z}{d s} = \cos \theta $$
$$ R_1 = \frac{ds }{d \theta} , R_2 = \frac{r}{ \sin \theta} $$
$$ \rho g z - \sigma \left[ \frac{d \theta}{d s}+\frac{ \sin \theta }{r} \right] = - \frac{2 \sigma}{R_0} $$
ここで $s$は自由表面曲線に沿う長さである。整理すると
$$ \frac{d r}{d s} = \sin \theta \ \frac{d z}{d s} = \cos \theta $$
$$ \frac{d \theta}{d s} = \frac{2}{R_0} - \frac{\sin \theta}{r} + \frac{z}{R_c^2} $$
ここで $R_c=\left( \frac{\sigma}{\rho g} \right)^{1/2}$はキャピラリ長さと言われるものである。
上に示した式は$r,z,\theta$に関する連立微分方程式になっている。
無次元化された方程式
代表長さを$L$として無次元方程式を導く。
($r^\ast = r/L, z^\ast=z/L, s^\ast = s/L$)
$$ \begin{align} \frac{d r^\ast}{d s^\ast}&= \sin \theta \\ \frac{d z^\ast}{d s^\ast}&= \cos \theta \\ \frac{d \theta}{d s^\ast}&= \frac{2}{R_0^\ast} - \frac{\sin \theta}{r^\ast} + Bo z^\ast \end{align} $$
ここで $Bo = \frac{L^2}{R_c^2}= \frac{\rho g L^2}{\sigma}$ はボンド数と言われているものである(エトベス数とも言われる)。
ボンド数は重力と表面張力の相対的な大きさを表しており表面張力の効果が顕著な場合、Bo数は小さくなる。
この式よりメニスカス形状はボンド数が支配パラメータとなっていることがわかる。
上に示した連立微分方程式を $r^\ast,z^\ast, \theta$を未知変数として積分すれば解が得られる。
境界条件は$z^\ast=r^\ast=s^\ast=0$である。 なお$r\rightarrow 0$の時、$\frac{\sin \theta}{r}\rightarrow \frac{1}{R_0}$となることに注意。
メニスカス形状を計算するjuliaプログラムを以下に示す。
ここでは$s$(および$r$)の初期値には微小値を設定した。
using ParameterizedFunctions, DifferentialEquations
using Printf
rho = 1000 # densoty of liquid [kg/m3]
grav = 9.81 # gravity accerlation [m/s^2]
sigma = 0.072 # surface tension [N/m]
Cleng = 1e-3 # characteristic length [m]
Radius = 1e-3 # radius of pipe [m]
#Radius = 2e-3 # radius of pipe [m]
#Radius = 5e-3 # radius of pipe [m]
#Radius = 10e-3 # radius of pipe [m]
#Radius = 20e-3 # radius of pipe [m]
Rc2 = sigma/(rho*grav)
Rc = sqrt(Rc2) # capillary-length [m]
Bo = Cleng^2/Rc2 # Bond number
tiny = 1e-12
R0 = 1.0 * Radius # center radious [m]
R0 /= Cleng # non-dimensioned center radious
# 常微分方程式の定義
eqns = @ode_def capillary begin
dX = cos(T)
dZ = sin(T)
dT = 2/R0 - sin(T)/X + Bo*Z
end R0 Bo
# 問題定義
u0 = [tiny; 0; asin(tiny/R0)] # 初期 r, z, t
tspan = (tiny, 10.0) # 時間積分期間
p = [ R0, Bo ]
prob = ODEProblem(eqns,u0,tspan,p)
# 計算
@time sol = solve(prob,Tsit5(),reltol=1e-8,abstol=1e-8)
(nrow,ncol)=size(sol)
times=zeros(Float64,0)
xvals=zeros(Float64,0)
zvals=zeros(Float64,0)
thetas=zeros(Float64,0)
@printf("j : time xval zval theta\n")
for j=1:ncol
time = sol.t[j]
xval = sol.u[j][1]
zval = sol.u[j][2]
theta = sol.u[j][3]
append!(times,time)
append!(xvals,xval)
append!(zvals,zval)
append!(thetas,theta)
@printf("j=%d : %16.8e %16.8e %16.8e %16.8e\n",
j,time,xval,zval,theta)
end
計算例
毛管の半径$a$を $1,2,5,10,20[mm]$に変化させて自由表面形状を計算してみた。 流体は空気と水である。
なお、計算に際して中心軸上(自由表面の最下端)の曲率$R_0$を入力パラメータと して指定する必要がある。ここでは、$R_0=a$と仮定して計算を行った。
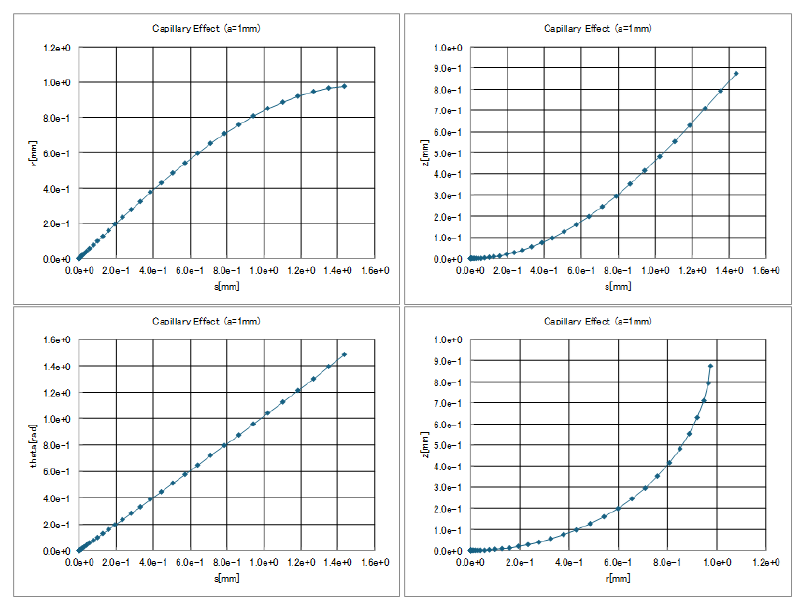
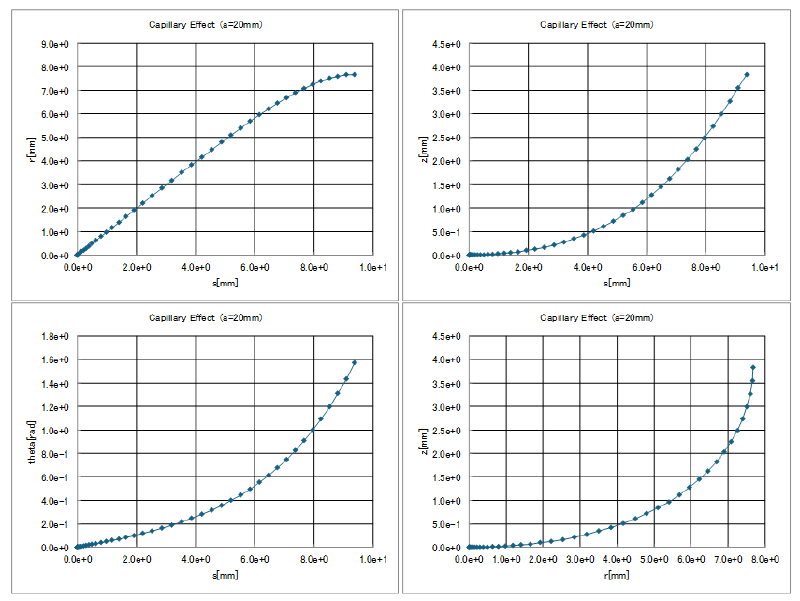
毛管半径 $a=1[mm]$の場合の計算結果を以下に示す。
4個のグラフは、$r(s), z(s), \theta(s), z(r)$の関係を表している($z(r)$は実際の自由表面形状に対応)。
$\theta(s)$ のグラフを見るとほぼ直線になっていることがわかる。
これは自由表面形状が円形に類似していることを表している。
次に毛管半径 $a=20[mm]$の場合の計算結果を以下に示す。
$\theta(s)$ のグラフを見ると対称軸付近でメニスカス形状が平坦化していることがわかる。
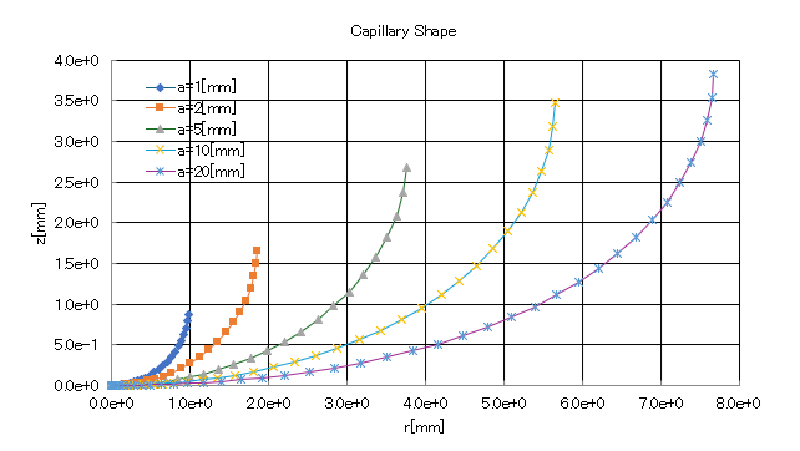
5種類の毛管に対して得られた自由表面形状$z(r)$を比較するために重ねて図表示したグラフを示す。
この図からも毛管径が小さい場合は自由表面形状は円形(すなわち球形)に近いのに対して 毛管径が大きい場合には中心付近が平坦化することがわかる
注意点
今回提示した計算手法では予め、最下点での曲率半径$R_0$を指定した上で自由表面形状を計算している。
壁面での接触角$\phi$は計算された$\theta$値が$(90-\phi)$となる半径位置を求めることで解が得られることになる。
また液面上昇高さ $h$ は基準の自由表面高さから、メニスカス最下端までの距離と定義され、 $h=\frac{2 \sigma}{\rho g r_0}$と計算される(これは正確な値である)。
実際的に応用するには毛管径と接触角を与えて自由表面を計算することが望まれるが、これについては宿題としておく。
まとめ
静止状態の液面で観察される自由表面(メニスカス)形状を、Fluentを使い計算してみた。 また正確なメニスカス形状を計算するための手法を示した。
弊社の解析事例
弊社の流体解析事例については、下記のリンクからご覧ください.