ダイラタント流体の流れ
By M.Sato
概要
流体の運動は粘度の影響を受ける。
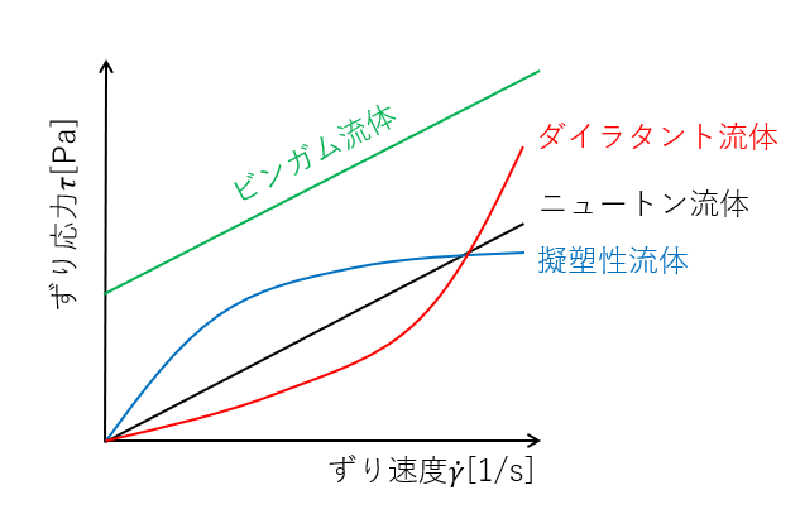
粘度はずり応力（せん断応力）とずり速度（せん断速度）の比として定義される。 代表的な流体のずり速度とずり応力の関係を以下の図に示す。
ダイラタント流体とはずり速度の増加に伴い、ずり応力が急激に増加する非ニュートン流体のことである（すなわち粘度が急激に増加する）。 身近な例だと片栗粉を水に溶かしたものが代表的なダイラタント流体である。
模式図
今回は、ダイラタント流体を対象にして、簡単な形状の流路を想定し流れ場の理論解を導いた。
また、Ansys Fluentを使って計算を行い、 理論解と計算値が一致していることをわかった。
平行平板間の流れ
解析領域
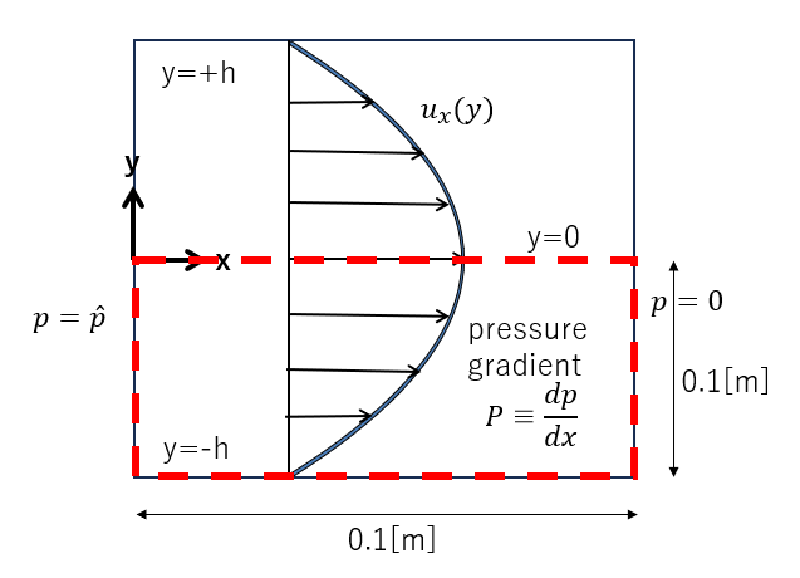
間隔 $2h$の平行平板間をダイラタント流体が流動するとし２次元モデルを作成した。
対称性を考慮して下半分の領域のみを解析対象領域としている。
解析領域
理論解
$x$方向の運動方程式は以下のようになる。
$$ 0 = -\frac{dp}{dx} + \frac{d}{dy}\left( \mu \frac{du}{dy} \right) \tag{1} $$
せん断速度は1次元流れであることから $\dot{\gamma}=\frac{du}{dy}$と簡略化される。
簡単のため $P=\frac{dp}{dx}$とおいて、 運動方程式を積分する。なお粘度式には後述のコーンスターチ実験式を想定している。
$$ \tau = \mu \frac{du}{dy} =\frac{1}{A}\log\left( \frac{B}{B-\dot{\gamma}} \right) = Py + const \tag{2} $$
constは積分定数であり、$y=0$で$\tau=0$であることから$const=0$となる。 $\frac{du}{dy}$に関して整理すると次式が得られる。
$$ \frac{du}{dy} = B\left[ 1 - \exp(-APy) \right] \tag{3} $$
$y$について積分すると
$$ u(y) = B\left[ y+C +\frac{1}{AP} \exp(-APy) \right] \tag{4} $$
$C$は積分定数であり、$y=-h$で $u=0$であることから次式が得られる。
$$ 0 = B\left[ -h+C +\frac{1}{AP} \exp(APh) \right] \tag{5} $$
これから$C$を消去すると流速分布$u(y)$が得られる。
$$ u(y) = B\left[ y+h +\frac{1}{AP} \left\{ \exp(-APy)-\exp(APh) \right\} \right] \tag{6} $$
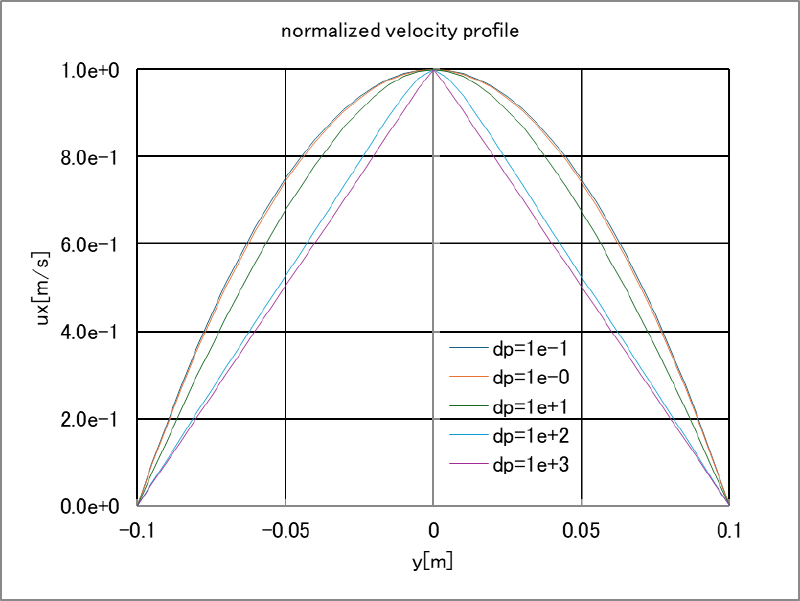
流速$u(y)$の大きさは流路の圧力勾配によって変化するが、 最大流速値で正規化して最大値が1となるようにすると流速分布は以下のようになる。
圧損値が大きくなり、せん断速度が増加すると流体は高粘度になり、 最終的に流路中央が最大流速となる三角形状の流速分布に漸近していることがわかる。
正規化流速分布
解析モデル
fluentを使い解析を行った。解析に使用したメッシュ分割を示す。
メッシュ
物性値
物性値は以下の値を使用した。
-
密度
$$ \rho = 1000\;[kg/m^3] $$
-
粘度
$$ \begin{align} \mu(\dot{\gamma}) &=\frac{1}{A\dot{\gamma}}\log\left( \frac{B}{B-\dot{\gamma}} \right)\;[Pa.s] \notag \\ A &= 0.2 \;[1/Pa] \notag \\ B &= 18 \;[1/sec] \notag \end{align} $$
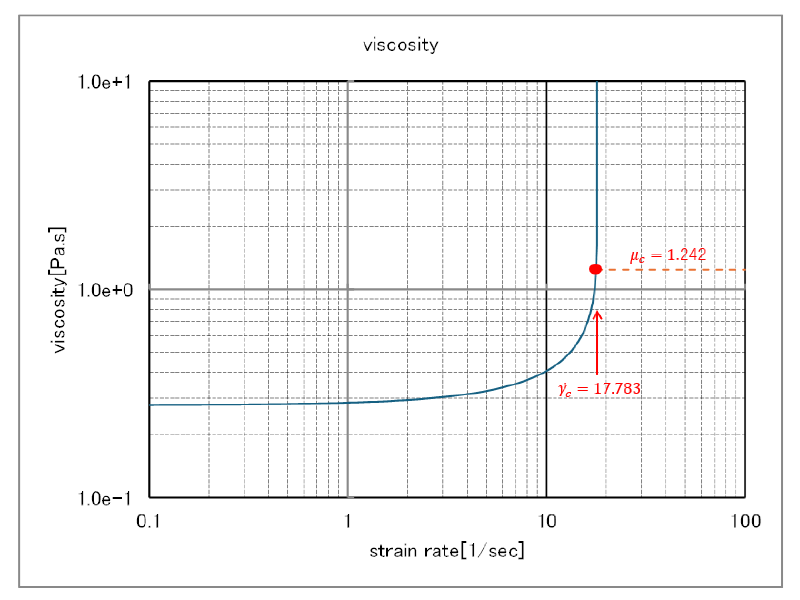
定数$A$,$B$はコーンスターチを使った実験値から得られたものである。
なお、実際の計算ではせん断速度の上限値($\dot{\gamma_c}$)を設定し、 この図上限値を超えた場合には粘度が一定($\mu_c$)になると仮定した。
粘度グラフ
境界条件として流出入境界の静圧を指定した。 圧損が$0.1$[Pa]のケースを"dp01"、$15$[Pa]のケースを"dp15"とした。
- case-dp01 : $p_{inlet}=0.1\;[Pa],\hspace{1cm}p_{outlet}=0\;[Pa]$
- case-dp15 : $p_{inlet}=15\;[Pa],\hspace{1cm}p_{outlet}=0\;[Pa]$
解析結果
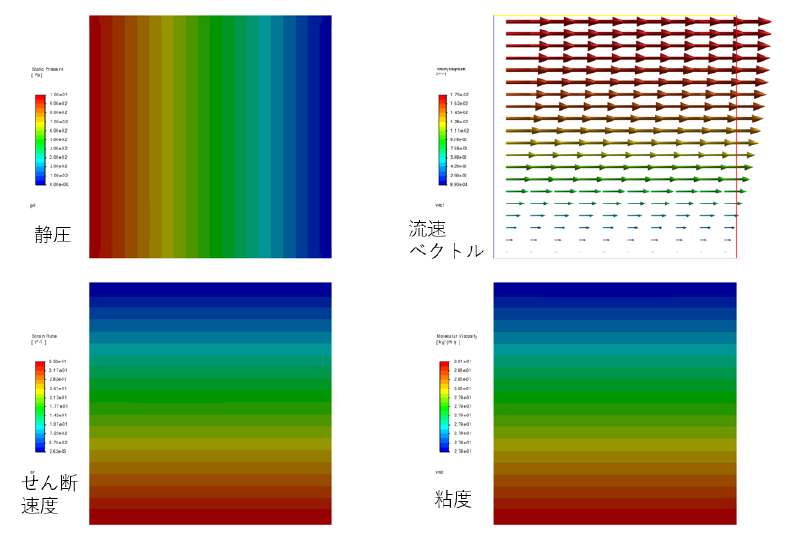
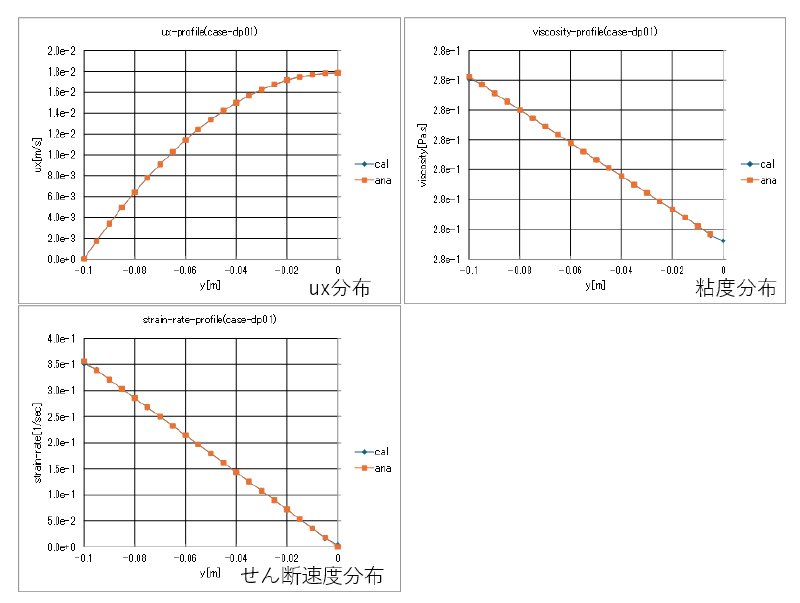
case-dp01（圧損dp=0.1[Pa]の場合）
solution-dp01の結果
出口境界における各物理量の分布を示す。 計算結果と理論解はよく一致していることがわかる。
xyplot-dp01の結果
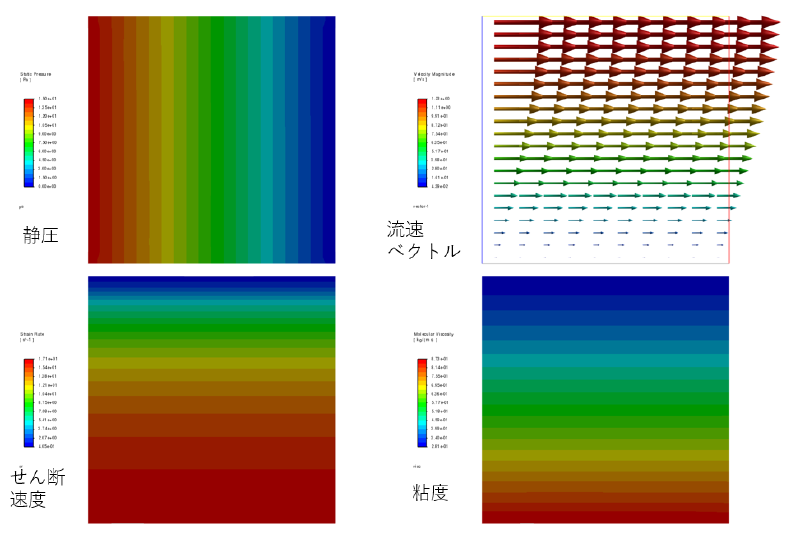
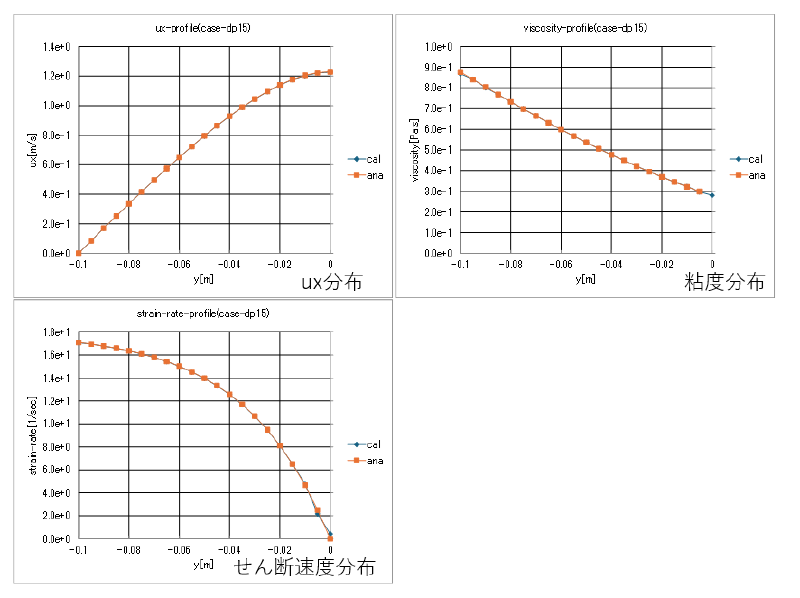
case-dp15（圧損dp=15[Pa]の場合）
solution-dp15の結果
このケースでは圧損が大きくなっており、せん断速度が増加し、それに伴い粘度も増大している。
流速分布を見ると対称面(y=0)付近を除き流速はほぼ線形分布になっていることがわかる。
ニュートン流体では放物線分布になるのに対して、分布形状が大きく異なることがわかる。
xyplot-dp15の結果
同心二重円筒間の流れ
解析領域
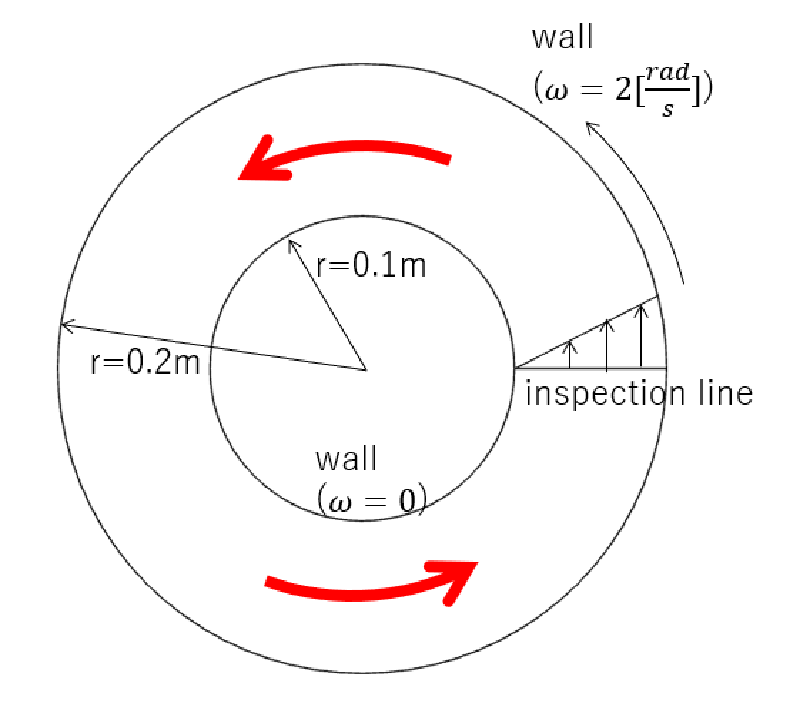
半径$r=0.1,0.2[m]$の円筒に挟まれた領域の流れを考える。
内側の円筒壁が静止しており、外側の円筒壁が$2[rad/s]$で回転しているとする。 解析対象を以下に示す。
解析対象
理論解
定常流れで半径方向流速$u_r=0$、また物理量は$\theta$方向に不変、すなわち $\frac{d}{d\theta}=0$とする。 $r,\theta$方向の運動方程式は以下のようになる。
$$ \begin{align} -\frac{u_\theta^2}{r} = - \frac{1}{\rho}\frac{d p}{d r} \tag{7} \\ \frac{d}{dr} \left[ r^2 \tau_{r\theta} \right] = 0 \tag{8} \end{align} $$
せん断応力$\tau_{r\theta}$は以下のように表せることに注意し
$$ \tau_{r\theta} = \frac{1}{A}\log\left( \frac{B}{B-\dot{\gamma}} \right) \tag{9} $$
(9)式を考慮して(8)式を$r$について積分すると次式が得られる。 ここで$C$は積分定数である。
$$ \frac{r^2}{A}\log\left( \frac{B}{B-\dot{\gamma}} \right) = C \tag{10} $$
極座標系$(r,\theta)$におけるせん断速度は次式で表される。
$$ \dot{\gamma} = r\frac{\partial }{\partial r}\left( \frac{u_\theta}{r} \right) + \frac{1}{r}\frac{\partial u_r}{\partial \theta} = \frac{ \partial u_{\theta}}{\partial r} - \frac{u_{\theta}}{r} \tag{11} $$
回転角速度を$\omega$と表すと $u_{\theta}(r)=r\omega(r)$となる。 従って上記のせん断速度は次式となる。
$$ \dot{\gamma} = r \frac{d \omega}{ d r} \tag{12} $$
これを(10)式に代入して整理すると次式が得られる。
$$ \frac{d \omega}{dr} = \frac{B}{r} \left[ 1 - \exp\left(-\frac{AC}{r^2} \right) \right] \tag{13} $$
$r$について積分すると次式が得られる。
$$ \omega = B \log r - \frac{B}{2} E_1\left( \frac{AC}{r^2} \right) +D \tag{14} $$
ここで、$D$は積分定数、 $E_1$は指数積分と呼ばれる関数であり次式で定義される。 $E_1$は単純な初等関数では表すことができず、数値的に計算して求めることになる。
$$ E_1(x)=\int_x^\infty \frac{ e^{-\xi}}{\xi} d\xi \tag{15} $$
(14)式には積分定数$C,D$が含まれているが、境界条件 $\omega(r=R_1)=0$ および$\omega(r=R_2)=2$ からこれらの値を決定する。
$$ \begin{align} 0 = B \log R_1 - \frac{B}{2} E_1\left( \frac{AC}{R_1^2} \right) +D \tag{16} \\ 2 = B \log R_2 - \frac{B}{2} E_1\left( \frac{AC}{R_2^2} \right) +D \tag{17} \end{align} $$
上式から$D$を消去する。
$$ 2 = B \log \frac{R_2}{R_1} - \frac{B}{2} \left[ E_1\left( \frac{AC}{R_2^2} \right) - E_1\left(\frac{AC}{R_1^2} \right) \right] \tag{18} $$
これは $C$に関する非線形方程式になっており反復計算により$C$を求める。 $C$の値がきまれば、上記の(16)式から$D$を計算することができる。 今回の解析モデルでは以下のようになった。
$$ C = 0.01637 \\ D = 49.02304 $$
圧力は(7)式を使い、$u_\theta(r)$を含む式を$r$方向に積分することで得られる。 なおここでは$p(R1)=0$とした。
$$ p(r) = \int_{R_1}^{r}\frac{\rho u_\theta^2}{r}dr=\int_{R_1}^{r}\rho r \omega^2dr \tag{19} $$
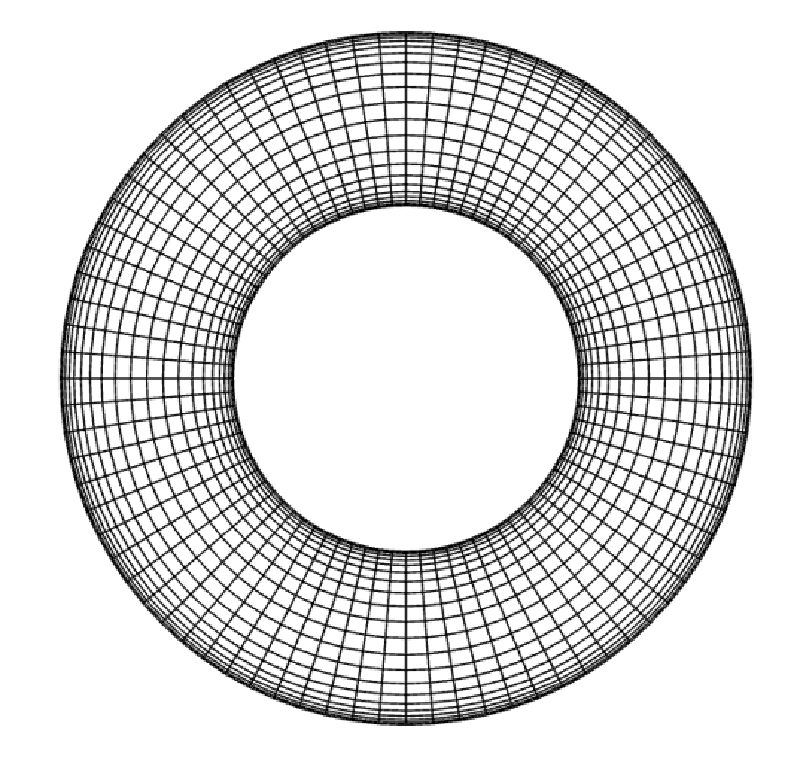
解析モデル
fluentを使い解析を行った。メッシュ分割を以下に示す。
メッシュ
物性値
解析に使用した物性値は前項で示した値と同じである。
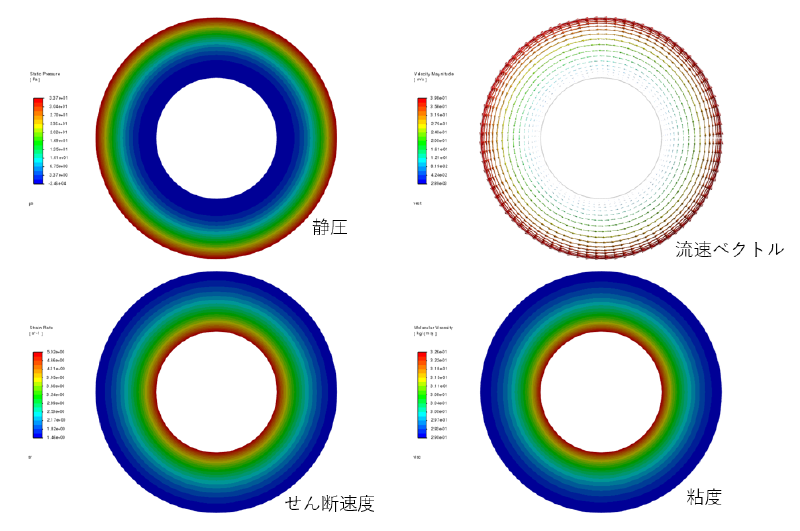
解析結果
いくつかの計算結果図を示す。
ringモデルの結果
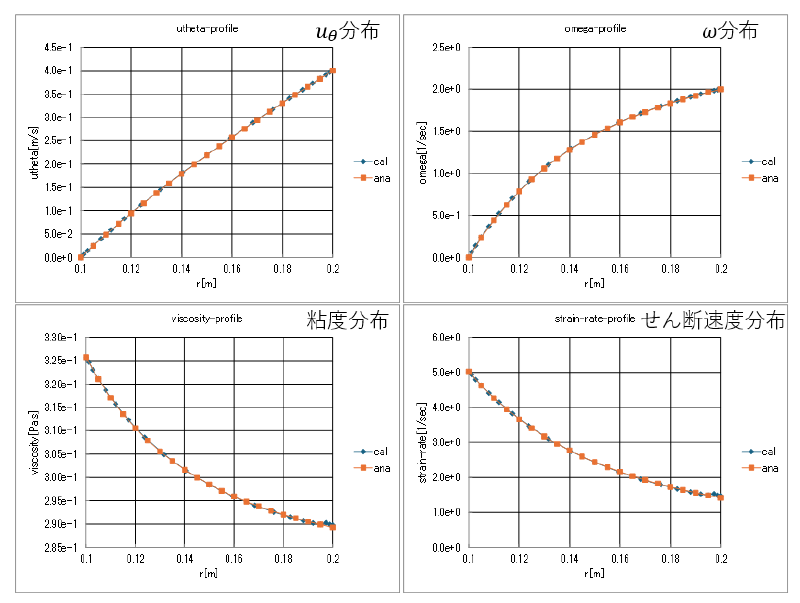
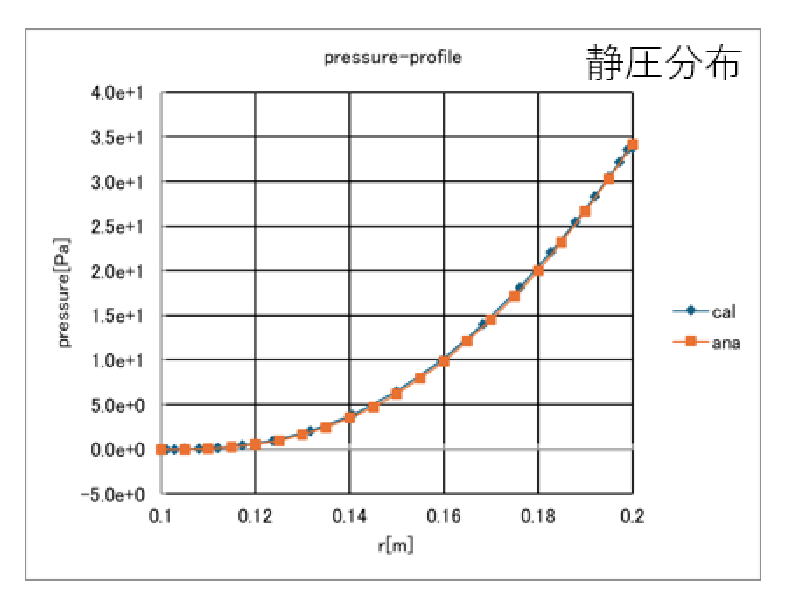
検査線上の物理量分布は以下のようになった。 図中に計算値と理論値を表示しているが両者はよく一致していることがわかる。
xyplot-ring
xyplot-ring2
理論値の計算に使用したプログラム
積分定数$C,D$を求めるjuliaプログラムを以下に示す（calcd.jl)。
using SpecialFunctions
using Roots
A = 0.2
B = 18
R1 = 0.1 # inner radius
R2 = 0.2 # outer radius
angvel = 2 # angular velocity
init = 0.02 # initial guess
err(C) = B*(log(R2/R1)-0.5*(expint(A*C/R2^2)-expint(A*C/R1^2)))-angvel
C = find_zero(err,init)
D = -B*(log(R1)-0.5*expint(A*C/R1^2))
println("$angvel $C $D")
$r$方向の物理量を計算するjuliaプログラムを以下に示す（theory.jl)。
using SpecialFunctions
using QuadGK
r1 = 0.1 # inner radius
r2 = 0.2 # outer radius
A = 0.2
B = 18
C = 0.01636910800571221
D = 49.023042414721075
rho = 1000 # [kg/m^3]
n = 20
dr = (r2-r1)/n
omega(r) = B*(log(r)-0.5*expint(A*C/r^2))+D
omegadot(r) = B/r*(1-exp(-A*C/r^2))
println("radius[m] strain_rate[1/s] viscosity[Pa.s] utheta[m/s] omega[1/s] static_pressure[Pa]")
for i in 0:n
r = r1 + dr*i
omg = omega(r)
ut = r*omg
sr = r*omegadot(r)
visc = log(B/(B-sr))/(sr*A);
ps, error = quadgk(x -> rho*x*omega(x)^2 , r1, r)
println("$r $sr $visc $ut $omg $ps")
end
注意点
fluentの解析を行う際の注意点として、ダイラタント流体の解析を行う場合には、 収束判定値を適切に設定しておくことが必要である。
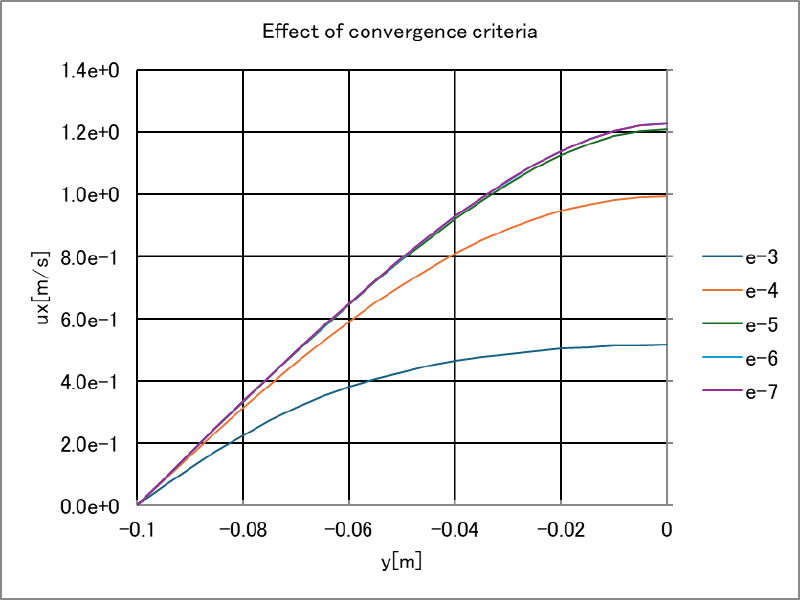
以下に示す図はcase-dp15において、収束判定基準を1e-3（デフォルト）から1e-7まで変化させた場合の流速$u_x$の分布である。
このケースではデフォルトの収束判定基準は不適切であり、3～4桁程度下げておく必要があることがわかる。
convergence
まとめ
ダイラタント流体を対象として、特定の粘度式を使い、簡単な流路形状の場合の理論解を導いた。
またfluentで計算を行い、理論解と計算結果が一致していることが分かった。
弊社の解析事例
弊社の流体解析事例については、下記のリンクからご覧ください．