ピトー管の原理

By M.Sato

概要

ピトー管（Pitot tube）は、流体（主に空気）の速度を測定するための重要な装置で、特に航空機の空気速度（対気速度）測定などに広く使われている。

ここでは軸対称モデルを使い、ピトー管のシミュレーションを行ってみた。

一般的にベルヌイの式に基づき流速を推定するが、 流速が大きくなり流体の圧縮性の効果が顕著な場合、 等エントロピー関係式に基づき流速を推定するのが望ましいことが分かった。

ピトー管の原理

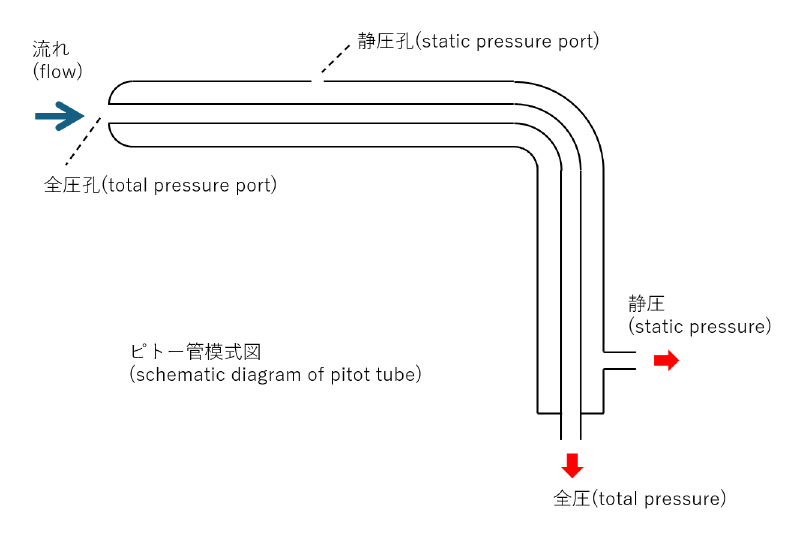
ピトー管は流速を測定する装置であり、その内部構造は下図のようになっている。

ピトー管には$2$つの開口部がある。

  • 静圧口：側面に開いており静圧を測定
  • 全圧口：ピトー管先端で流れに正対するように配置し、全圧を測定

得られた静圧と全圧から流速を推定する仕組みになっている。

principal

次に静圧と全圧から流速を計算する原理について記述する。

流体が流管の中を流れているとする。

位置1と位置2の間の流体のエネルギーの保存式は以下のようになる。

流管

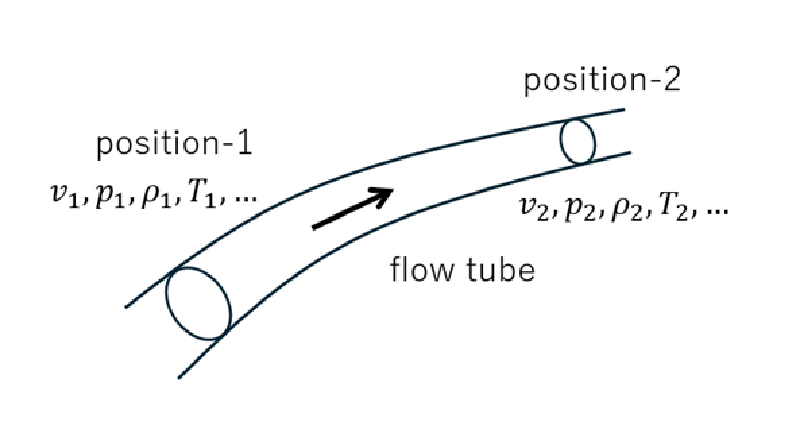
ここで、$v$は流速、$p$は圧力、$\rho$は密度、$T$は温度である。

  • 非圧縮性流体の場合

$$ \begin{align} p_1 + \frac{1}{2} \rho v_1^2 &= p_2 + \frac{1}{2} \rho v_2^2 \end{align} $$

密度は一定なので添字なしの$\rho$で表している。 位置2において流速がゼロ（よどみ点）として添字"$0$“で表し、添字$1$を省略すると次式が得られる。

$$ \begin{align} & p + \frac{1}{2} \rho v^2 = p_0 \ & v = \sqrt{ \frac{2(p_0-p)}{\rho}} \end{align} $$

$p$が静圧、$p_0$が全圧を表しており、これがベルヌイの式に基づいて流速を推定する方法である。

  • (亜音速)圧縮性流体の場合

この場合、温度、密度などが流管の位置によって変化するためベルヌイの式を使うのは不適切である。

流体の状態が等エントロピーで推移する場合、次式で流体エネルギーの保存を記述することができる。

$$ \begin{align} \rho_1 e_1 + p_1 + \frac{1}{2} \rho_1 v_1^2 &= \rho_2 e_2 + p_2 + \frac{1}{2} \rho_2 v_2^2 \end{align} $$

ここで$e$は単位質量あたりの流体の内部エネルギー量であり、 $e=c_vT$と近似される（$c_v$は定積比熱、$T$は絶対温度）。

位置2において流速がゼロ（よどみ点）として添字”$0$“で表し、添字$1$を省略すると、最終的に以下の等エントロピ関係式が得られる。

$$ \begin{align} \frac{p_0}{p} &= \left( 1+ \frac{\gamma-1}{2} M^2\right)^{\frac{\gamma}{\gamma-1}} \\ M^2 &= \frac{2}{\gamma-1}\left[ \left( \frac{p_0}{p} \right)^{\frac{\gamma-1}{\gamma}} -1 \right] \\ v^2 &= a^2 M^2 = \frac{a_0^2 M^2}{1+ \frac{\gamma-1}{2}M^2} \end{align} $$

ここで$a$は音速、$M=v/a$はマッハ数であり、添字$0$は淀み点における物理量を表す。

(6)式を使い、静圧、全圧に基づきマッハ数を求め、(7)式で流速を計算することができる。 (7)式には音速$a$、あるいは$a_0$が必要であるが、これらは測定された温度から計算される（$a=\sqrt{\gamma R T}$）。 静圧口温度の場合$a$、全圧口温度の場合、$a_0$となる。

解析モデル

Ansys Fluentを使い解析を行ってみた。

解析モデルを以下に示す。解析領域は軸対称とした。

流体は常温の空気を想定し、風速が $1$m/sから $200$m/s程度まで変化するとした。

なお流体の圧縮性の効果はマッハ数で見積もることができる。常温($300$K)における空気の音速は約$350$m/s程度である。

$$ a = \sqrt{\gamma R T} = \sqrt{1.4 \cdot 287 \cdot 300 } = 347 [m/s] $$

ここで$\gamma$は比熱比、$R$は気体定数、$T$は絶対温度である。

これより風速$200$m/s時におけるマッハ数は $200/347 = 0.576$ 程度となる。

一般的にはマッハ数が$0.3$以上の場合は圧縮性流体として計算を行うことが必要である。

今回の計算では、高マッハ数の流れにおいて圧縮性を考慮する場合、しない場合で推定流速値に どの程度に差が生じるかを調べてみた。

ピトー管の全圧口は直径 $4$[mm]とし、またピトー管先端から$100$mm下流の側面に幅$3$mmの静圧口があるとした。

また流れは乱流状態と考えられることから、$k\omega\text{-}SST$乱流モデルを使用した。

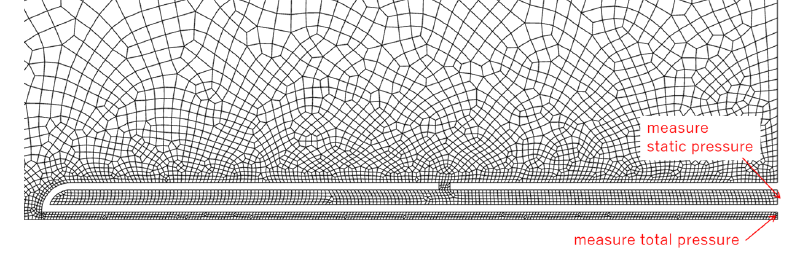
流体密度が、非圧縮性の場合と圧縮性の場合の二種類の計算を行うため、流入境界条件を下図に示すように設定した（これは流入速度$100$[m/s]の場合）。

モデル

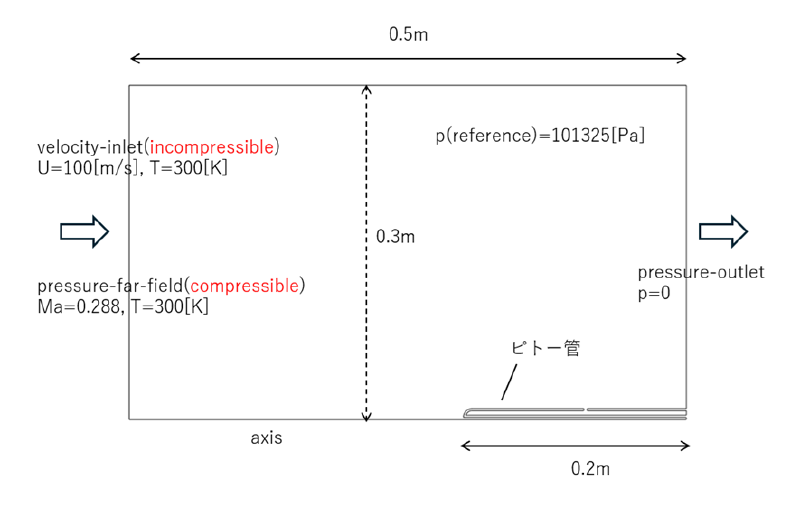
メッシュ分割

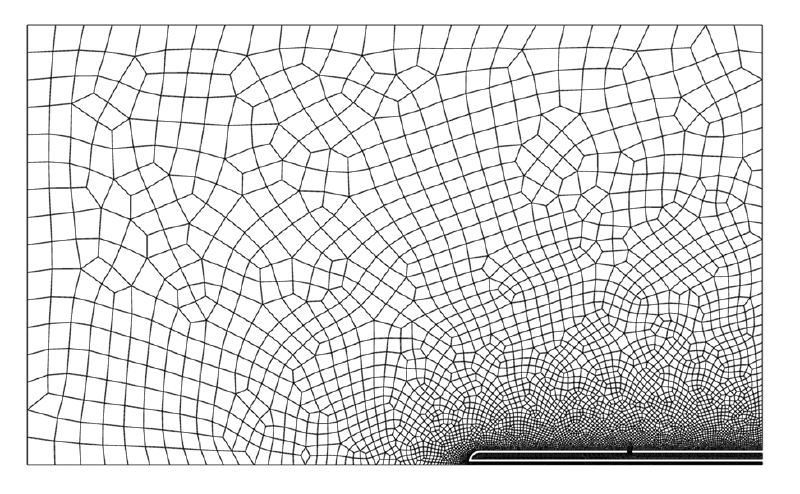
解析に使用したメッシュ分割図を示す。

メッシュ 全体メッシュ図

メッシュ拡大 ピトー管付近の拡大図（図中に圧力検査点の位置を示す）

物性値

流体は常温の空気とした。 流体密度が一定値の場合（非圧縮性）と理想気体（圧縮性）の場合の２つのケースを想定して計算を行ってみた。

以下に示す物性値は、$\rho$は密度、$\mu$は粘度、$\lambda$は熱伝導率、$c_p$は定圧比熱である。

  • 非圧縮性流体解析

$$ \begin{align} \rho &= 1.225 [kg/m^3] \notag \\ \mu &= 1.7894\times 10^{-5} [Pa.s] \notag \end{align} $$

  • 圧縮性流体解析

このケースでは温度も含めて解析を行うことになるため熱物性値が必要である。

$$ \begin{align} \rho &= p/RT \notag \\ \mu &= 1.7894\times 10^{-5} [Pa.s] \notag \\ \lambda &= 0.0242 [W/m/K] \notag \\ c_p &= 1006.43 [J/kg/K] \notag \end{align} $$

解析結果

非圧縮性流体解析

流入速度(vin)を変えて$8$種類の計算を行った$（vin=1,2,5,10,20,50,100,200[m/s]）$。

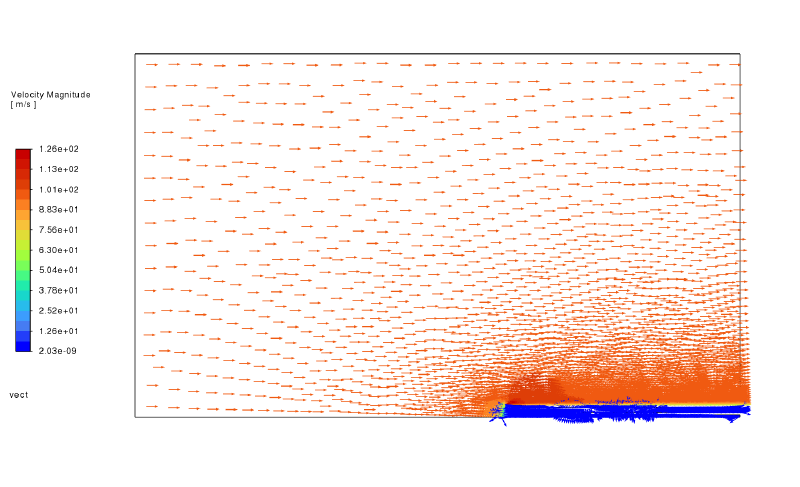
以下に静圧コンター、流速ベクトルの結果図を示す。これらは流入境界での流速が$100$m/sのケースである。

v100-pres-inco 静圧コンター（注：基準圧=$101325$[Pa]とした時のゲージ圧）

v100-vect-inco 流速ベクトル

圧縮性流体解析

流入速度を変えて$4$種類の計算を行った$（vin=20,50,100,200[m/s]）$。

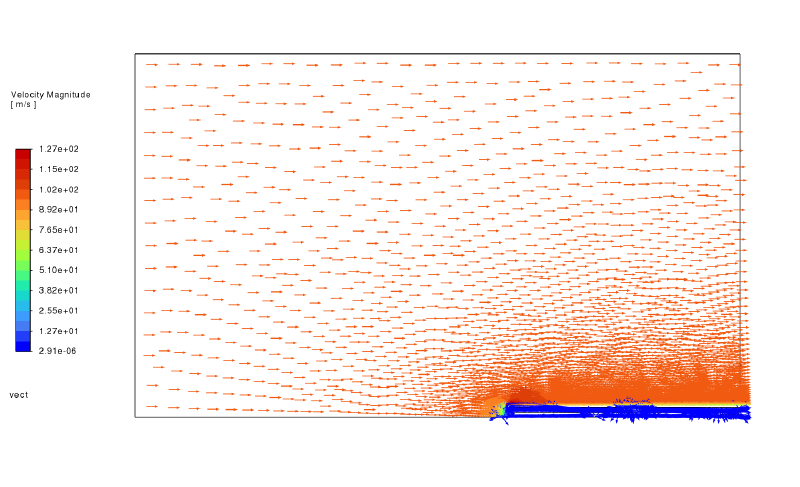
以下に静圧コンター、流速ベクトルの結果図を示す。これらは流入境界での流速が$100$m/sのケースである。

v100-pres-comp 静圧コンター（注：基準圧=101325[Pa]とした時のゲージ圧）

v100-vect-comp 流速ベクトル

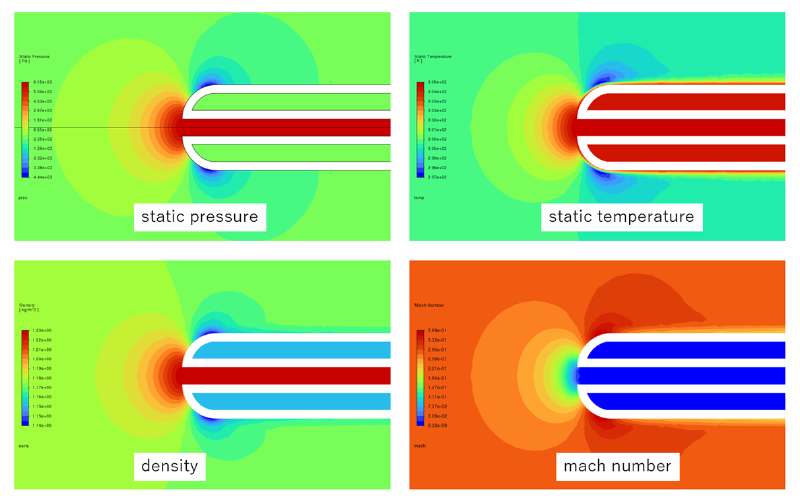v100-comp ノズル先端付近の拡大図（静圧、静温度、密度、マッハ数コンター）

推定された流速値

計算では流入速度を境界条件として指定した。

ピトー管内部の静圧測定面および全圧測定面において圧力値を求めた。 その後流速の推定式に基づき推定を行った。

以下に非圧縮性流体解析と圧縮性流体解析の二種類の結果を示す。

非圧縮性流体解析

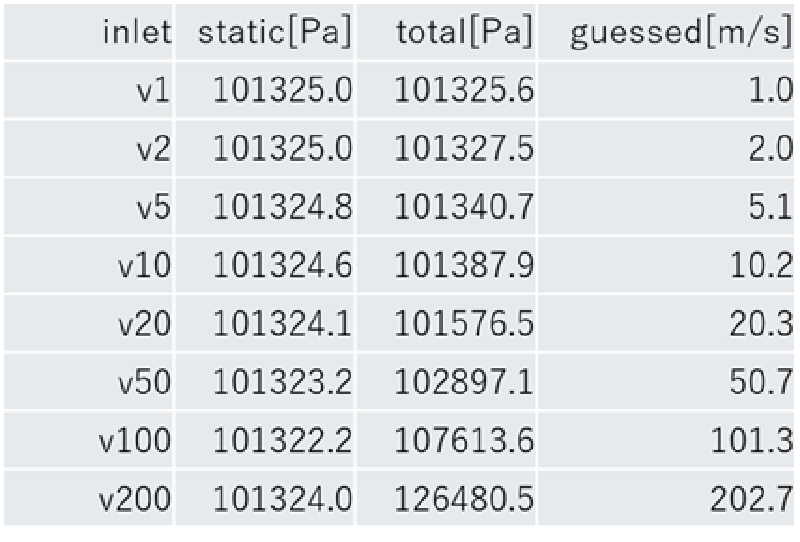
table-inco

表中の inletは流入速度、staticは検査点静圧、totalは検査点全圧、guessedは推定流速値を示す。 これらのケースは非圧縮性流体の仮定に基づき、(3)式で流速を推定した。

推定値は流入速度とほぼ一致していることが分かった。

なお流速が200[m/s]程度になると、本来は圧縮性の効果が生じることになるが、 ここでは非圧縮性流体の前提で解析を行っており、ベルヌイの式を使ってほぼ正しい流速値が推定されていることがわかる。

圧縮性流体解析

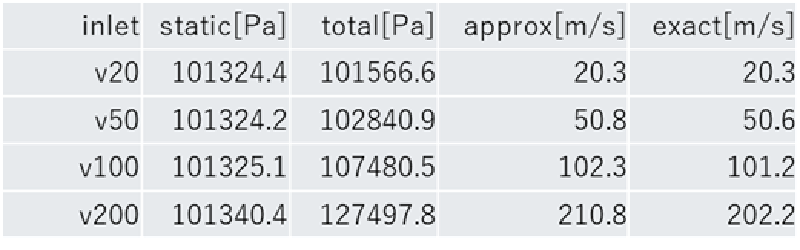
table-comp

表中のinlet, static, total の意味は非圧縮性流体解析の結果と同じである。 approxは、流速を上述の(3)式（非圧縮性流体）を使い推定したもの、exactは上述の(7)式（圧縮性流体）から推定したものである。

流速が大きくなり圧縮性の効果が顕著になるとベルヌイの式を使った推定流速は誤差が大きくなっていることがわかる。

参考までに圧縮性流体の流速推定に使用したjuliaコードを示す。


data = []

open("pres-comp.dat", "r") do io
    for (i, line) in enumerate(eachline(io))
        if i == 1
            continue  # ヘッダー行をスキップ
        end
        tokens = split(line)
        push!(data, parse.(Float64, tokens[2:end]))
    end
end

function mach(gamma,ps,pt)
    ratio = pt/ps
    power = (gamma-1)/gamma
    return sqrt( 2.0/(gamma-1.0) * ( ratio^power - 1.0 ) )
end

gamma = 1.4
R = 287
temp = 300
vs2 = gamma*R*temp

labels = [ "v20", "v50", "v100", "v200" ]

for i in 1:4
    label = labels[i]

    ps = data[i][3]  # static pressure
    pt = data[i][4]  # total pressure

# approx
    rho = ps/(R*temp)
    vap = sqrt(2*(pt-ps)/rho)

# exact
    mc = mach(gamma,ps,pt)
    vel2 = vs2*mc^2
    vex = sqrt(vel2)

    println("i=$i  label=$label  vap=$vap  vex=$vex")
end

まとめ

ピトー管を対象として流速の測定をシミュレーションで再現してみた。

流速が大きい場合（すなわちマッハ数が大きい）には、流体密度が大きく変化するため、 非圧縮性流体で使われるベルヌイの式は不適切となり、等エントロピー関係式を使うのが望ましいことが分かった。

なお、ここでは示していないがさらに流速が大きくなり超音速流れになる場合には、 衝撃波前後の圧力を使い、別式を使って計算することが必要である。

弊社の解析事例

弊社の流体解析事例については、下記のリンクからご覧ください．

👉 解析事例のご紹介 FLUENT

👉 流体解析 実績及び事例