異方性多孔質体の計算

By M.Sato

April 1, 2025

概要

流体中に置かれた多孔質体を通過する流れ場を計算したい場合がある。

多孔質体とは、ミクロ的に見ると固相領域と流体領域が混在した材料であり、一般的には流れ計算を行う際には、多孔質体の流動抵抗を流体に作用する等価な体積力としてモデル化して計算することが多い。

Ansys Fluentでもこの手法を使った多孔質の解析が可能である。

ここでは、多孔質体に作用する体積力項をユーザ定義関数で指定し、任意の多孔質体形状に対して等方性、異方性の多孔質体モデルが計算可能であることを示す。

多孔質体を含む解析

流体中に置かれた多孔質体を計算に考慮する場合、流体に多孔質体による体積力が作用しているものとしてモデル化されることになる。

fluentでは次式で表される抵抗表現式を使っている。

$$ \begin{align} S_i = -\left( \sum_{j=1}^3 D_{ij} \mu v_j + \sum_{j=1}^3 C_{ij} \frac{1}{2} \rho |v| v_j \right) \notag \end{align} $$

ここで$S_i$は$i$番目の運動量のソース項、$v_i$は$i$番目の流速、$|v|$は速度の大きさである。 $D_{ij},C_{ij}$は経験的に決められる抵抗係数テンソルである。この運動量シンクはセル内の流体速度（あるいは速度の二乗）に比例する圧力損失(体積力)を発生させる。

上式をベクトル形式で表すと以下のようになる

$$ \begin{align} \mathbf{S} &= -\left( \mu \mathbf{D} \mathbf{v} + \frac{1}{2} \rho |\mathbf{v}| \mathbf{C} \mathbf{v} \right) \notag \\ &= -\left( \mu \mathbf{D} + \frac{1}{2} \rho |\mathbf{v}| \mathbf{C} \right) \mathbf{v} \notag \\ & \equiv -\mathbf{A}\mathbf{v} \notag \end{align} $$

fluentではこれらの多孔質体モデルは標準で組み込まれており、 GUI画面から多孔質の設定を行うことが可能である。

例えば二次元モデルの場合以下のような設定を行う。

抵抗係数テンソル($\mathbf{D},\mathbf{C}$)は直交異方性として主軸方向の抵抗係数と主軸の方向ベクトルを指定する。

この指定方法では多孔質体は、主軸方向は領域に渡って一定である場合に限定され、また完全異方性の指定を行うことはできない。

一方で、この標準機能を使わずに自作のユーザ定義関数(UDF)を使うことも可能である。

UDFを使う場合、抵抗特性を、座標値や流動特性値に応じて任意に指定することが可能であり、完全異方性の指定も可能である。

ここでは二次元モデルを対象にして極座標系に基づいて異方性の抵抗係数を指定する方法を説明する。

まず座標系の回転によってベクトルの成分がどのように変換されるのかを示す。

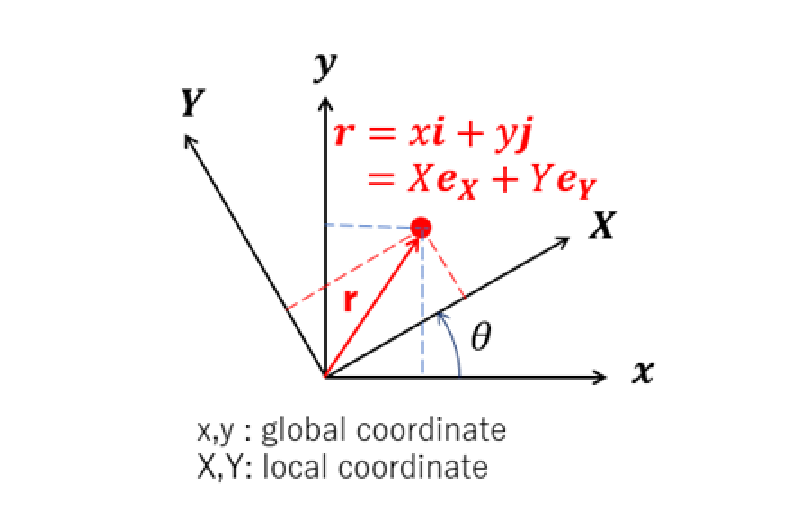
全体座標系と局所座標系でのベクトル成分の変換は次式で表される。

$$ \begin{align} \left( \begin{matrix} X \\ Y \end{matrix} \right) = \left[ \begin{matrix} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{matrix} \right] \left( \begin{matrix} x \\ y \end{matrix} \right) \notag \end{align} $$

ここで座標値変換マトリックスを$\mathbf{P}$と表すことにする。 $\mathbf{P}$は直交行列であり、逆行列は転置行列になる（$\mathbf{P}^{-1}=\mathbf{P}^T$）。

$$ \mathbf{P}= \left[ \begin{matrix} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{matrix} \right] $$

流速ベクトル$\mathbf{v}$、多孔質体による体積力ベクトル$\mathbf{S}$は以下の座標変換で表される。ここで添字$\mathbf{G},\mathbf{L}$はそれぞれ全体座標系、局所座標系を表している。

$$ \mathbf{v_{L}}= \left( \begin{matrix} v_X \\ v_Y \end{matrix} \right) = \mathbf{P} \left( \begin{matrix} v_x \\ v_y \end{matrix} \right) =\mathbf{P} \mathbf{v_{G}} $$

$$ \mathbf{S_{L}}= \left( \begin{matrix} S_X \\ S_Y \end{matrix} \right) = \mathbf{P} \left( \begin{matrix} S_x \\ S_y \end{matrix} \right) =\mathbf{P} \mathbf{S_{G}} $$

次に抵抗係数であるが、局所座標系で表すと体積力と流速には次の関係式が成り立つとする（ここで抵抗係数$\mathbf{A}$は$\mathbf{C},\mathbf{D}$をまとめて表現したものと考えることができる）。

局所座標系は多孔質体の主軸方向を基準にとるものと解釈することにする。 $A_{12}=A_{21}=0$の場合が直交異方性に対応している。

$$ \begin{align} \mathbf{S_{L}}= \left( \begin{matrix} S_X \\ S_Y \end{matrix} \right) = \left[ \begin{matrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{matrix} \right] \left( \begin{matrix} v_X \\ v_Y \end{matrix} \right) = \mathbf{A_{L}} \mathbf{v_{L}} \notag \end{align} $$

上式を使うと全体座標系での多孔質体の抵抗係数テンソル$\mathbf{A_G}$は以下のように変換されることがわかる。

$$ \mathbf{A}_{G} = \mathbf{P}^T \mathbf{A}_L \mathbf{P} $$

解析例

fluentを使った計算例を示す。多孔質体の抵抗特性が極座標系で記述される場合を考える。

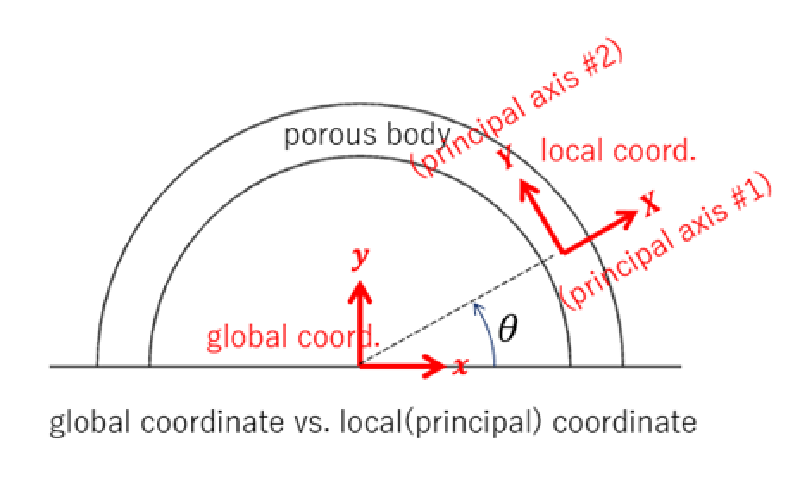
この場合、$\mathbf{A_G}$を具体的に記述すると以下のようになる。

なおここでは簡単のため、$C=\cos\theta,S=\sin\theta$とおいた。

この抵抗係数をUDFに組み込んで流れの様子を調べてみた。

$$ \mathbf{A}_{G} = $$ $$ \left[ \begin{matrix} C^2A_{11}+S^2A_{22}-CS(A_{12}+A_{21}) & CS(A_{11}-A_{22})+C^2A_{12}-S^2A_{21} \\ CS(A_{11}-A_{22})+C^2A_{21}-S^2A_{12} & S^2A_{11}+C^2A_{22}+CS(A_{12}+A_{21}) \end{matrix} \right] $$

以下のケースについて解析を行った。

case	model	resistance	setting
1	1	isotropic(等方性)	GUI
2	1	isotropic(等方性)	UDF
3	1	orthotropic(直交異方性)	UDF
4	1	orthotropic(直交異方性)	UDF
5	2	anisotropic(完全異方性)	UDF

注：GUIは標準の多孔質体設定画面から多孔質特性を指定、 UDFはユーザ定義関数を使って体積力を指定したことを示している

以下にモデルの説明図を示す。これらはいずれも２次元モデルである。

モデル１では平行流れの中にリング状の多孔質体が置かれた場合を想定している。

モデル２は中心にある円形の境界から流入した流体がリング状の多孔質体を通過する場合を想定している。

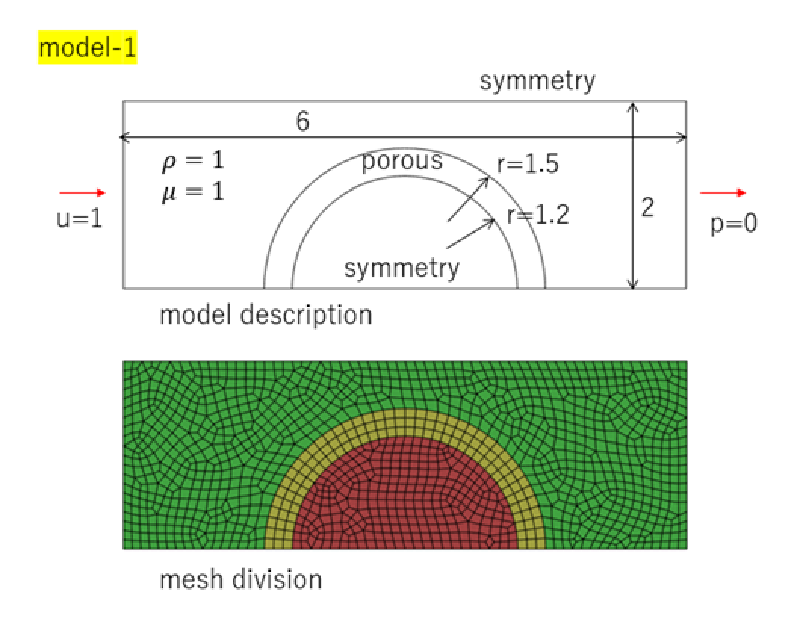
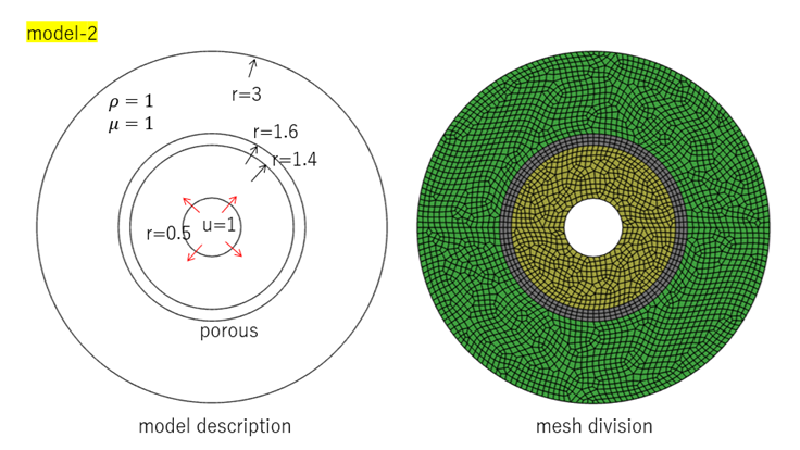
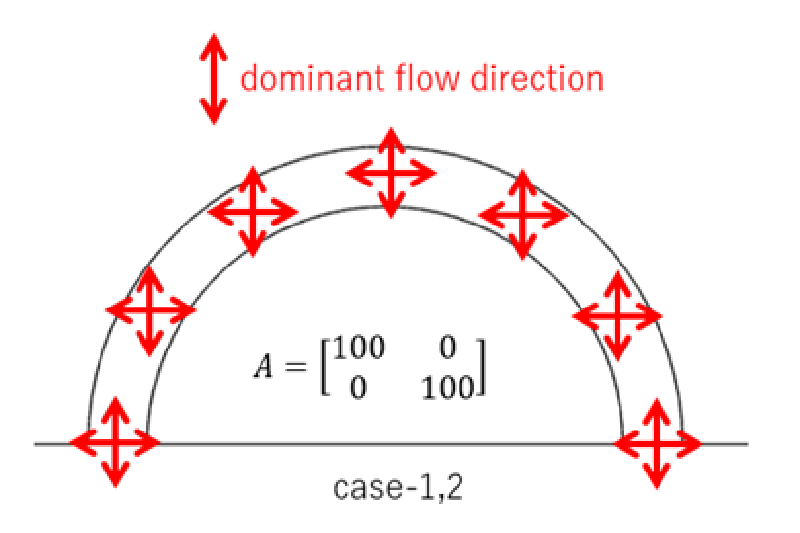
case-1

このケースは等方性の多孔質体を計算した例である。

多孔質体が抵抗となるため流れが多孔質体を避けて流れる傾向がある。

case-1ではGUIの設定を使用した。

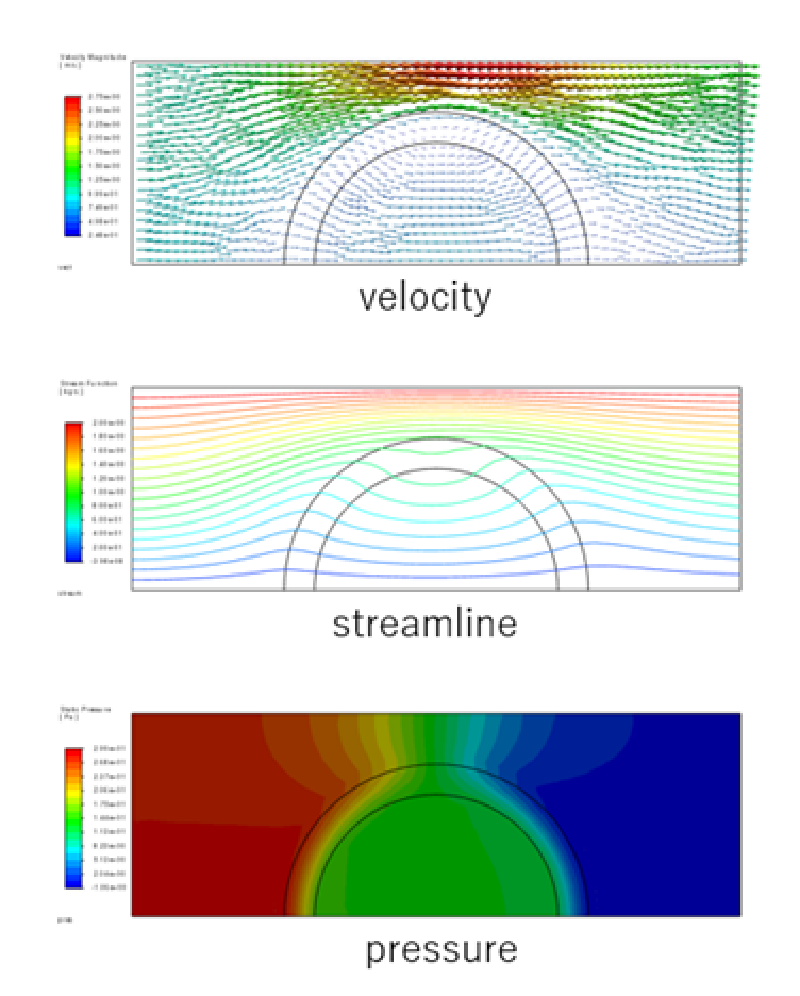
case-2

このケースはcase-1と同じ条件であるがUDFを使って計算したものである。

なお、圧力の離散化指定はPRESTO!にしておく必要がある。

case-1と同じ計算結果になっていることがわかる。

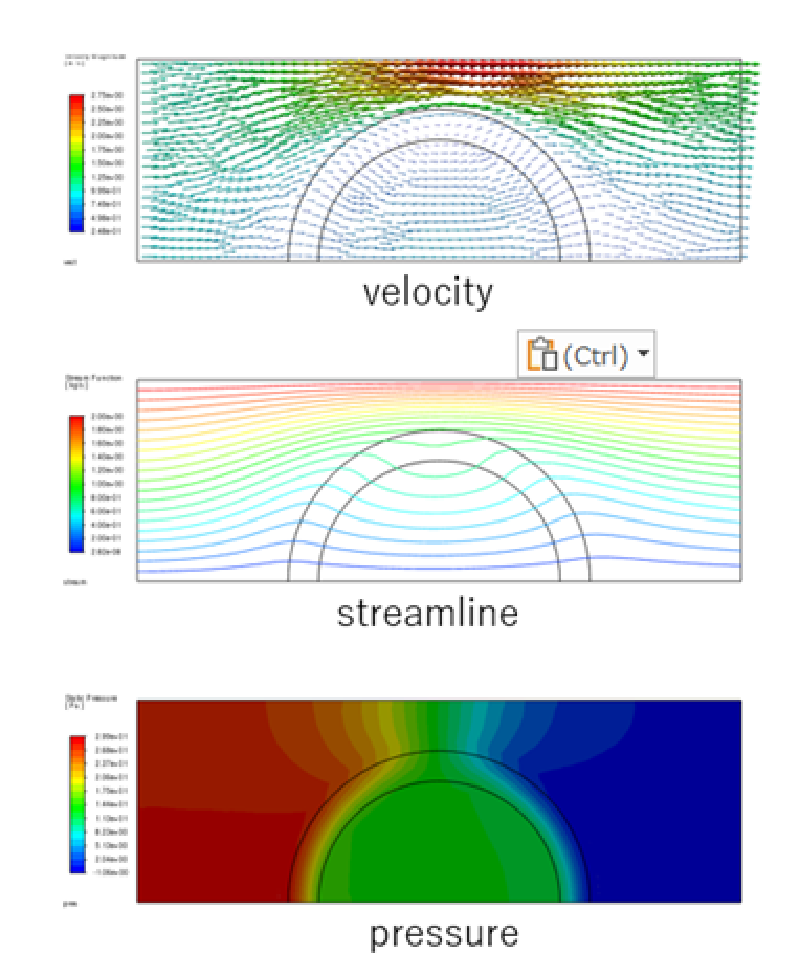
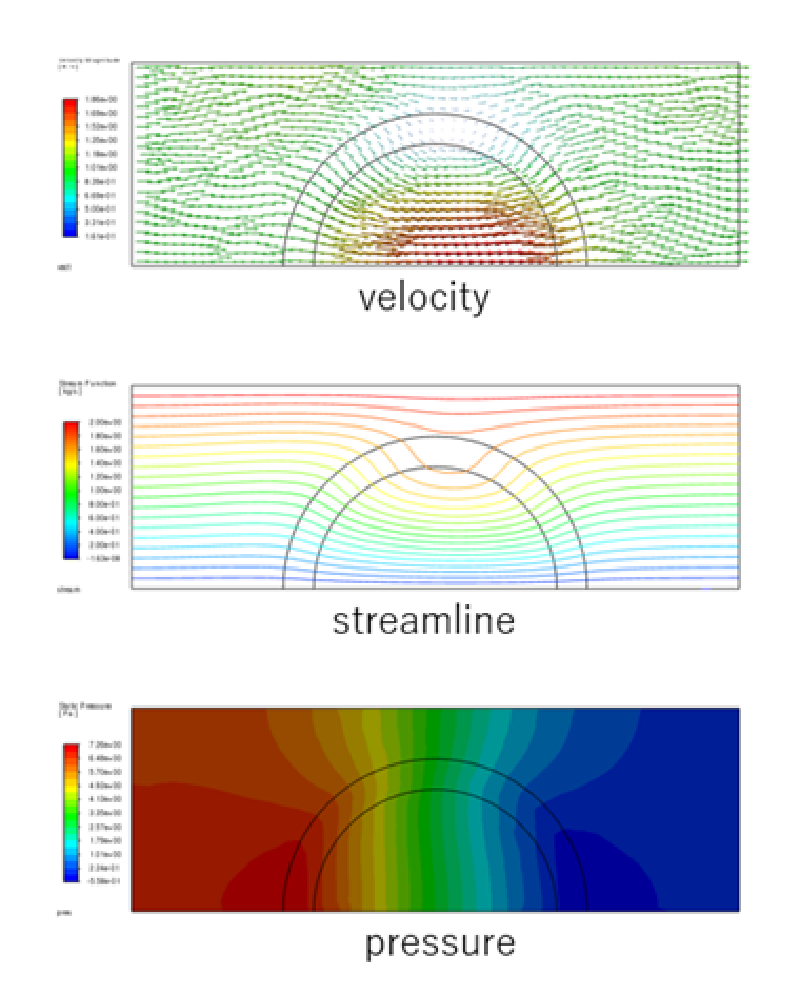
case-3

このケースは主軸#2方向(円周方向)の抵抗を大きくしたケースであり、その結果、主軸#1方向(半径方向)の流れが顕著になる。

計算結果を見ると多孔質体リングの対称面付近で流速が大きくなっていることがわかる。

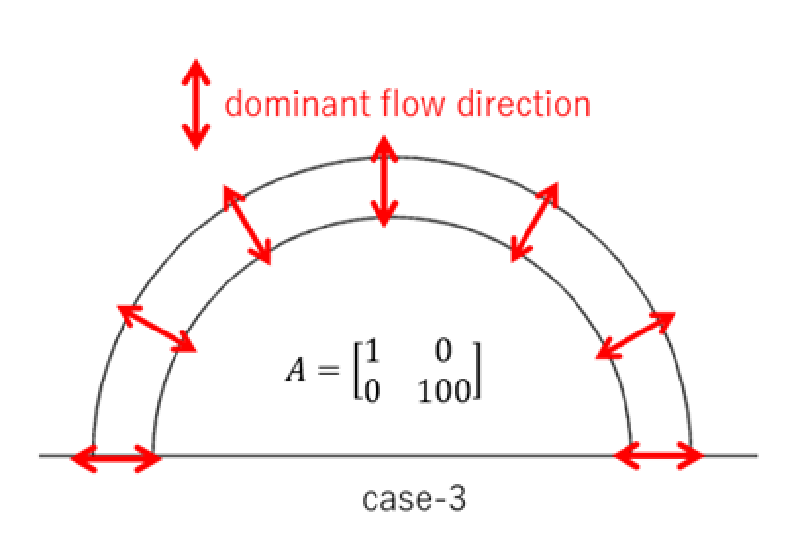
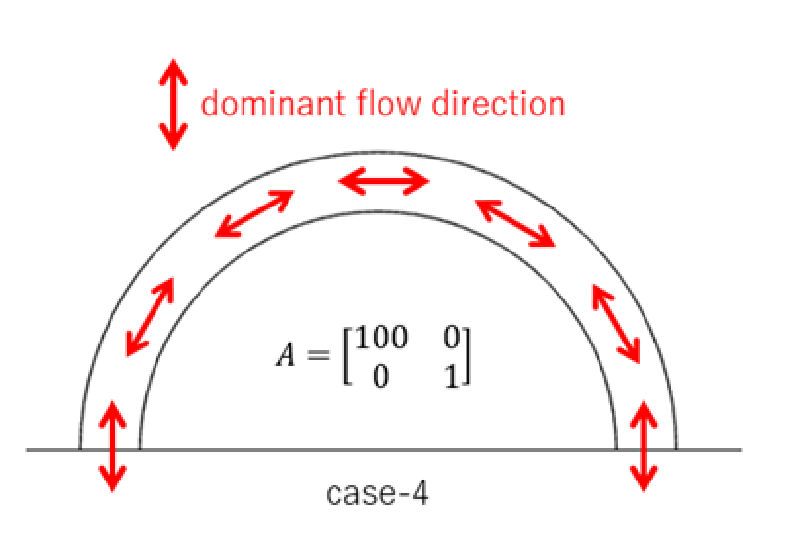
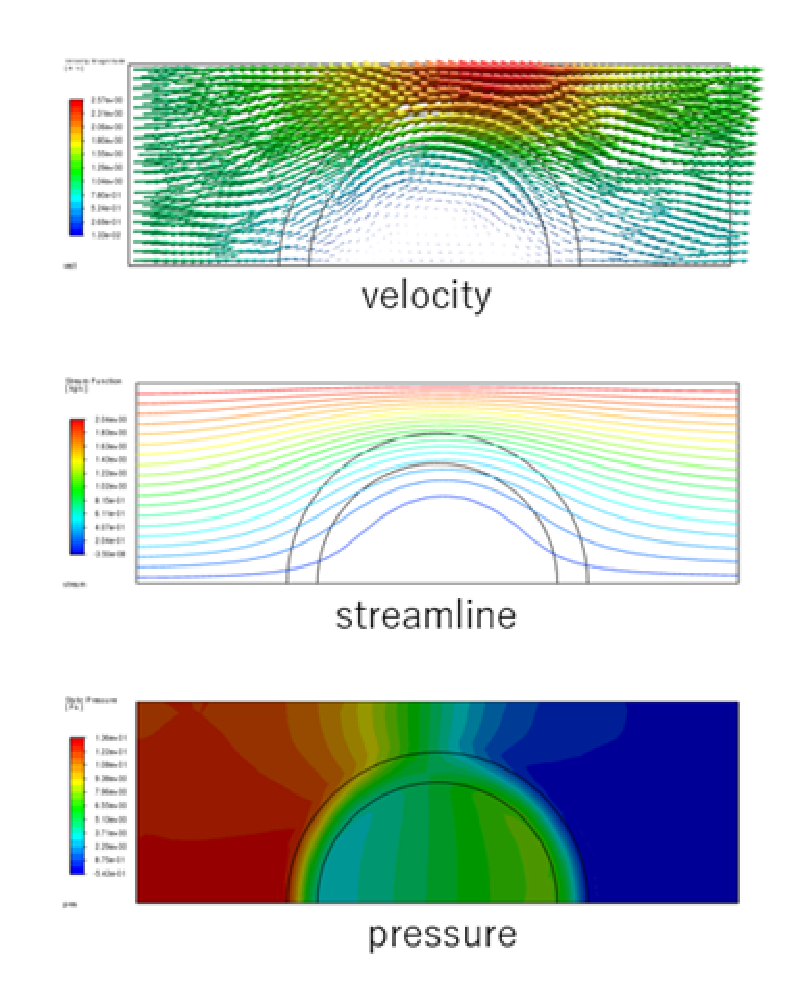
case-4

このケースは主軸#1方向(半径方向)の抵抗を大きくしたケースであり、その結果主軸#2方向(円周方向)の流れが顕著になる。

計算結果を見ると多孔質体リングの対称面付近付近で流速が遅くなり、側面付近で流速が速くなっていることがわかる。

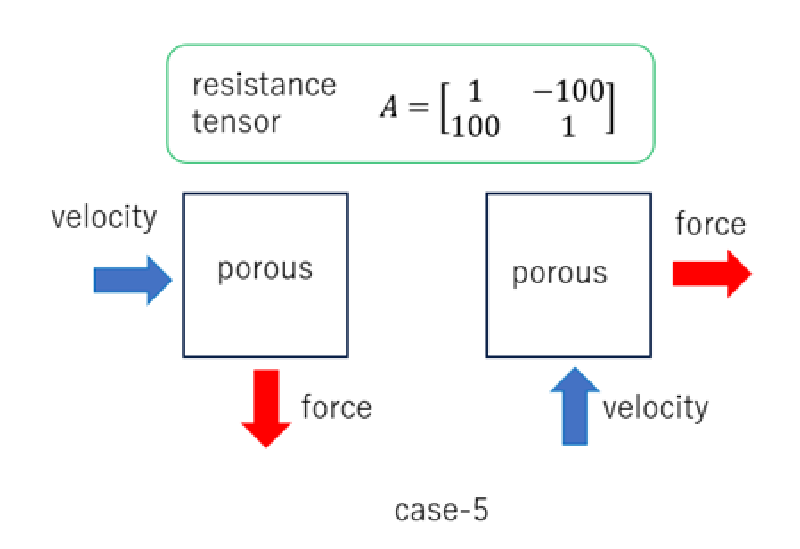
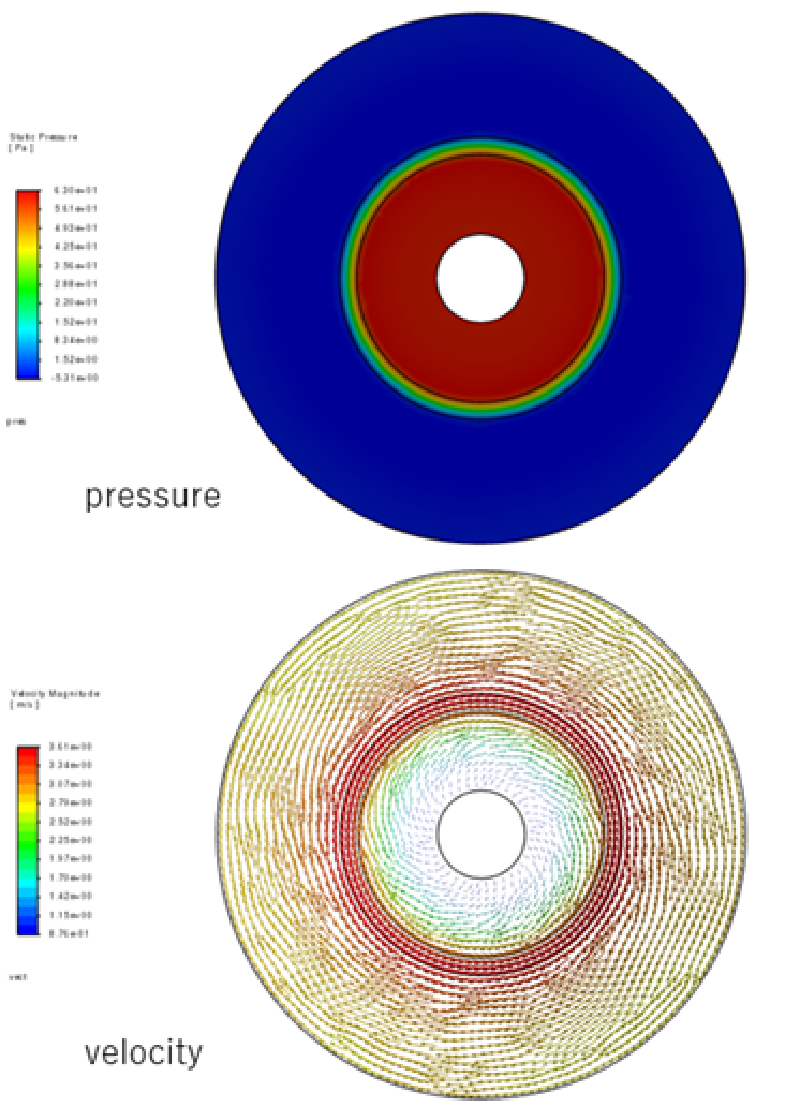
case-5

このケースは完全異方性の多孔質特性を指定した例であり、流速方向と抵抗方向が異なっている。

ここでは流速方向に対して右側に体積力が作用するとした。

計算結果を見ると多孔質体に沿って時計まわりに循環するような流れが生じていることがわかる。

ユーザ定義関数

計算に使用したUDFを示す。

以下の関数をx,y方向の運動量方程式のソース項として指定する。

#include "udf.h"

/* case2: isotropic */
/*
#define A11  100.0
#define A12    0.0
#define A21    0.0
#define A22  100.0
*/

/* case3: orthotropic */

#define A11    1.0
#define A12    0.0
#define A21    0.0
#define A22  100.0


/* case4: orthotropic */
/*
#define A11  100.0
#define A12    0.0
#define A21    0.0
#define A22    1.0
*/

/* case5: anisotropic */
/*
#define  A11     1.0
#define  A12  -100.0
#define  A21   100.0
#define  A22     1.0
*/

/*-----------------------------------------------------------*/
DEFINE_SOURCE(x_source,c,t,dS,eqn)
/*-----------------------------------------------------------*/
{
   real x[ND_ND];
   real source,cs,sn,rr,d11,d12,d21,d22;

   C_CENTROID(x,c,t);
   rr = sqrt(x[0]*x[0]+x[1]*x[1]);
   cs = x[0]/rr;
   sn = x[1]/rr;

   d11 = cs*cs*A11 + sn*sn*A22 - cs*sn*(A12+A21);
   d12 = cs*sn*(A11-A22) + cs*cs*A12 - sn*sn*A21;
   d21 = cs*sn*(A11-A22) + cs*cs*A21 - sn*sn*A12;
   d22 = sn*sn*A11 + cs*cs*A22 + cs*sn*(A12+A21);

   source = - ( C_MU_L(c,t)*( +d11*C_U(c,t) 
                              +d12*C_V(c,t) ) );

   dS[eqn] = - ( C_MU_L(c,t)*d11 );

   return source;
}


/*-----------------------------------------------------------*/
DEFINE_SOURCE(y_source,c,t,dS,eqn)
/*-----------------------------------------------------------*/
{
   real x[ND_ND];
   real source,cs,sn,rr,d11,d12,d21,d22;

   C_CENTROID(x,c,t);
   rr = sqrt(x[0]*x[0]+x[1]*x[1]);
   cs = x[0]/rr;
   sn = x[1]/rr;

   d11 = cs*cs*A11 + sn*sn*A22 - cs*sn*(A12+A21);
   d12 = cs*sn*(A11-A22) + cs*cs*A12 - sn*sn*A21;
   d21 = cs*sn*(A11-A22) + cs*cs*A21 - sn*sn*A12;
   d22 = sn*sn*A11 + cs*cs*A22 + cs*sn*(A12+A21);

   source = - ( C_MU_L(c,t)*( +d21*C_U(c,t) 
                              +d22*C_V(c,t) ) );

   dS[eqn] = - ( C_MU_L(c,t)*d22 );

   return source;
}

まとめ

多孔質を通過する流れを計算する際に、ユーザ定義関数を使うことになり汎用的な設定を行えることを示した。

ここでは抵抗特性は一定値としているが、抵抗係数を流れ場、温度場などの関数とすることも可能である。

また多孔質体の形状を局所(主軸)座標系で記述可能であれば任意の複雑形状に対しても適用可能である。

なお、多孔質体の流動抵抗は流れ方向の逆方向に生じる(すなわち、直交異方性)ものが普通であり、完全異方性となるような流れ場は現実にはあまり存在しないと思われる。

弊社の解析事例

弊社の流体解析事例については、下記のリンクからご覧ください．

👉 解析事例のご紹介 FLUENT

👉 流体解析実績及び事例