実在気体モデルの効果

By M.Sato

January 7, 2025

概要

気体を対象として流体現象を調べる場合、圧力が極めて高い、あるいは温度が極めて低いような条件では、気体は理想気体として扱うことが不適切となる。

これは、

(1)気体分子間に作用する引力の効果
(2)全容積に占める気体分子自体の体積

の影響が無視できなくなるためである。

このような条件下で解析を行うためには、実在気体モデルを使い、気体の状態方程式を正しく表現することが必要である。

ここでは、水素ガスを対象としていくつかの実在気体モデルと理想気体モデルの圧力-密度関係の比較を行った。

また衝撃波管の解析を行い実在気体モデルと理想気体モデルの影響を調べた。

状態方程式

気体の圧力と温度と体積の関係は状態方程式によって記述される。 Ansys Fluentでは実在気体を計算するために以下の手法が利用できる。

三次状態方程式モデル
NIST実在気体モデル
ユーザ定義関数モデル

三次状態方程式モデルにおける圧力$P$の一般形は次式で表される。

$$ \begin{align} P &= \frac{RT}{V-b+c} - \frac{\alpha}{V^2+\delta V + \epsilon} \notag \end{align} $$

ここで、$P$：絶対圧[Pa]、$V$：比モル体積[$m^3/kmol$]、$T$：温度[K]、 $R$：一般気体定数[J/kmol/K]である。

係数$a,b,c,\delta$および$\epsilon$は、臨界温度$T_c$，臨界圧力$P_c$，偏心係数$\omega$，および臨界比体積$V_c$の関数として与えられる。

引力係数$\alpha$も温度に依存するが，この依存関係は状態方程式モデルごとに異なり，一般には$\alpha=\alpha(T)$と表される。

ここではfluentで利用可能な、Redlich-Kwongモデル、Soave-Redlich-Kwongモデル、 Peng-Robinsonモデル、Aungier-Redlich-Kwongモデルを対象として物性値の特性を調べた。

また比較のため、Van-Der-Waalsモデル、理想気体モデルの特性も調べた。

各モデルの状態方程式を以下に示す。

Redlich-Kwongモデル(RK)

$$ \begin{align} &P = \frac{RT}{V-b+c} - \frac{\alpha}{V^2+\delta V + \epsilon} \notag \\ &\alpha(T) = \frac{\alpha_0}{(T/T_c)^{0.5}} \notag \\ &\alpha_0 = \frac{0.42747 R^2 T_c^2}{P_c} \notag \\ &b = \frac{0.08664 R T_c}{P_c} \notag \\ &\delta = b \notag \\ &c = \epsilon = 0 \notag \end{align} $$

Soave-Redlich-Kwongモデル(SRK)

$$ \begin{align} &P = \frac{RT}{V-b+c} - \frac{\alpha}{V^2+\delta V + \epsilon} \notag \\ &\alpha(T) = \alpha_0 \left[ 1+n\left(1-\left(\frac{T}{T_c}\right)^{0.5} \right) \right]^2 \notag \\ &\alpha_0 = \frac{0.42747 R^2 T_c^2}{P_c} \notag \\ &b = \frac{0.08664 R T_c}{P_c} \notag \\ &n = 0.48 + 1.574\omega -0.176\omega^2 \notag \\ &\delta = b \notag \\ &c = \epsilon = 0 \notag \end{align} $$

Peng-Robinsonモデル(PR)

$$ \begin{align} &P = \frac{RT}{Vb+c} - \frac{\alpha}{V^2+\delta V + \epsilon} \notag \\ &\alpha(T) = \alpha_0 \left[ 1+n\left(1-\left(\frac{T}{T_c}\right)^{0.5} \right) \right]^2 \notag \\ &\alpha_0 = \frac{0.45724 R^2 T_c^2}{P_c} \notag \\ &b = \frac{0.07780 R T_c}{P_c} \notag \\ &n = 0.37464 + 1.54226\omega -0.26992\omega^2 \notag \\ &\delta = 2b \notag \\ &c = 0 \notag \\ &\epsilon = -b^2 \notag \end{align} $$

Aungier-Redlich-Kwongモデル(ARK)

$$ \begin{align} &P = \frac{RT}{V-b+c} - \frac{\alpha}{V^2+\delta V + \epsilon} \notag \\ &\alpha(T) = \alpha_0 \left(\frac{T}{T_c}\right)^{-n} \notag \\ &\alpha_0 = \frac{0.42747 R^2 T_c^2}{P_c} \notag \\ &b = \frac{0.08664 R T_c}{P_c} \notag \\ &n = 0.4986 + 1.1735\omega +0.4754\omega^2 \notag \\ &\delta = b \notag \\ &\epsilon = 0 \notag \\ &c = \frac{RT_c}{P_c+\frac{\alpha_0}{V_c(V_c+b)}} + b -V_c \notag \end{align} $$

Ideal-gasモデル(Ideal)

$$ \begin{align} &P = \frac{RT}{V} \notag \end{align} $$

Van-Der-Waalsモデル(VDW)

$$ \begin{align} &P = \frac{RT}{V-b} - \frac{a}{V^2} \notag \end{align} $$

密度の比較

後述するfluentの検証例題 VMFL026では、水素ガスを対象として実在気体モデル（ARK）を適用している。

そこで、ここでは水素ガスを対象として上記の各状態方程式から密度を計算し、各モデルでどの程度の違いがあるのかを調べてみた。

温度を 300[K]とした場合の比モル体積と圧力の関係は下図のようになった。

ファンデルワールス状態方程式(VDW)では、水素ガスに対する係数($a=24.76\times 10^3[Pa\cdot m^6/kmol],b=26.61\times 10^{-3}[m^3/kmol]$)を使用した。

なお図中のNISTは熱物性値データベースNIST Chemistry WebBook, SRD 69から入手した水素物性値である。比モル体積が小さい領域を拡大した図をあわせて示している。

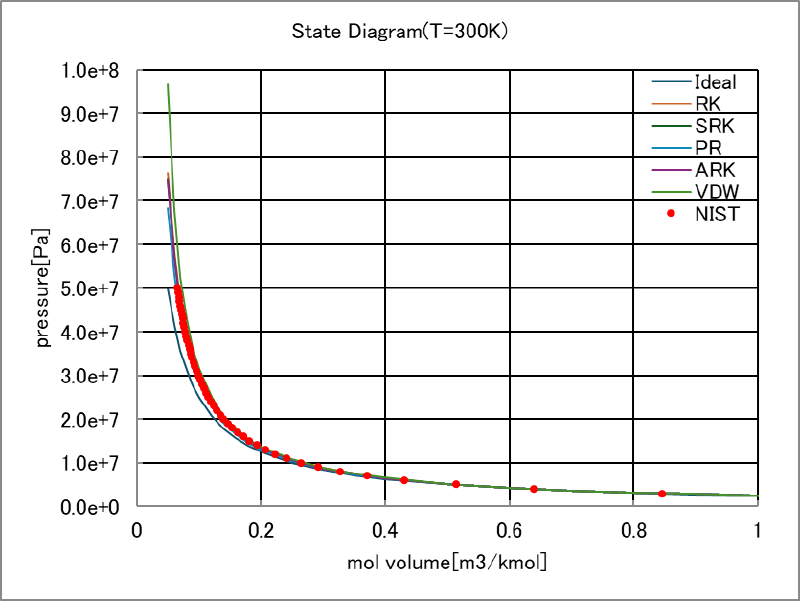
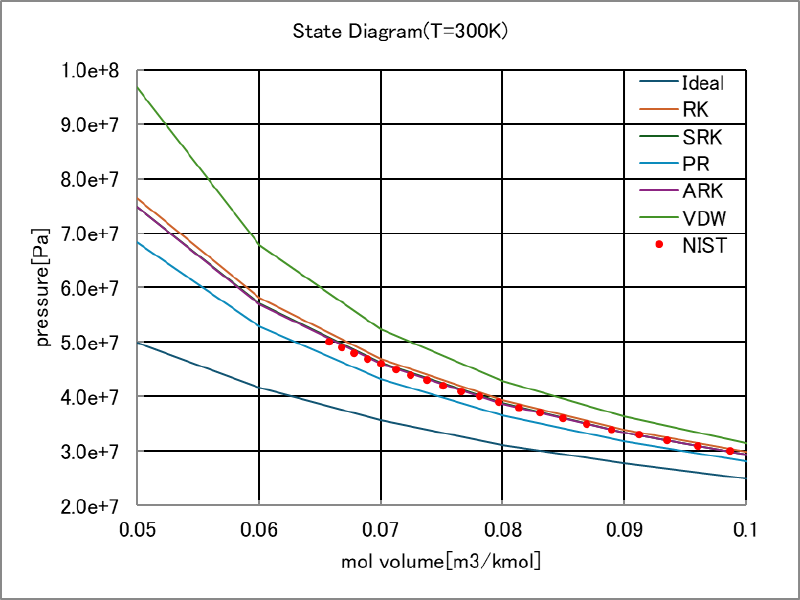
これらの図を見ると、Ideal, VDW, PRは測定値（NISTデータ）とあまり一致していないが、RK,SRK,ARKはほぼ測定値に一致していることがわかる。

次に比モル体積から密度を計算し、圧力と密度の関係としてグラフにした図を示す。（$\rho$=分子量/比モル体積）

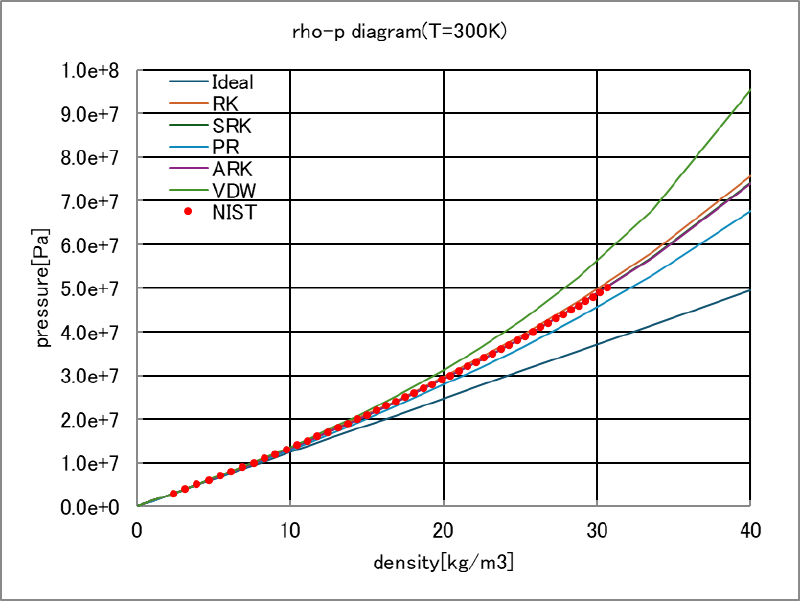
圧力が $5\times10^7[Pa]$では、実在気体密度が約30[kg/m3]であるのに対して、理想気体密度は約40[kg/m3]程度となっており、大きく異なっていることがわかる。

参考までに比モル体積（あるいは密度）と圧力の関係を計算するjuliaプログラムを以下に示す。


abstract type Gases end

struct Ideal <: Gases
    R  # gas constant [J/K/kmol]
    MW # molecular weight [kg/kmol]
end

struct RedlichKwong <: Gases
    R  # gas constant [J/K/kmol]
    MW # molecular weight [kg/kmol]
    Tc # critical temperature [K]
    Pc # critical pressure [Pa]
end

struct SoaveRedlichKwong <: Gases
    R  # gas constant [J/K/kmol]
    MW # molecular weight [kg/kmol]
    Tc # critical temperature [K]
    Pc # critical pressure [Pa]
    Ec # eccentricity coef [-]
end

struct PengRobinson <: Gases
    R  # gas constant [J/K/kmol]
    MW # molecular weight [kg/kmol]
    Tc # critical temperature [K]
    Pc # critical pressure [Pa]
    Ec # eccentricity coef [-]
end

struct AungierRedlichKwong <: Gases
    R  # gas constant [J/K/kmol]
    MW # molecular weight [kg/kmol]
    Tc # critical temperature [K]
    Pc # critical pressure [Pa]
    Vc # critical specific volume [m3/kmol]
    Ec # eccentricity coef [-]
end

struct VanDerWaals <: Gases
    R  # gas constant [J/K/kmol]
    MW # molecular weight [kg/kmol]
    a  # [Pa.m6/kmol2]
    b  # [m3/kmol]
end

#-------------------------------------------
# define functor to calculate pressure

function (g::Ideal)(V,T)
    P = g.R*T/V
end

function (g::RedlichKwong)(V,T)
    # V : mole volume [m3/kmol]
    # T : temperature [K]
    alf0 = 0.42747*g.R^2*g.Tc^2/g.Pc
    b = 0.08664*g.R*g.Tc/g.Pc
    delta = b
    epsilon = 0
    c = 0
    alf =  alf0 / (T/g.Tc)^0.5
    P = g.R*T/(V-b+c) - alf/(V^2+delta*V+epsilon)
end

function (g::SoaveRedlichKwong)(V,T)
    alf0 = 0.42747*g.R^2*g.Tc^2/g.Pc
    b = 0.08664*g.R*g.Tc/g.Pc
    delta = b
    epsilon = 0
    c = 0
    n = 0.48 + 1.574*g.Ec - 0.176*g.Ec^2
    alf =  alf0 * (1 + n*(1-sqrt(T/g.Tc)) )^2
    P = g.R*T/(V-b+c) - alf/(V^2+delta*V+epsilon)
end

function (g::PengRobinson)(V,T)
    alf0 = 0.457247*g.R^2*g.Tc^2/g.Pc
    b = 0.07780*g.R*g.Tc/g.Pc
    delta = 2*b
    epsilon = -b^2
    c = 0
    n = 0.37464 + 1.54226*g.Ec - 0.26992*g.Ec^2
    alf =  alf0 * (1 + n*(1-sqrt(T/g.Tc)) )^2
    P = g.R*T/(V-b+c) - alf/(V^2+delta*V+epsilon)
end

function (g::AungierRedlichKwong)(V,T)
    alf0 = 0.42747*g.R^2*g.Tc^2/g.Pc
    b = 0.08664*g.R*g.Tc/g.Pc
    delta = b
    epsilon = 0
    c = g.R*g.Tc/(g.Pc+alf0/(g.Vc*(g.Vc+b))) + b - g.Vc
    n = 0.4986 + 1.1735*g.Ec + 0.4754*g.Ec^2
    alf =  alf0 * (T/g.Tc)^(-n)
    P = g.R*T/(V-b+c) - alf/(V^2+delta*V+epsilon)
end

function (g::VanDerWaals)(V,T)
    P = g.R*T/(V-g.b) - g.a/V^2
end

#-------------------------------------------
# auxiliary function to calculate density (applied to all gas type)

function density(g::Gases,V)
    rho = g.MW/V
end

#-------------------------------------------

R  = 8.3145e3 # universal gas constant [J/kmol/K]

MW = 2.01594 # molecular weight [kg/kmol]

Tc = 32.98 # critical temperature [K]

Pc = 1293000 # critical pressure [Pa]

Vc = 0.031846*MW # critical mole volume [m3/kmol]

Ec = -0.217 # eccentricity coef [-]

IdealGas = Ideal(R,MW)

RKGas = RedlichKwong(R,MW,Tc,Pc)

SRKGas = SoaveRedlichKwong(R,MW,Tc,Pc,Ec)

PRGas = PengRobinson(R,MW,Tc,Pc,Ec)

ARKGas = AungierRedlichKwong(R,MW,Tc,Pc,Vc,Ec)

avdw = 24.76e+3 # [Pa.m6/kmol2]
bvdw = 26.61e-3 # [m3/kmol]
VDWGas = VanDerWaals(R,MW,avdw,bvdw)

T = 300

# mole volume list to be checked
Vs = [ 0.05:0.01:0.1;
       0.12:0.02:0.2;
       0.25:0.05:0.4;
       0.5:0.1:1;
       2:2:20 ]

rVs = reverse(Vs)

println("V Ideal RK SRK PR ARK VDW")

#for V in rVs
for V in Vs
    P0 = IdealGas(V,T)
    P1 = RKGas(V,T)
    P2 = SRKGas(V,T)
    P3 = PRGas(V,T)
    P4 = ARKGas(V,T)
    P5 = VDWGas(V,T)
    # density is calculated as ideal gas (in fact, same for all gas type)
    rho = density(IdealGas,V)
#println("$V  $rho  $P1")
println("$V  $P0  $P1  $P2  $P3  $P4  $P5")
#println("$rho  $P0  $P1  $P2  $P3  $P4  $P5")
end

fluentを使った解析

fluentの検証例題VMFL026では、実在気体モデル（ARK）を使い、衝撃波管の解析を行っている。

ここでは、密度モデルとして(1)ARKモデル、(2)Idealモデル、を使った場合、計算結果にどの程度の差異が見られるかを調べた。

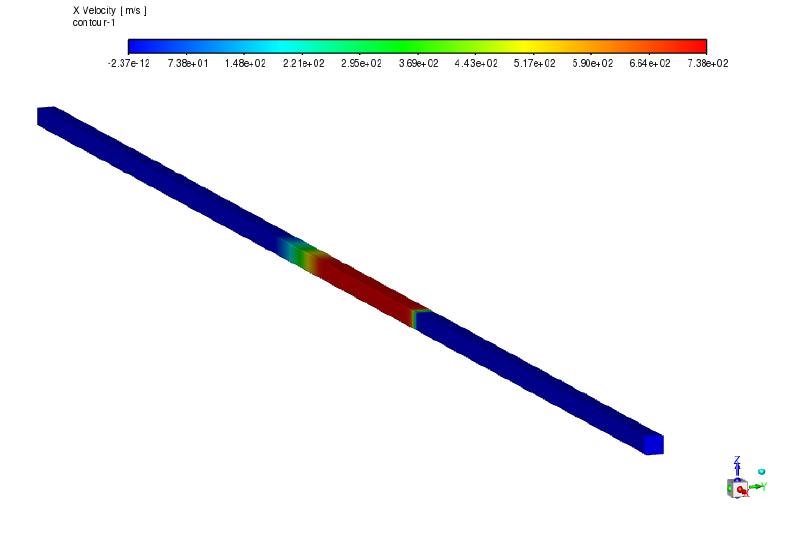
解析領域

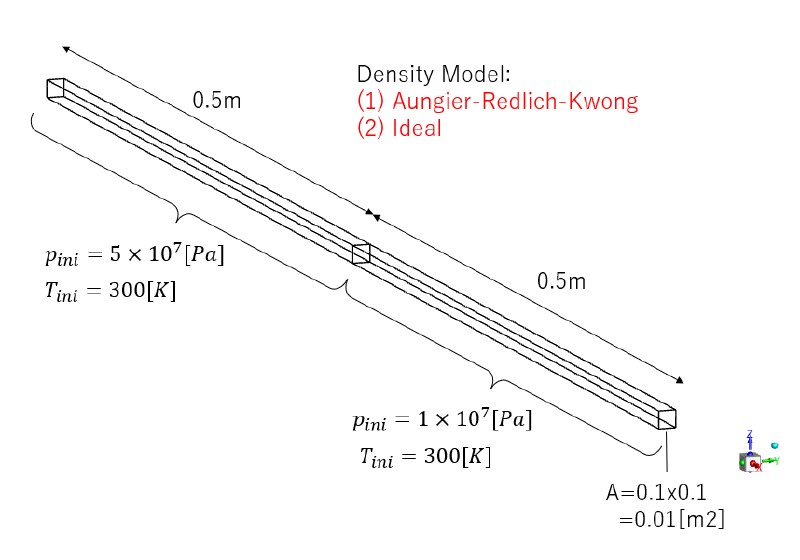
全長1mのダクトの中に水素ガスが充満している。中央部($x=0$)に隔壁があり、初期状態は$x<0$の領域が高圧、$x>0$の領域が低圧となっている。この状態で隔壁をなくした場合の流れの計算を行った。

物性値

ARKモデルで使用した物性パラメータを示す。

property	value	unit	description
R	8.3145e3	[J/kmol/K]	universal gas const
MW	2.01594	[kg/kmol]	molecular weight
Tc	32.98	[K]	critical temperature
Pc	1.293e6	[Pa]	critical pressure
Vc	0.03186*MW	[m3/kmol]	critical mol volume
Ec	-0.217	[-]	eccentricity coef.