滞留時間の計算理論
By M.Sato
概要
空気が建物内部を流動している場合を考える。
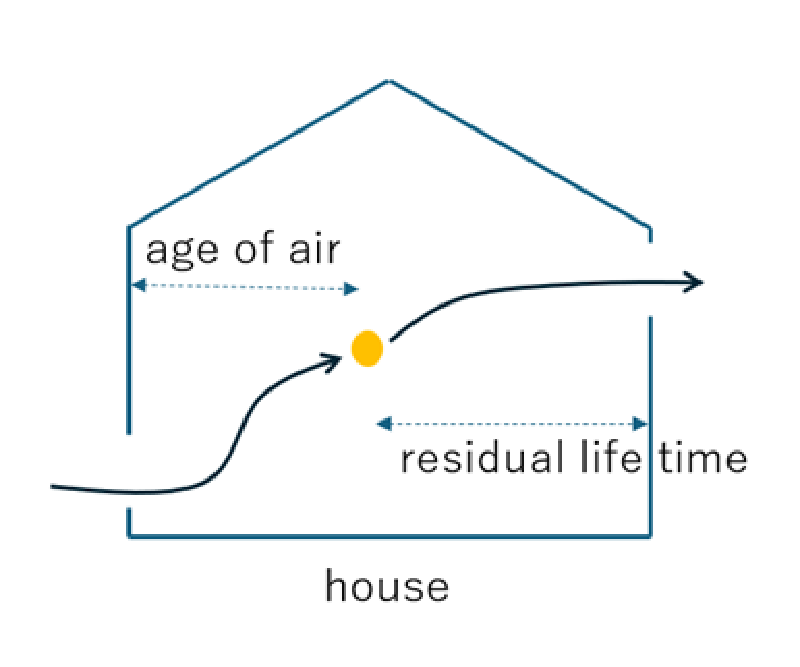
ある流入境界から流入した空気粒子が注目点に到達するまでにかかる時間を空気齢と呼ぶ。
一方その注目点から移動を開始した空気粒子が流出境界から出るまでの時間を空気余命と呼ぶ。
建築関係の分野では、一般に空気齢(age of air)と呼ばれているが、機械関係の分野では空気齢は流体の滞留時間と解釈することもできる。
ここではAnsys Fluentを使って 滞留時間(residence time)を計算するための背景知識を説明し、計算例を紹介する。
滞留時間の計算理論
ここでは流体解析で得られた計算結果から滞留時間を計算する理論を示す。
流体粒子の運動
粒子の運動軌跡に沿って$\frac{d \phi}{d t}=1$という微分方程式を積分する。
この微分方程式は容易に積分でき、$\phi=t+C$という解が得られる。
ここで$t$は流体粒子の運動軌跡に沿った時間、$C$は積分定数であり境界条件から決まる。
流体粒子が解析領域に流入したときに$\phi=0$とすると$C=0$となる。 従って$\phi=t$となり、$\phi$は流体粒子に沿って積分された時間(すなわち滞留時間)になっていることがわかる。
ここで同式を流体解析で使用しているオイラー座標系で記述すると次式が得られる。
$$ \begin{align} \frac{D \phi}{D t}&= \frac{\partial \phi}{\partial t}+u_j \frac{\partial \phi}{\partial x_j}=1 \end{align} $$
ここで$\phi$は滞留時間、$u_j$は$j$方向流速、$x_j$は$j$座標である。 これが滞留時間を計算する方程式になる。
fluentにおけるユーザ定義変数の輸送方程式
fluentのマニュアルによればユーザ定義変数(UDS)の輸送方程式は次式で表される。
$$ \begin{align} \frac{\partial \rho \phi_k}{\partial t} + \frac{\partial }{\partial x_j} \left( \rho u_j \phi_k - \Gamma_k \frac{\partial \phi_k}{\partial x_j}\right) &=S_{\phi_k} \end{align} $$
ここで $k$は複数のUDS変数を区別するための識別番号、$\rho$は流体密度、$\Gamma_k$は拡散係数、$S_{\phi_k}$は生成項である。
以下の説明では、解析対象となるUDS変数は一個のため添字$k$を省略し、また拡散係数がゼロの場合を考えると次式が得られる。
$$ \begin{align} \frac{\partial \rho \phi}{\partial t} + \frac{\partial }{\partial x_j} \left( \rho u_j \phi\right) &=S_{\phi} \end{align} $$
左辺をさらに変形してみると次式が得られる。
$$ \begin{align} &\frac{\partial \rho \phi}{\partial t} + \frac{\partial }{\partial x_j} \left( \rho u_j \phi\right) \\ =& \phi\left( \frac{\partial \rho }{\partial t} + \frac{\partial \rho u_j}{\partial x_j} \right) + \rho\left( \frac{\partial \phi }{\partial t} + u_j \frac{\partial \phi}{\partial x_j}\right) \end{align} $$
質量保存の式より湧き出し吸い込みが無い場合には
$$ \begin{align} \frac{\partial \rho }{\partial t} + \frac{\partial \rho u_j}{\partial x_j} \equiv 0 \end{align} $$
が成り立っており、(5)式第一項は恒等的にゼロである。(5)式第二項は滞留時間の微分方程式(1)より$\rho$である。
これらを(3)式に代入してまとめると最終的に次式が得られる。
$$ \begin{align} S_{\phi}=\rho \end{align} $$
すなわち滞留時間を計算するためにはUDSの生成項$S_\phi$に流体密度$\rho$を指定すればよいことがわかる。
なお上式の誘導において密度の一定性は仮定しておらず、この関係式は非圧縮性流体、圧縮性流体のいずれに対しても有効である。 同様にこの関係式は、定常流れ場、非定常流れ場のいずれに対しても有効である。
fluentを使った解析
非圧縮性流体、圧縮性流体に対して滞留時間を計算した例を示す。
非圧縮性流体
S字形状の流路を対象として計算を行ってみた。
解析モデル
解析モデルを以下に示す。
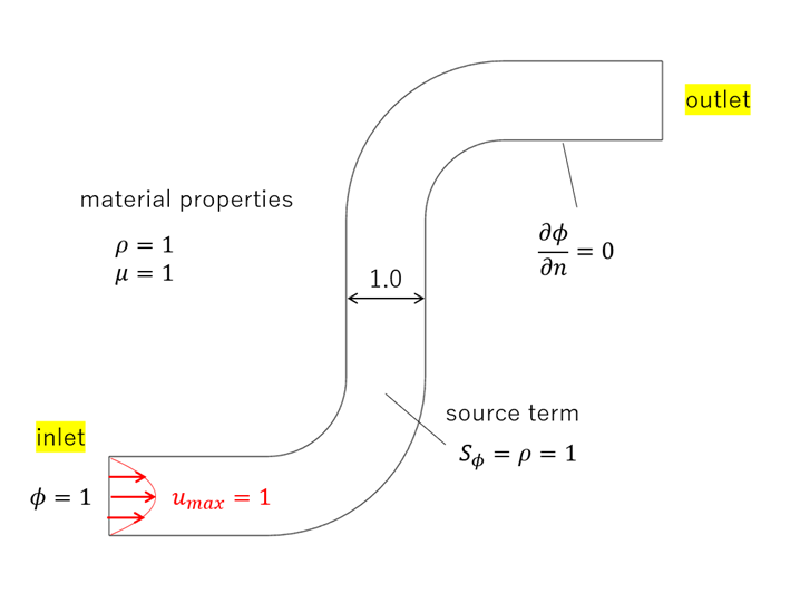
滞留時間は下流に向かって徐々に増加していることがわかる。 各時刻ごとのフロント面(界面)の移動をアニメーションにしてみると以下のようになった。
front
圧縮性流体
亜音速のラバルノズル流れを対象として計算を行ってみた。 元の検証例題はここに説明がある。
解析モデル
以下に解析モデルの模式図を示す。 ここでは亜音速流れを対象とするため、流出境界圧力を$p_e=0.89*p_t=6137[Pa]$とした。
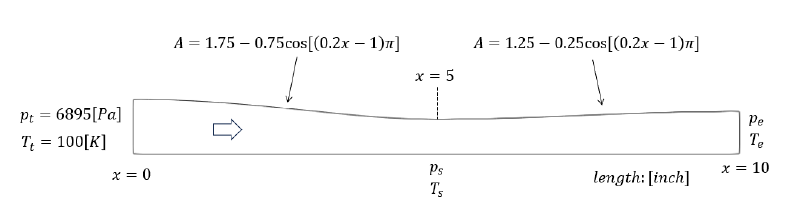
流体は非粘性の空気とし、状態方程式は理想気体とした。
メッシュ分割図を示す。

解析結果
まず最初にいくつかの流れ場の計算結果図を示す。
この流れ場では流路面積が小さくなる部分で流速が増大し、密度が減少していることがわかる。
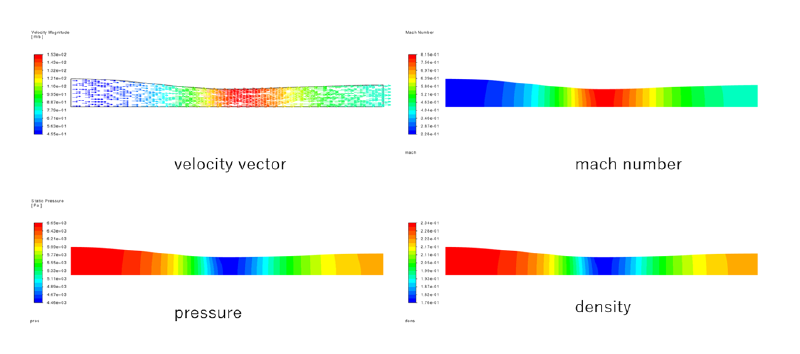
中心軸に沿った軸方向流速(ux)の分布は以下のようになった。
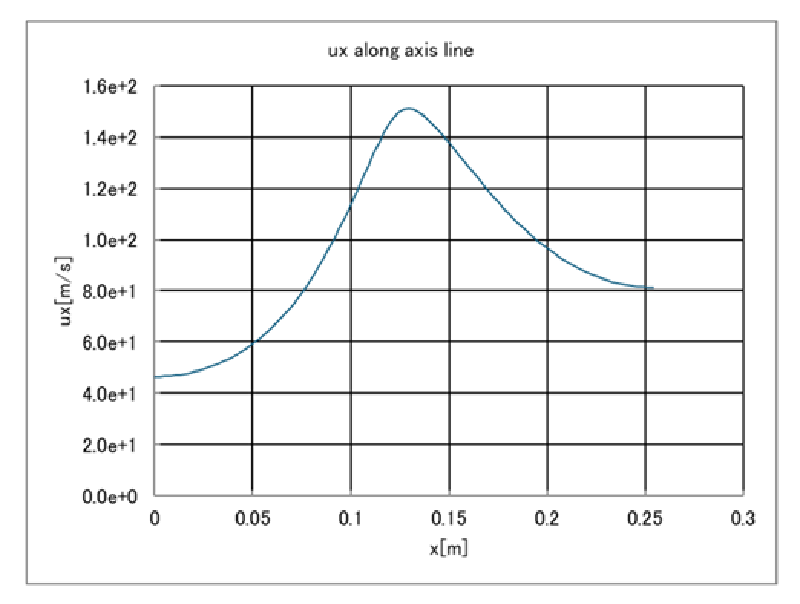
次に、この流れ場を使い、滞留時間の計算を行ってみた。この計算はUDS変数の移流拡散解析である。
密度は空間的に分布する変数となるため以下のユーザ定義関数で指定した。
#include "udf.h"
DEFINE_SOURCE(uds_source,c,t,dS,eqn)
{
return C_R(c,t);
}
以下にUDS(滞留時間)のコンター図を示す。

中心軸上の滞留時間分布
次にこの滞留時間分布が妥当であることを確認するために中心軸上の滞留時間分布を二種類の方法で計算し両者を比較した。
-
流速分布から計算する方法(図中ではvelと表記)
微小区間$dx$を通過するのに必要な時間は$dx/u_x$である。この総和をとることで滞留時間を求めることが可能である。式で記述すると以下のようになる。
$$ \begin{align} ResidenceTime(x)=\int_{x_0}^x \frac{dx}{u_x} \end{align} $$
- 滞留時間(UDS)変数の中心軸上の分布から求める方法(図中ではudsと表記)
これらを図示すると以下のようになった。両者はよく一致していることがわかる。
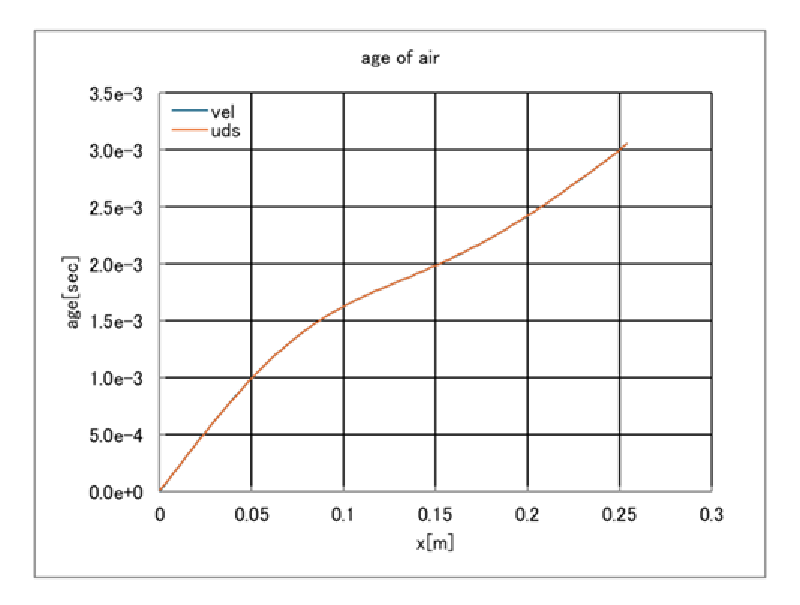
まとめ
流体解析の結果を利用して滞留時間を計算する手法を紹介した。
fluentで計算を行う場合、ユーザ定義変数(UDS)の輸送方程式に流体密度を生成項として指定することで滞留時間を計算できることが分かった。
弊社の解析事例
弊社の流体解析事例については、下記のリンクからご覧ください.