渦輪の解析
By M.Sato
概要
ヘルムホルツの渦定理によれば、完全流体中に発生した渦には以下の特性がある。
- 渦糸に沿ってその強さ(渦度×渦糸断面積)は同じである
- 渦糸は流体中で消滅することはなく、境界部にまで伸びているか閉じたリング状になっているかである
- 渦のない運動は永遠に渦のないままで運動を続ける
リング状になった渦糸は渦輪とも呼ばれており、 渦運動を利用して物質輸送を行うといった応用が考えられている。 また空気砲といった科学おもちゃにも使われている
(参考:空気砲)
ここでは、Ansys Fluentを用いた 数値計算により渦輪のシミュレーションを行ってみた。
解析の方針
- 渦輪は軸対称形状とみなすことができるため、軸対称モデルを使う
- 初期流れ場として、時刻ゼロにおいて瞬間的に渦輪が発生した場合を想定する
- 流体は空気を想定し、非圧縮、等温、層流を仮定する。
初期流れ場の生成
実際の渦輪発生装置は円形の流出口から流体を瞬間的に高速に噴出させるようになっているが、 このような複雑な流れ場では渦輪単独での流動特性を把握するのが難しい。
従ってここでは、瞬間的に渦輪を発生させてその流れ場を初期条件として渦輪の挙動を計算した。
なお初期渦輪は非圧縮性流体の連続方程式を満足するように設定する(ソレノイダル場)。
ストークスの流れ関数
軸対称流れ場では流速をストークスの流れ関数$\Psi$を使って表すことができる。
簡単のため軸方向座標、流速を $x,u$、半径方向座標、流速を$y,v$で表すと流速は次式で表される。
$$ \begin{align} u &= \frac{1}{y}\frac{\partial \Psi}{\partial y} \\ v &= -\frac{1}{y}\frac{\partial \Psi}{\partial x} \end{align} $$
渦度$\omega$は次式で表される。
$$ \begin{align} \omega &= \frac{\partial v}{\partial x}-\frac{\partial u}{\partial y} \\ &= \frac{\partial}{\partial x}\left(-\frac{1}{y}\frac{\partial \Psi}{\partial x}\right)-\frac{\partial}{\partial y}\left(\frac{1}{y}\frac{\partial \Psi}{\partial y}\right) \end{align} $$
従って
$$ \begin{align} \frac{\partial}{\partial x}\left(\frac{1}{y}\frac{\partial \Psi}{\partial x}\right)+\frac{\partial}{\partial y}\left(\frac{1}{y}\frac{\partial \Psi}{\partial y}\right) &= -\omega \end{align} $$
これは、拡散係数を$1/y$にした二次元(軸対称ではない)ポアソン方程式になっている。
流れ関数の計算
$\Psi$を計算するために、まずは二次元モデルを作成した。
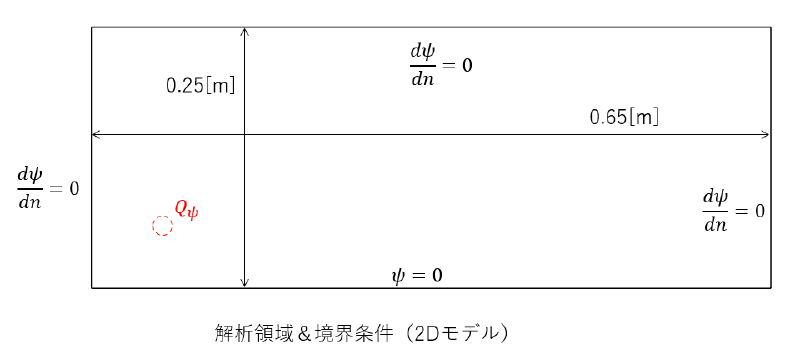
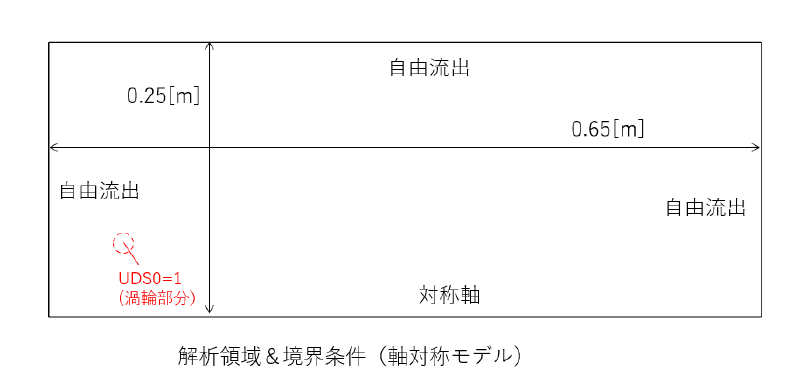
解析対象領域を以下に示す。 $Q_{\Psi}$と書かれた位置に渦管を配置する。
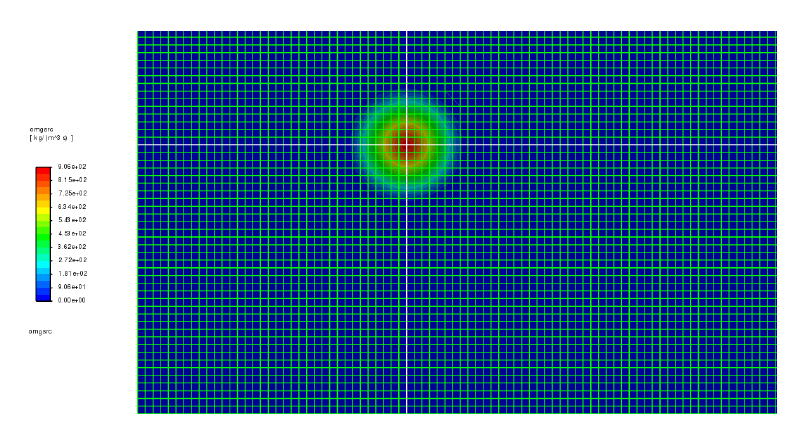
メッシュ分割図を示す。 全領域を1辺2mmの正方形で分割した。
$\Psi$に関するポアソン方程式をfluentを使って計算する。
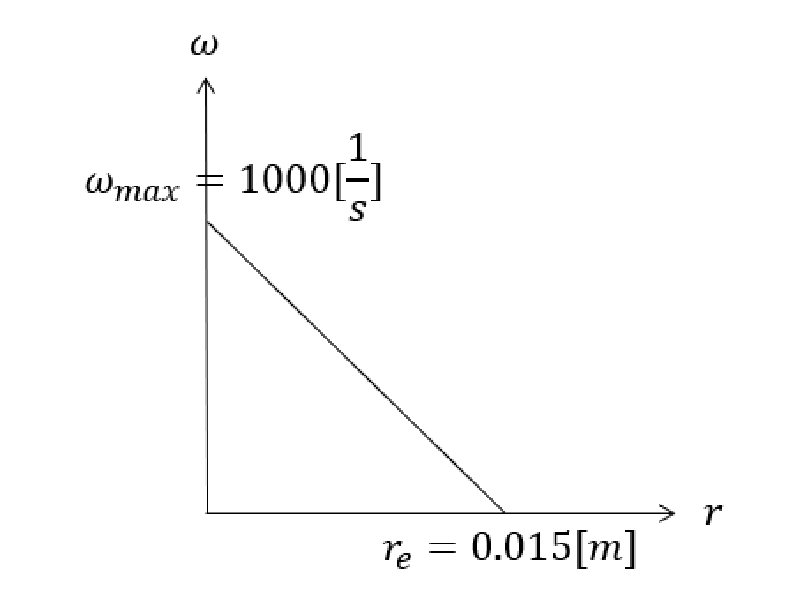
$\omega$(渦度)は、渦輪の部分にだけ分布するようにした。
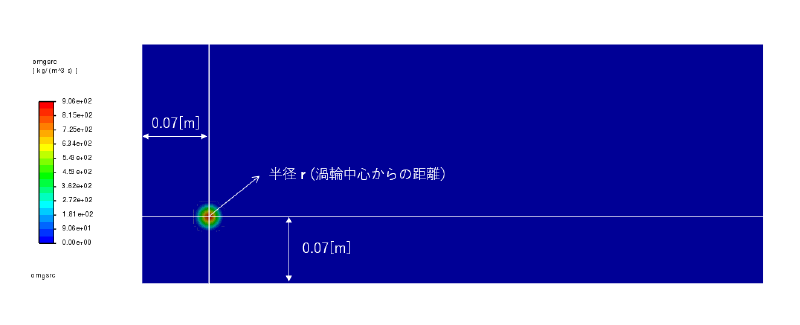
渦管は直径$0.03$[m]であり、渦度は渦管断面中心において最大値$1000$[1/s]となるように設定した。
また渦輪の位置は$x=y=0.07$[m]の位置とした。
ユーザ定義関数の指定
$\Psi$方程式の拡散係数、ソース項をUDFを使い記述した。
また得られた $\Psi$場を空間微分することで流速を計算した。
なお$\Psi$変数は ユーザ定義変数UDS0に割り当てている。
UDFのソースプログラム(fl-vort.c)を示す。
#include "udf.h"
#define RADIMAX 0.015
#define SRCMAX 1000.0
#define XCENTER 0.07
#define YCENTER 0.07
/*-----------------------------------------------------------------*/
DEFINE_DIFFUSIVITY(psidif,c,t,i)
/*-----------------------------------------------------------------*/
{
real xyz[ND_ND];
C_CENTROID(xyz, c, t);
return 1.0/xyz[1];
}
/*-----------------------------------------------------------------*/
DEFINE_SOURCE(psisrc,c,t,dS,eqn)
/*-----------------------------------------------------------------*/
{
real source,radi;
real xyz[ND_ND];
C_CENTROID(xyz, c, t);
radi = sqrt((xyz[0]-XCENTER)*(xyz[0]-XCENTER)
+(xyz[1]-YCENTER)*(xyz[1]-YCENTER));
source = (radi>RADIMAX ? 0.0 : SRCMAX/RADIMAX*(RADIMAX-radi));
dS[eqn] = 0.0;
return source;
}
/*-----------------------------------------------------------------*/
DEFINE_ON_DEMAND(on_demand)
/*-----------------------------------------------------------------*/
{
Domain *d = Get_Domain(1);
Thread *t;
cell_t c;
real xyz[ND_ND];
thread_loop_c (t,d)
{
if (NULL != THREAD_STORAGE(t,SV_UDS_I(0)) &&
NULL != T_STORAGE_R_NV(t,SV_UDSI_G(0)))
{
begin_c_loop (c,t)
{
C_CENTROID(xyz, c, t);
C_U(c,t) = C_UDSI_G(c,t,0)[1]/xyz[1];
C_V(c,t) =-C_UDSI_G(c,t,0)[0]/xyz[1];
}
end_c_loop (c,t)
}
}
}
初期流れ場の計算結果
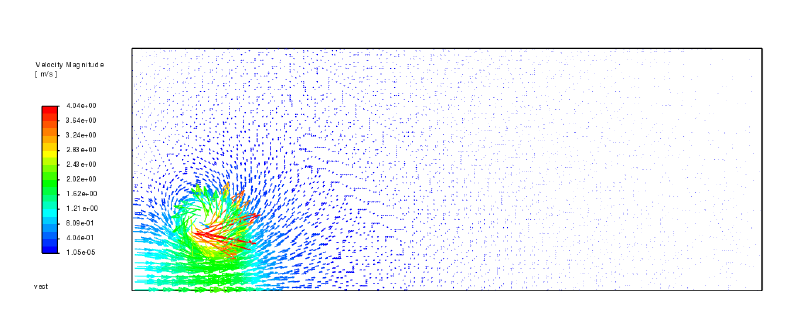
以下に初期流れ場の計算結果を示す。
なおこの計算は流速なしで$\Psi$変数(UDS0)のみの線形解析であり、容易に収束解が得られる。
得られた流れ関数$\Psi$から、UDF内で定義した"on_demand"関数を使い$\Psi$の空間勾配を求め、流速場を計算した。
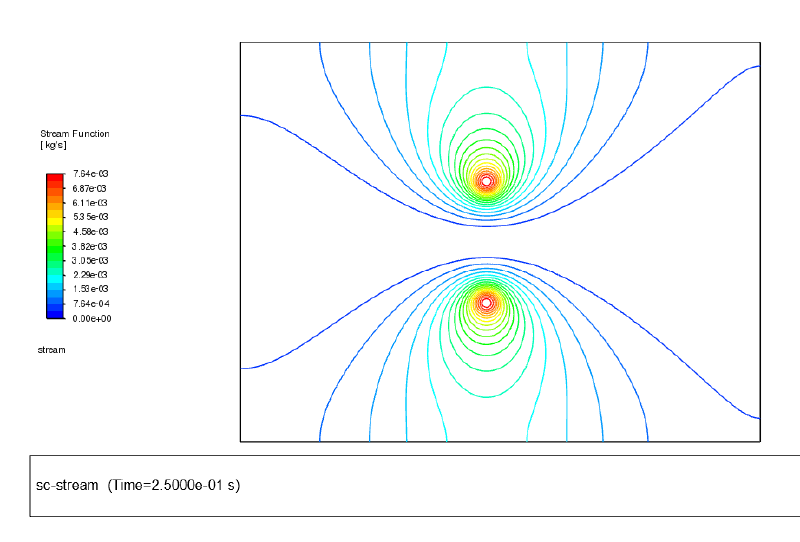
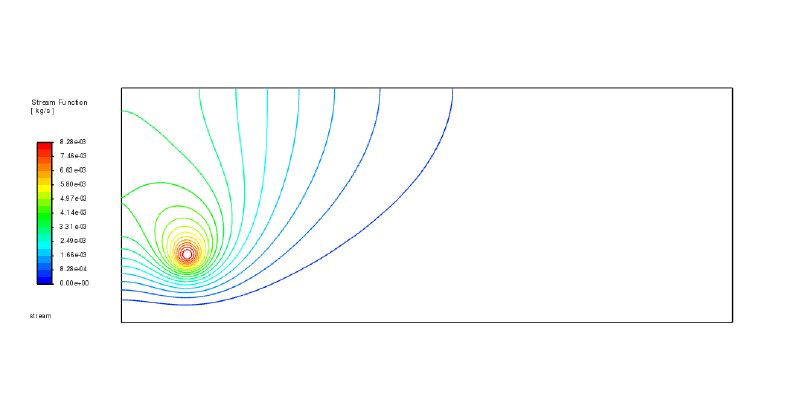 流線(注:これは流速場を軸対称としてポスト処理することで得られる)
流線(注:これは流速場を軸対称としてポスト処理することで得られる)
渦輪の挙動の解析
次に軸対称モデルを使い渦輪の非定常解析を行う。
なおこの解析では渦輪の位置に染料(マーカー)を放出したと仮定し、染料の挙動も同時に計算した。
染料はUDS0変数で表現した。
計算で使用したメッシュ分割は前述のものと同じである。
初期流速
初期流速は前記の流れ関数から計算された値を使用する。
計算モデルが異なるため、fluentのFile → 補間機能を使い流速データを取り込む。
物性値
流体は空気とし、密度$\rho=1.2[kg/m^3]$、粘度$\mu=1.8\times10^{-5}[Pa.s]$とした。
また染料(UDS0変数)の拡散係数はゼロとした。
計算結果
時間刻み幅 $0.0001$秒として$0.5$[sec]まで計算を行った($5000$ステップ)。
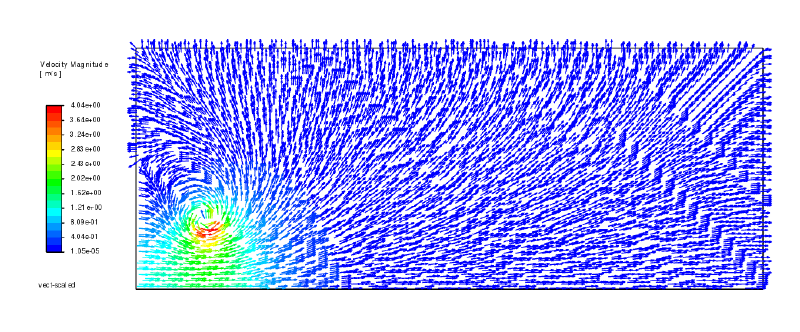
計算結果によれば、渦輪は形状を保持したままで右側に移動していくことがわかった。
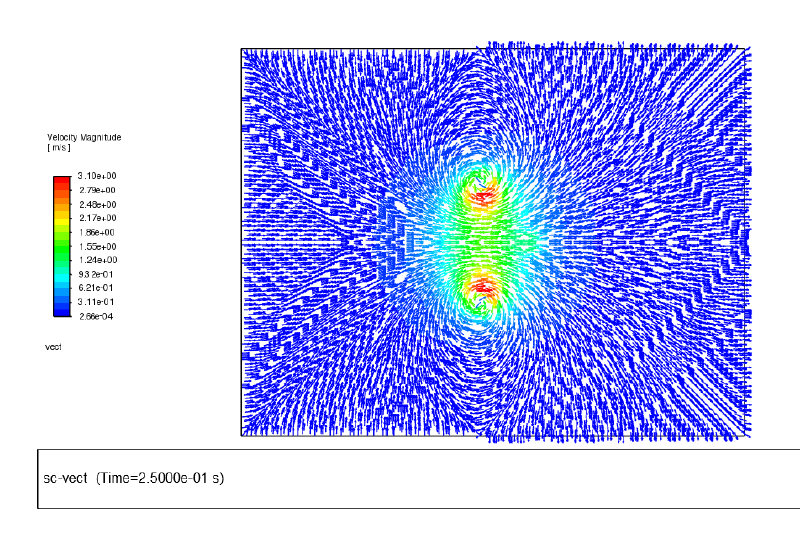
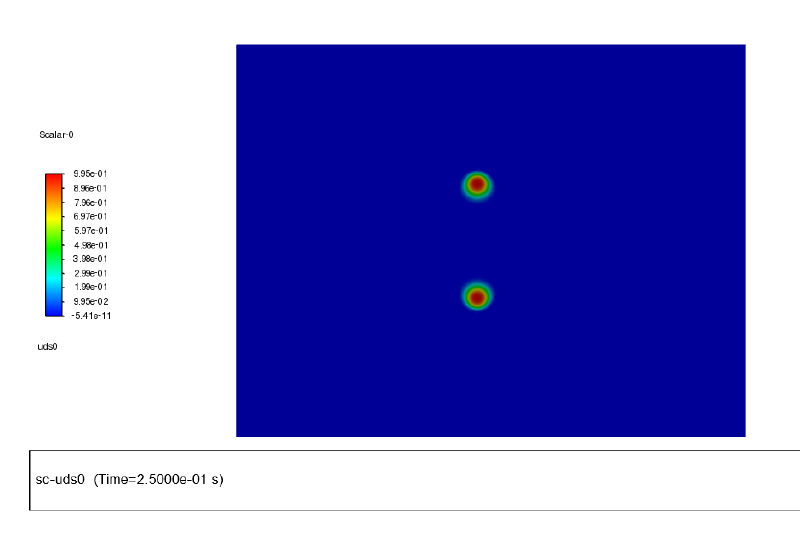
以下に時刻$0.25$秒における計算結果を示す。
なおわかりやすいように対称軸の両側に鏡映反転して結果図を表示している。
アニメーション
いくつかのアニメーションを示す。
流速ベクトル
流線
圧力コンター
渦度コンター
染料濃度(UDS0)コンター
渦輪の移動速度
渦輪の移動速度$V$は次式で近似される。
ここで$\Gamma$は循環、$R$は渦リングの半径、$a$は渦管の半径である。
$$ V = \frac{\Gamma}{4\pi R}\left[ ln\left(\frac{8R}{a}\right)-\frac{1}{4} \right] $$
(参考:渦輪)
ストークスの定理を使うと循環 $\Gamma$は渦度を面積積分することで求めることができる。
初期流れ場のデータを使い実際に計算してみると以下にようになる
$$ \Gamma = \oint \mathbf{u}\cdot d\mathbf{r}=\iint \omega dA=\frac{1}{3}\pi a^2 \omega_{max}=\frac{\pi}{3}(0.015)^2\times 1000=0.2356[m^2/s] $$
これから移動速度を求めると
$$ V = \frac{0.2356}{4\pi \times 0.07}\left[ ln\left(\frac{8\times 0.07}{0.015}\right)-\frac{1}{4} \right] = 0.903 [m/s] $$
一方、時刻0.5[sec]における渦位置を計算結果図から推定すると$x=0.538[m]$程度である。
これから渦の移動速度$V’$を求めると
$$ V’ = \frac{\Delta x}{\Delta t}=\frac{0.538-0.07}{0.5}=0.936 [m/s] $$
これから移動速度 VとV’ はほぼ一致していることがわかった。
まとめ
数値計算により渦輪の挙動を計算してみた。
2次元ポアソン方程式を解くことで渦輪の初期流速場を得ることができた。
また数値計算で得られた渦輪の移動速度は理論式で推定された値とほぼ一致することがわかった。
弊社の解析事例
弊社の流体解析事例については、下記のリンクからご覧ください.