繊維配向テンソルの簡単な計算

はじめに

---

Autodesk Moldflowのような プラスチックの射出成形シミュレーション分野では、 古くから、流速ベクトルから繊維配向を予測することが行われてきました。

一方で繊維補強コンクリートなどは広く普及しているにもかかわらず、 コンクリートのシミュレーション分野では、射出成形シミュレーションで培われた繊維配向の予測技術が、あまり有効活用されていなようにも見えます。

そこで、本記事では、結果の妥当性はさておき、速度ベクトル場から流動中の繊維の再配向を表す2階の配向テンソルを求める方法を紹介します。

流速ベクトル場の計算

---

まず、繊維配向を予測するには流速ベクトル場が必要です。

通常、流速ベクトル場は、流体解析を行えば得られるでしょう。

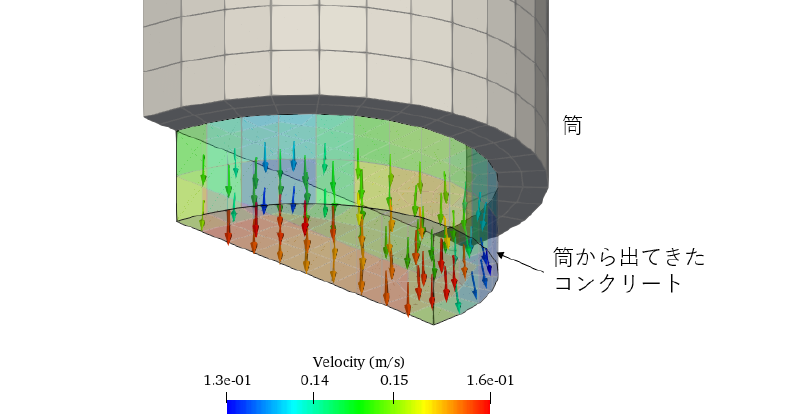
例えば、下図はコンクリートのスランプ試験の解析結果です。

これは、Ansys Fluentで滞留時間に依存して粘性を変えた解析をしており、 ちょうどコンクリートが筒から出てきたところを示しています。 矢印はコンクリートの流速ベクトルを表しています。

流速勾配テンソルの計算

---

次に、流速ベクトルから流速勾配テンソルを求めます。

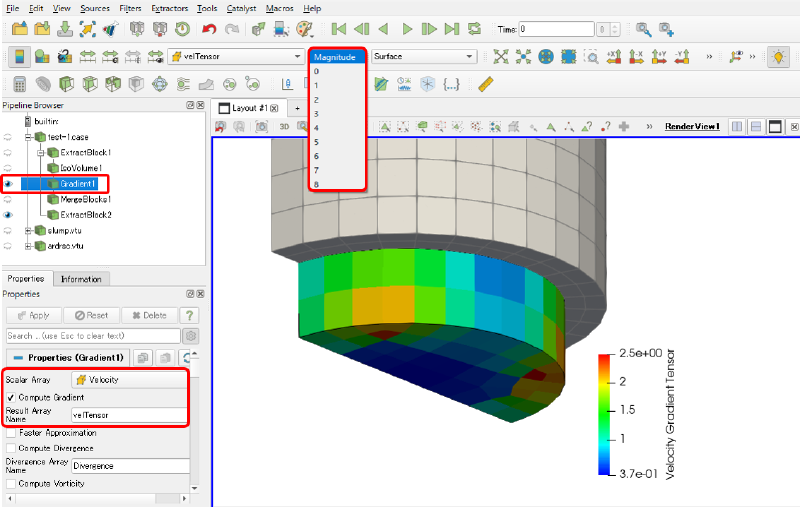
このためには、例えば、ParaViewの勾配計算フィルター(Gradientフィルター)を使うと便利です。
※もちろん、ソルバー自体から直接に流速勾配テンソルを出力した方がより正確かもしれません。

ParaViewのGradientフィルターを適用するには、ParaViewを起動し、流速ベクトルを持ったデータに対して

Filters > Alphabetical > Gradients

からGradientフィルターを起動し、流速ベクトル名の選択などの設定をしてから、Applyします。

結果は、9つの成分(順に、XX, XY, XZ, YX, YY, YZ, ZX, ZY, ZZ)からなるテンソルとなります。

2階の配向テンソルの計算

---

流動中の繊維の再配向は、2階の配向テンソル$\textbf{A}$と4階の配向テンソル$\mathbb{A}$で次式のように表されます。

$$ \textbf{A} = \int_S \textbf{p} \otimes \textbf{p}\ \Psi(\textbf{p}) dp $$

$$ \mathbb{A} = \int_S \textbf{p} \otimes \textbf{p} \otimes \textbf{p} \otimes \textbf{p}\ \Psi(\textbf{p}) dp $$

ここで、$\textbf{p}$は繊維の方向ベクトル、$dp$は単位球面$S:=\lbrace\textbf{p} \in \mathbb{R}^3 : ||\textbf{p}|| = 1\rbrace$の面要素、 $\Psi(\textbf{p})$は繊維配向の分布関数です。

2階の繊維配向テンソルの時間発展方程式は、1922年のJeffryの先駆的な仕事¹に基づいて

$$ \dot{\textbf{A}} = \nabla\textbf{v}\cdot \textbf{A} + \textbf{A}\cdot(\nabla\textbf{v})^T - \mathbb{A} : (\nabla\textbf{v}+(\nabla\textbf{v})^T) $$

のように記述されます。ここで、$\nabla\textbf{v}$は、速度勾配テンソルです。

Jeffryの方程式は、現在まで、様々な改良が加えられていますが、ここでは、 ランダムな繊維の衝突がよりランダムな配向への正味の運動につながるように、配向をより等方的な状態へと向かわせる拡散項を追加した Folgar-Tuckerの発展方程式から、2階の配向テンソルを求めてみます。

しかし、すでに、Fiberoripyのような 便利なライブラリもオープンソースとして存在しますので、これを利用しましょう。

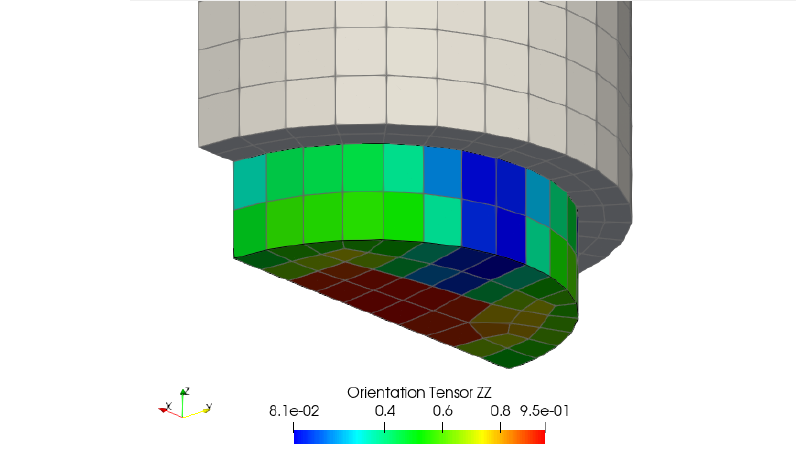
これのexamples内の例を見ながら、Folgar-Tukerの時間発展方程式を、各セルで定常状態になるまで解くと、 下図のように、2階の配向テンソルを得ることができます。

2階の配向テンソルの描画

---

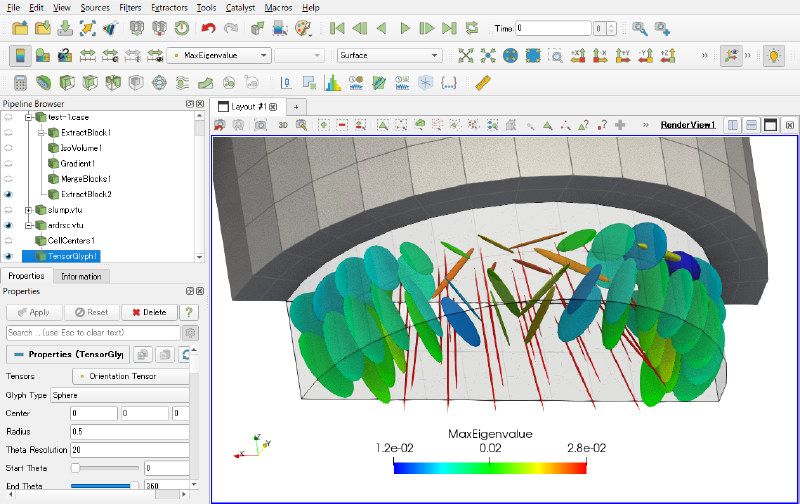
2階の配向テンソルが求まりましたら、これを配向楕円体で描画すると繊維配向の傾向が見やすいでしょう。

このためには、例えば、ParaViewのTensor Glyphフィルターを使用できます。

おわりに

---

繊維補強コンクリートなどのように、繊維配向を知ることが重要な分野において、 射出成形シミュレーションで培われた繊維配向の予測技術があまり使われていない感があります。

そこで今回は、(結果の妥当性はさておき)流速ベクトル場から配向テンソルを容易に計算できることを紹介しました。 今後は、実際に、さまざまな分野で、この知見を有効活用できたらなあと思います。

• orientation tensor
• Moldflow
• ParaView