Fluid Analysis流体解析

事例詳細/サイクロンセパレータ

サイクロンセパレータ内部の粒子分離過程をDPM法で解析します。レイノルズ応力輸送方程式モデルを用いて、粒径による分離特性の違いを詳細に評価し、装置性能の最適化を支援します。

サイクロンセパレータの粒子分離原理 入口 含塵空気 外側下降流 内側上昇流 大粒径→外壁→下部へ 小粒径→中心→上昇 清浄空気出口 小粒径粒子含む 粒子排出口 大粒径粒子 分離メカニズム 大粒径：遠心力大 小粒径：流体追従 外側下降流 内側上昇流 遠心力 > 流体抵抗 → 大粒径が分離 旋回流による遠心力で粒子を粒径別に分離

サイクロンセパレータ内部の空気流れにおける粒子の分離過程の把握

概要

サイクロンセパレータとは流体中に混在している粒子を分離するための装置です。粒子を大きさ毎に正確に分離することは困難ですが、低コストであり可動部がなく保守が容易であることから、正確な粒子分離の前処理として産業界で広く使用されています。

ここでは典型的なLapple型サイクロンセパレータを対象として装置内の流れの様子を解析してみました。解析の結果、流れ場の特性（速度分布、圧力分布等）、および粒径の違いによる挙動を把握することが出来ました。これらの結果により装置の改善指針を得ることが出来ます。

解析手法

空気流れをナビエストークス式（オイラー座標系）で計算し、粒子はラグランジュ座標系で追跡する方法を使用しました。空気に対する粒子の影響はナビエストークス式中のソース項として表されます。

DPM（Discrete Phase Model）法

この計算手法はDPM（discrete phase model）法と呼ばれています。

サイクロンセパレータのような強い旋回を伴う流れでは、渦粘度を定数として扱う乱流モデルは不適切であり、レイノルズ応力の非等方性を考慮することが必要です。ここでは以下に示すレイノルズ応力輸送方程式モデルに基づき計算を行いました。

DPM法：オイラー・ラグランジュ連成解析 連続相（空気流れ）- オイラー座標系 ナビエ・ストークス式で計算 格子点での速度・圧力計算 流体力 反力 分散相（粒子）- ラグランジュ座標系 個々の粒子を追跡 粒子の運動方程式 m_p dv_p/dt = F_drag + F_gravity + ... 抗力、重力、遠心力、その他の力 流体と粒子の相互作用を考慮した連成解析手法

レイノルズ応力輸送方程式モデル

$$\frac{\partial}{\partial t}\left(\rho \overline{u_i'u_j'}\right) + \frac{\partial}{\partial x_k}\left(\rho_k \overline{u_i'u_j'}\right) = D_{ij} + P_{ij} + \Pi_{ij} + \varepsilon_{ij}$$

ここで

応力拡散項: \(D_{ij}\)

$$D_{ij} = -\frac{\partial}{\partial x_k}\left[\rho \overline{u_k'u_i'u_j'} + \overline{p'\left(\overline{u_i'}\delta_{jk} + \overline{u_j'}\delta_{ik}\right)}\right] - \mu\left(\frac{\partial}{\partial x_k}\overline{u_j'u_k'}\right)$$

せん断生成項: \(P_{ij}\)

$$P_{ij} = -\rho\left[\overline{u_i'u_k'}\frac{\partial u_j}{\partial x_k} + \overline{u_j'u_k'}\frac{\partial u_i}{\partial x_k}\right]$$

圧力ひずみ項: \(\Pi_{ij}\)

$$\Pi_{ij} = -\rho\left(\frac{\partial \overline{u_i'}}{\partial x_j} + \frac{\partial \overline{u_j'}}{\partial x_i}\right)$$

散逸項: \(\varepsilon_{ij}\)

$$\varepsilon_{ij} = -2\mu\frac{\overline{\partial u_i'}}{\partial x_k}\frac{\overline{\partial u_j'}}{\partial x_k}$$

解析条件

一般的に粒子は様々な粒径のものが含まれていますが、ここでは粒径の分布はrosin-rammler分布に従うとしました。この分布は下式で表されます。

$$Y_d = e^{-(d/\bar{d})^n}$$

Rosin-Rammler分布式

ここで

  • • \(Y_d\): \(d\)より大きい粒子の質量分率
  • • \(d\): 粒子の直径
  • • \(\bar{d}\): 平均径
  • • \(n\): スプレッドパラメータ

解析パラメータ

  • 最小粒径：1[μm]
  • 最大粒径：100[μm]
  • 平均粒径：10[μm]
  • スプレッドパラメータ：n=3.5
  • 粒径分割数：10個（粒子を粒径に応じて10種類に分級）
  • 流入速度：20[m/s]

解析結果

解析モデル

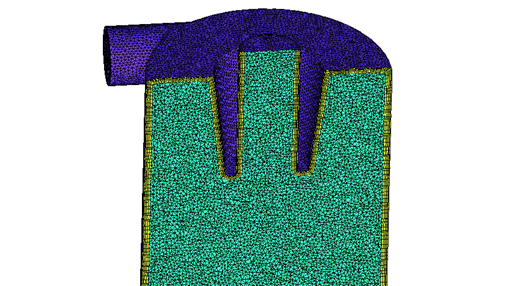
解析に使用したモデルを以下に示します。

サイクロンセパレータの解析モデル
解析モデル　上部メッシュ断面図
ANSYS CFD PrepPostにて作成
メッシュ構造
要素種類: Tetra/Prism

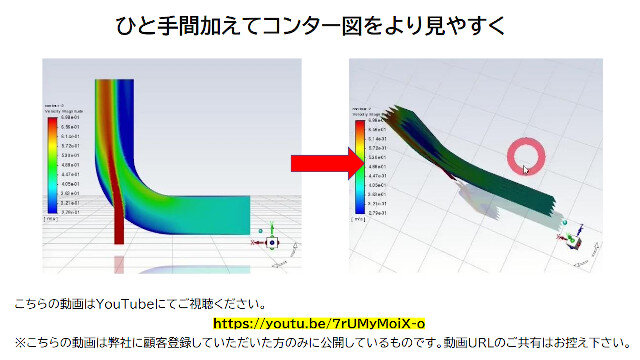
流れ場の特性

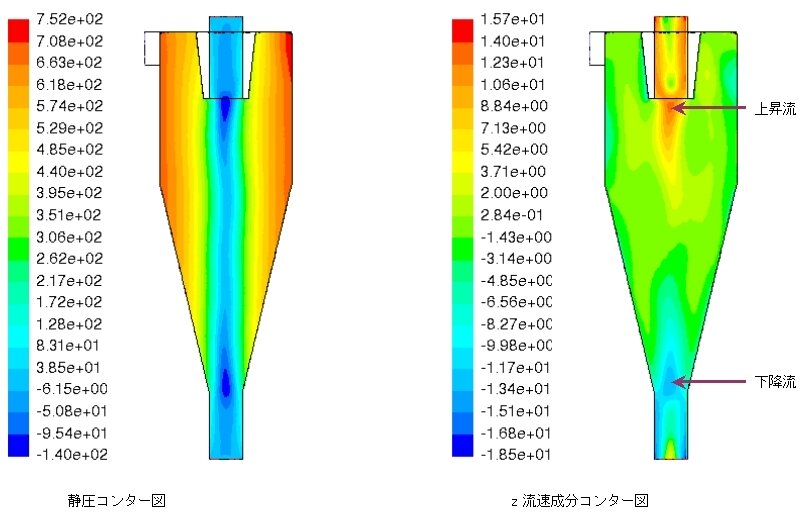
以下の、サイクロンの鉛直断面における静圧コンター図を見ると遠心力のため中心軸付近で圧力が低くなっており、周囲壁面で圧力が高くなっていることが分かります。

また、サイクロン中心軸付近のz方向（軸方向）流速成分コンター図を見ると、サイクロンの上部では上昇流、下部では下降流が生じていることが分かります。

サイクロン内の圧力・流速分布
サイクロン内の静圧分布と軸方向流速分布

粒径による分離特性の違い

次に粒径が異なる場合の典型的な粒子の挙動を示します。

粒径による挙動の違い

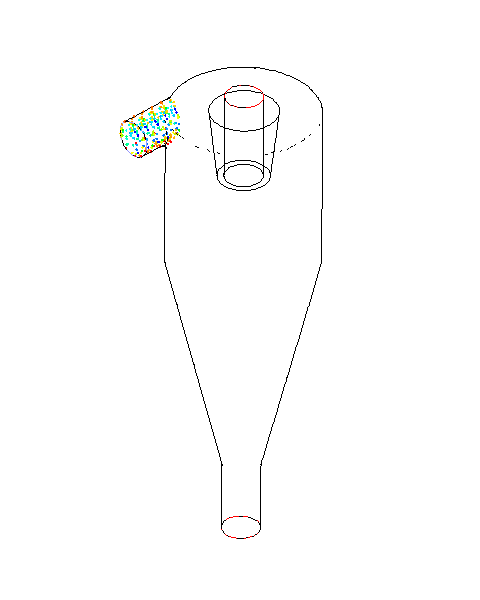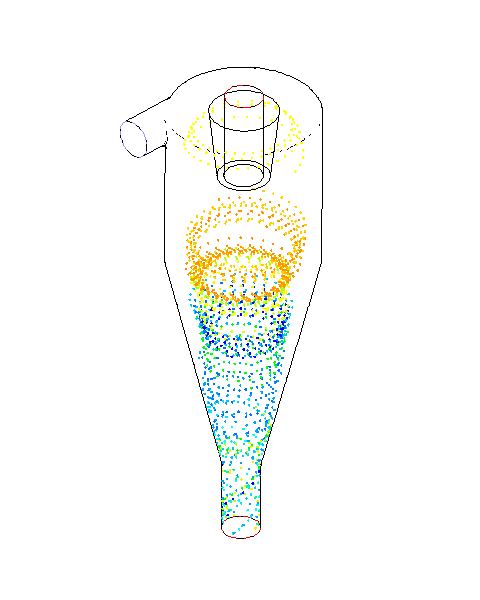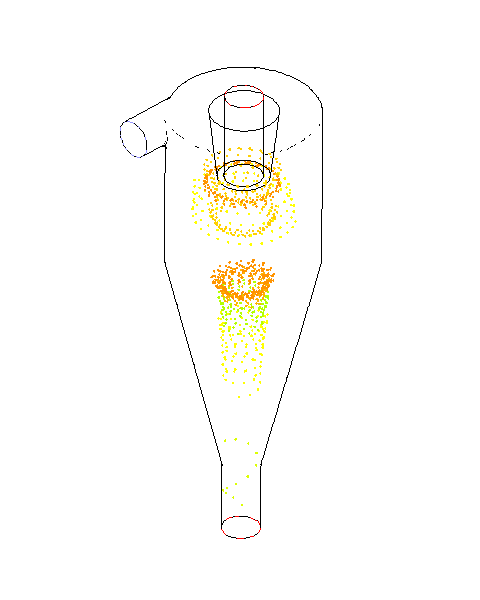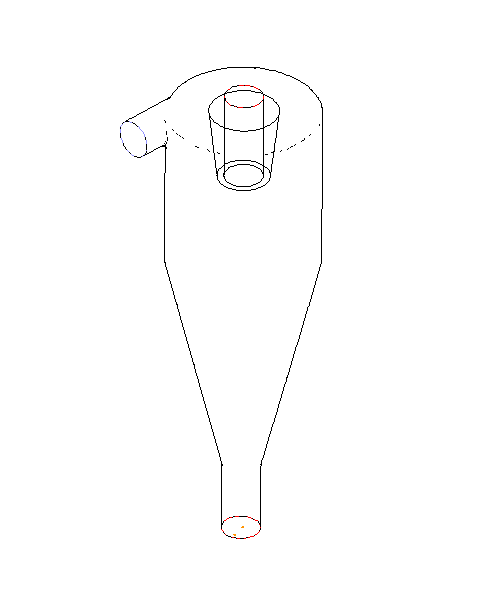
  • 小粒径粒子：上方の流出口から排出される
  • 大粒径粒子：サイクロンの外壁に沿って旋回し、装置内で滞留する傾向
  • 力の釣り合い：遠心力、壁面からの反力、重力が釣り合うため

このような粒子の挙動は現実のサイクロンでも観察されています。

最後に上記左端の粒径1[μm]のケースのアニメーションを以下に示します。

粒径1μmの粒子挙動アニメーション
粒径1[μm]の粒子の挙動（上方流出口への排出パターン）

解析から分かること

解析から得られた知見

  • DPM法の有効性：オイラー・ラグランジュ座標系による効率的な粒子追跡
  • レイノルズ応力モデル：旋回流における非等方性乱流の正確な評価
  • 粒径分布の影響：Rosin-Rammler分布による実用的な分離特性予測
  • 分離効率の最適化：圧力分布と流速分布から装置形状の改善指針を導出
  • 実証性の確保：現実の装置挙動との高い一致性を確認
サイクロンセパレータDPM解析プロセス 1. モデル作成 ・形状定義 ・メッシュ生成 ・境界条件設定 ・粒径分布設定 1 2. 流れ場計算 ・Reynolds応力 ・圧力分布 ・速度分布 ・旋回流計算 2 3. 粒子追跡 ・DPM法適用 ・粒子軌跡計算 ・遠心力評価 ・分離過程評価 3 4. 性能評価・最適化 ✓ 分離効率分析 ✓ 粒径別挙動評価 ✓ 圧力損失評価 ✓ 装置形状最適化 高精度な粒子追跡により分離性能を詳細に評価・最適化

流体解析・ソフトウェア お問い合わせ

ご相談・ご質問、技術的なご質問、お見積り依頼（年度内※急ぎ、来年度予算）など、下記よりお問合せください。

サイクロンセパレータのDPM解析により、粒子分離効率の向上と装置設計の最適化をサポートいたします。

関連資料ダウンロード

(初心者向け)【動画】コンター図をより見やすく

(初心者向け)【動画】コンター図をより見やすく

コンター図はAnsys Fluentでデフォルトとして出力されます。
しかしながら、場合によっては出力凡例の範囲を任意に変更したり、表示方法の工夫を要する場合があります。
本資料では、出力凡例の変更や、3次元系での任意断面出力の設定方法をご覧いただけます。

※こちらの資料は動画です。PDF内のURLからYouTubeにアクセスしてご視聴ください。
Ansys Fluent 2023R1アップデート内容のご紹介

Ansys Fluent 2023R1アップデート内容のご紹介

Ansys Fluent 2023R1のアップデート内容を紹介した資料です。
室内の湿分吸着シミュレーション

室内の湿分吸着シミュレーション

この資料では、密閉された室内で加湿器から室内に拡散された水蒸気が吸湿される様子をシミュレートする方法について解説しております。
PyFluent入門 ～ インストールから例題まで ～

PyFluent入門 ～ インストールから例題まで ～

Ansys Fluentには新機能としてPyFluentが実装されました。この資料ではPyFluentをインストールして計算するまでの流れを説明しております。資料内で使用している例題が欲しい方はその旨をお問い合わせ下さい。
AnsysFluent2025R2アップデート内容のご紹介

AnsysFluent2025R2アップデート内容のご紹介

AnsysFluentの2025R2の新機能紹介資料です。
※PDF資料のため動画が画像になっている箇所があります。完全な資料をお求めの方は弊社までお問い合わせ下さい。
AnsysFluent2023R2アップデート内容のご紹介

AnsysFluent2023R2アップデート内容のご紹介

AnsysFluentの2023R2での新機能の紹介資料です。
※PDF資料のため動画が画像になっている箇所があります。完全な資料をお求めの方は弊社までお問い合わせ下さい。
AnsysFluent2024R1アップデート内容のご紹介

AnsysFluent2024R1アップデート内容のご紹介

AnsysFluentの2024R1での新機能の紹介資料です。
※PDF資料のため動画が画像になっている箇所があります。完全な資料をお求めの方は弊社までお問い合わせ下さい。
OpenFOAMによるセミサブ型浮体周りの作用力の数値シミュレーション

OpenFOAMによるセミサブ型浮体周りの作用力の数値シミュレーション

構造強度や発電効率にも影響する流体力をOpenFOAMを用いた3D数値シミュレーションで評価しました
Canteraによるバーナー火炎問題の計算

Canteraによるバーナー火炎問題の計算

この資料では、オープンソースアプリであるCanteraを使って例題の一つであるバーナー火炎問題を計算する方法について解説しています。
ダイナミックメッシュと６自由度ソルバーによるシミュレーション

ダイナミックメッシュと６自由度ソルバーによるシミュレーション

本資料では、ダイナミックメッシュと６自由度ソルバーを使って２次元翼にかかる揚力をシミュレーションする方法について解説します。
お問い合わせ
JKA Social Action 競輪とオートレースの補助事業 FEMAP NX ASTEA MACS Ver.12 3次元温度応力解析 MECHANICAL FINDER 有限要素法による骨強度解析ソフト