事例詳細/オイルダンパー

オイルダンパー内部のオリフィス付近の流体解析を数値シミュレーションで実施します。異なる粘度条件での流動パターンと抗力特性を比較し、ダンパー性能の最適化を支援します。

オイルダンパーの構造と作動原理：オリフィスの往復運動による減衰効果

ダンパー内部オリフィス付近の流体解析

概要

オイルダンパーは車両や機器の振動減衰を目的に用いられる装置です。身近なところでは、開閉式ドアの動きを滑らかにするために取り付けられています。

そのダンパー内部構造を簡単化（二次元モデル）して、閉じた円筒容器中を往復運動するオリフィスに働く流体力と流動パターンを調べました。動作流体の粘度は、水の様な低粘度流体（1mPa·s）とオイルを想定して水の１０００倍（1Pa·s）の場合で比較しました。

粘性支配と慣性支配の流れパターン比較：低粘度では乱流的、高粘度では層流的

解析理論

オリフィスが速度vで移動しているとき、抵抗力（Ｆ）は、概ね

$$F = \alpha v + \frac{1}{2}\beta v^2$$

抵抗力の基本式

です。1次の項が粘性による寄与分、2次の項が慣性効果です。この問題では、オリフィスを角周波数（ω）、振幅（Α）で正弦波的に振幅させています。

したがって、オリフィスの位置（x）と速度は、各々

$$\begin{aligned} x &= A \sin(\omega t) \\ v &= A\omega \cos(\omega t) \end{aligned}$$

オリフィスの位置と速度の時間変化

t:時間となります。正弦波的な運動により、粘性支配と慣性支配の流れの違いを明確に評価できます。

解析結果

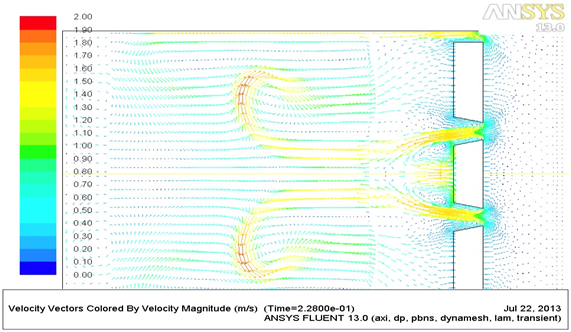
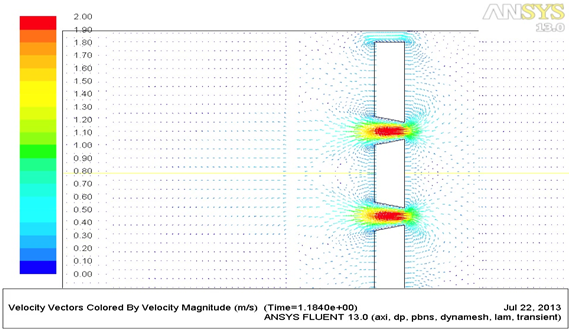
流速ベクトル分布の比較

異なる粘度条件でのオリフィス周辺の流速ベクトル分布を比較します。

粘度：水の1000倍の流速ベクトル図 — 粘度：水の1000倍（1Pa·s）流速ベクトル図

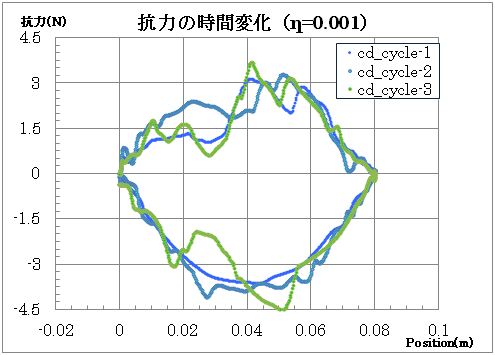
抗力の時間変化

異なる粘度条件での抗力の時間変化特性を比較します。粘度の違いによる動的応答の変化が確認できます。

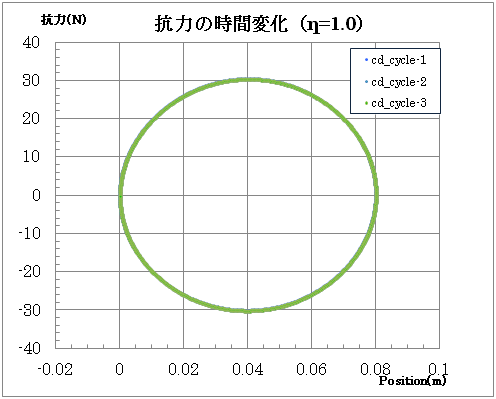
粘度：水の1000倍の抗力時間変化 — 粘度：水の1000倍（1Pa·s）抗力の時間変化

理論的考察

粘度が大きく、慣性項が無視できる場合、

$$\begin{aligned} F &= \alpha v \propto \cos(\omega t) \\ x &= A \sin(\omega t) \end{aligned}$$

粘性支配時の関係式

と、なるので時々刻々変動するFとxを縦軸、横軸にとってプロットすると、楕円上の軌跡を描きます。

今回の解析結果では、動作液体が水の1000倍（1Pa·s）程度の粘度の際、上記の様な状態が実現することが分かりました。実際の流体の流れは複雑で、慣性の影響は速度の2次の項（角周波数2ω）だけではありませんが、流体の粘度を下げると、縦軸：F、横軸：xの軌跡が楕円からズレ、周期毎に軌跡が変化して同じ軌跡を辿ることの無いカオス（乱流）的な状態に至ることが計算結果から示されました。